НАУЧНО - ПОПУЛАРНИ СТАТИИСе залагаме за зголемување на свеста за местото и улогата на математиката во науките, технологијата, наставата, природата и културата.
|
боење графови
Графовите се многу практичен математички модел и се користат во разни области од науката и човековата дејност. Со помош на графови можат да се претстават мрежи од места и патишта што ги поврзуваат, структурни формули на хемиските соединенија, луѓе и релации меѓу нив и слично. Ги разгледуваме законитостите за боење на планарни графови и даваме конкретен пример за боење на картата на Скопје во четири бои.
Граф е апстрактен математички поим и претставува колекција од точки и линии коишто сврзуваат некое (можно е и празно) подмножество од тие точки. Точките од графот најчесто се викаат темиња, но се викаат и јазли или просто точки. Линиите што ги сврзуваат темињата на графот најчесто се викаат ребра, но се викаат и лаци или линии. Ако множеството X е множеството од темиња на графот, а U е множеството од ребра, тогаш секој елемент од множеството од ребра можеме да го запишеме како пар (x,y), каде што x,y се се елементи од X. Во зависност од тоа дали сите парови што го формираат множестовто U се подредени или не, разликуваме ориентиран, односно неориентиран граф.
Граф е апстрактен математички поим и претставува колекција од точки и линии коишто сврзуваат некое (можно е и празно) подмножество од тие точки. Точките од графот најчесто се викаат темиња, но се викаат и јазли или просто точки. Линиите што ги сврзуваат темињата на графот најчесто се викаат ребра, но се викаат и лаци или линии. Ако множеството X е множеството од темиња на графот, а U е множеството од ребра, тогаш секој елемент од множеството од ребра можеме да го запишеме како пар (x,y), каде што x,y се се елементи од X. Во зависност од тоа дали сите парови што го формираат множестовто U се подредени или не, разликуваме ориентиран, односно неориентиран граф.
|
Неориентиран граф е подреден пар G=(X,U) што се состои од конечно непразно множество X и едно зададено множество U од двоелементни подмножества од X. Елементите на X се нарекуваат темиња на графот и најчесто ги означуваме со букви: x,y,z и така натаму. Елементите на U ги нарекуваме ребра на графот и се означуваат со (x,y) или xy што претставува ребро кое ги поврзува темињата x и y. Притоа, за темињата x и y велиме дека се соседни. Графот е неориентиран ако релацијата за соседност е симетрична. Ако ребрата u и v имаат заедничко теме, велиме дека се соседни ребра. Графот до p темиња и q ребра го викаме (p,q) граф. Графот (1,0), составен од една точка, се вика тривијален граф.
|
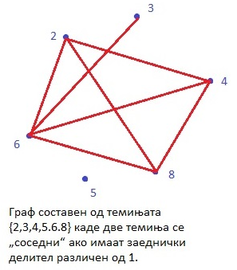
Степен на темето x во графот G=(X,U) е бројот на ребра кои се инцидентни со x (соседни со заедничко теме x) во G. Ознака: deg(x). На пример, во горниот граф чии темиња се {2,3,4,5,6,8}, deg(6)=4, deg(5)=0, deg(8)=3, deg(4)=3, deg(3)=1, deg(2)=3. Со d(G) го означуваме најголемиот степен на теме во графот G.
Теорема 1. Збирот на степените на сите темиња во графот G=(X,U) со p темиња и q ребра, е еднаков на удвоениот број од бројот на ребра на графот.
Графот во кој сите темиња имаат еднаков степен m се вика регуларен граф од степен m. Графот G со p темиња е комплетен ако секое негово теме има степен p-1. Според Теоремата 1, следува дека бројот на ребра во комплетниот граф со p темиња изнесува q=p(p-1)/2.
Маршрута во графот G=(X,U) е конечна наизменична низа од темиња и ребра x0, u1, x1, u2, … , un, xn, која почнува и завршува со теме. За бројот n велиме дека е должина на маршуртата. Маршрутата е затворена ако x0=xn. Маршрутата е верига ако ниту едно ребро не се повторува два или повеќе пати во низата x0, u1, x1, u2, … , un, xn. Маршрутата е пат ако ниту едно теме не се повторува два или повеќе пати во низата x0, u1, x1, u2, … , un, xn. Маршрутата е циклус ако е затворена верига. Маршрутата е контура (циклус) ако е затворена и ниедно теме не се повторува два или повеќе пати во низата x0, u1, x1, u2, … , un, xn, освен што x0=xn.
За графот G=(X,U) велиме дека е бипартитен (дводелен) ако множеството темиња може да се разбие на две непразни дисјунктни подмножества X1 и X2, така што за секое ребро (x,y) од G да важи x припаѓа на X1, y да припаѓа на X2.
За едно подмножество темиња S од графот G=(X,U) велиме дека е внатрешно стабилно ако пресекот на U(S) и S е празно можество, при што U(S) е унија од сите множества U(x) (x\in S), a U(x)={y|y\in X & (x,y)\in U}. Со други зборови, ниту еден пар различни темиња од S не се меѓусебно соседни во G. Со Ф ја означуваме фамилијата од сите внатрешно стабилни подмножества темиња на графот G=(X,U). Број на внатрешна стабилност на графот G е бројот а(G)=max|S|, S \in Ф.
Правилно обојување на граф е придружување бои на темињата на графот, при што ниеден пар соседни темиња не добиваат иста боја. Графот се нарекува n-обојлив ако неговите темиња може да се обојат со n бои. Хроматски број h(G) на графот G=(X,U) е најмалиот број бои со кои графот може правилно да се обои.
Теорема 2. За бројот на внатрешна стабилност a(G) и хроматскиот број k(G) на графот G со p темиња важи a(G)h(G) >= p.
Теорема 3. (Теорема на König) Графот е бихроматски (има хроматски број 2) ако и само ако е бипартитен.
Условот графот да биде бипартитен е еквивалентен со тоа G да не содржи контури со непарна должина.
Последица. Хроматскиот број на еден граф G е поголем или еднаков на 3 ако и само ако G има непарен циклус.
Теорема 4. За секој сврзан граф G важи дека h(G) е помал или еднаков на d(G)+1.
Теорема 5. (Теорема на Brooks) За хроматскиот број на сврзаниот граф G кој не е комплетен и кој не е непарен циклус важи h(G) <= d(G).
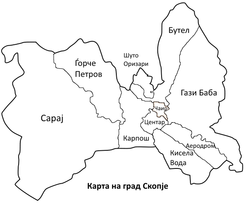
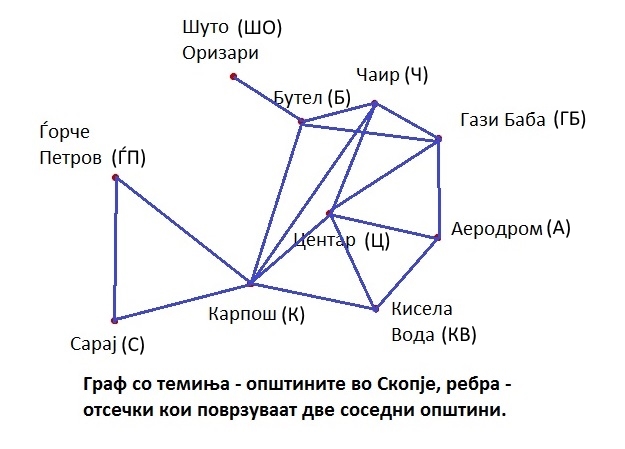
Во следниот пример, теоремата на Brooks е употребена за полесно наоѓање на хроматскиот број на графот чиј темиња се општините на градот Скопје, а рабови се отсечките кои поврзуваат темиња на две соседни општини.
Графот G кој е добиен на овој начин има 10 темиња и 16 рабови.
Теорема 1. Збирот на степените на сите темиња во графот G=(X,U) со p темиња и q ребра, е еднаков на удвоениот број од бројот на ребра на графот.
Графот во кој сите темиња имаат еднаков степен m се вика регуларен граф од степен m. Графот G со p темиња е комплетен ако секое негово теме има степен p-1. Според Теоремата 1, следува дека бројот на ребра во комплетниот граф со p темиња изнесува q=p(p-1)/2.
Маршрута во графот G=(X,U) е конечна наизменична низа од темиња и ребра x0, u1, x1, u2, … , un, xn, која почнува и завршува со теме. За бројот n велиме дека е должина на маршуртата. Маршрутата е затворена ако x0=xn. Маршрутата е верига ако ниту едно ребро не се повторува два или повеќе пати во низата x0, u1, x1, u2, … , un, xn. Маршрутата е пат ако ниту едно теме не се повторува два или повеќе пати во низата x0, u1, x1, u2, … , un, xn. Маршрутата е циклус ако е затворена верига. Маршрутата е контура (циклус) ако е затворена и ниедно теме не се повторува два или повеќе пати во низата x0, u1, x1, u2, … , un, xn, освен што x0=xn.
За графот G=(X,U) велиме дека е бипартитен (дводелен) ако множеството темиња може да се разбие на две непразни дисјунктни подмножества X1 и X2, така што за секое ребро (x,y) од G да важи x припаѓа на X1, y да припаѓа на X2.
За едно подмножество темиња S од графот G=(X,U) велиме дека е внатрешно стабилно ако пресекот на U(S) и S е празно можество, при што U(S) е унија од сите множества U(x) (x\in S), a U(x)={y|y\in X & (x,y)\in U}. Со други зборови, ниту еден пар различни темиња од S не се меѓусебно соседни во G. Со Ф ја означуваме фамилијата од сите внатрешно стабилни подмножества темиња на графот G=(X,U). Број на внатрешна стабилност на графот G е бројот а(G)=max|S|, S \in Ф.
Правилно обојување на граф е придружување бои на темињата на графот, при што ниеден пар соседни темиња не добиваат иста боја. Графот се нарекува n-обојлив ако неговите темиња може да се обојат со n бои. Хроматски број h(G) на графот G=(X,U) е најмалиот број бои со кои графот може правилно да се обои.
Теорема 2. За бројот на внатрешна стабилност a(G) и хроматскиот број k(G) на графот G со p темиња важи a(G)h(G) >= p.
Теорема 3. (Теорема на König) Графот е бихроматски (има хроматски број 2) ако и само ако е бипартитен.
Условот графот да биде бипартитен е еквивалентен со тоа G да не содржи контури со непарна должина.
Последица. Хроматскиот број на еден граф G е поголем или еднаков на 3 ако и само ако G има непарен циклус.
Теорема 4. За секој сврзан граф G важи дека h(G) е помал или еднаков на d(G)+1.
Теорема 5. (Теорема на Brooks) За хроматскиот број на сврзаниот граф G кој не е комплетен и кој не е непарен циклус важи h(G) <= d(G).
Во следниот пример, теоремата на Brooks е употребена за полесно наоѓање на хроматскиот број на графот чиј темиња се општините на градот Скопје, а рабови се отсечките кои поврзуваат темиња на две соседни општини.
Графот G кој е добиен на овој начин има 10 темиња и 16 рабови.
|
Степените на темињата се следните:
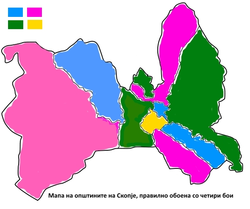
deg(ЃП)=2, deg(К)=6, deg(КВ)=3, deg(А)=3, deg(Ц)=5, deg(ШО)=1, deg(Б)=4, deg(Ч)=4, deg(ГБ)=4, deg(С)=2. Овој граф не е ниту комплетен, ниту регуларен. Од последицата на теоремата 3 имаме дека за хроматскиот број h(G) на графот G важи: 3 <= h(G). Графот G не претставува циклус со непарна должина. Темето K има најголем степен, кој е еднаков на 6. Од теоремата на Брукс, добиваме дека важи h(G) <= 6, т.е. h(G) \in {3,4,5}. Со непосредна проверка, тргнувајќи од најмалата можна вредност, добиваме дека h(G)=4. Според тоа, мапата на Скопје можеме правилно да ја обоиме со четири бои. |
Литература
[1] Д. Цветковиќ, Р. Шокаровски, Основи на теоријата на графови, Библиотека „математичка школа“, Скопје 1975
[2] Г. Рингељ, Теорема о раскраске карт, Издатељство „Мир“, Москва, 1977
[1] Д. Цветковиќ, Р. Шокаровски, Основи на теоријата на графови, Библиотека „математичка школа“, Скопје 1975
[2] Г. Рингељ, Теорема о раскраске карт, Издатељство „Мир“, Москва, 1977
Автор:
Гордана Николовска, студент на Институт за математика, Природно математички факултет, Скопје
Награден труд (прво место) на 43. Приматијада одржана од 28.04.2015 до 01.05.2015, Албена, Р. Бугарија.
Ментор: проф. д-р Весна Целакоска-Јорданова
Објавено на ПОИМ:
9 мај 2016
Начин на цитирање на статијата:
Г. Николовска, Боење графови, Портал ПОИМ на Институтот за математика, ПМФ, Скопје, 9 мај 2016, http://poim-pmf.weebly.com/boenje-grafovi.html
Download (PDF)
Авторизираните статии објавени на Порталот подлежат на законска заштита. Се забранува користење на статиите без наведување на авторот или изворот.
Гордана Николовска, студент на Институт за математика, Природно математички факултет, Скопје
Награден труд (прво место) на 43. Приматијада одржана од 28.04.2015 до 01.05.2015, Албена, Р. Бугарија.
Ментор: проф. д-р Весна Целакоска-Јорданова
Објавено на ПОИМ:
9 мај 2016
Начин на цитирање на статијата:
Г. Николовска, Боење графови, Портал ПОИМ на Институтот за математика, ПМФ, Скопје, 9 мај 2016, http://poim-pmf.weebly.com/boenje-grafovi.html
Download (PDF)
Авторизираните статии објавени на Порталот подлежат на законска заштита. Се забранува користење на статиите без наведување на авторот или изворот.