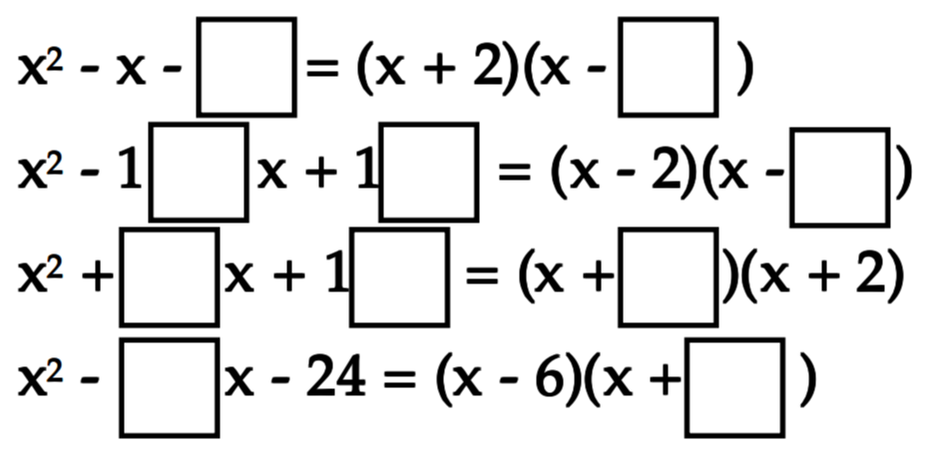Како резултат од одржаните семинари „Математика и примени“, Институтот за математика публикуваше неколку зборници од научно-популарни трудови и зборници на трудови за наставата по математика во рамки на научно-популарната едиција Математички омнибус. Во овие трудови, излагачите на досегашните Семинари се потрудија да ни ја пренесат пораката за убавината и корисноста на математиката и дека таа е јазик на нашата реалност.
2 / 2
|
Споредбена анализа на класичната настава и наставата преку системи за далечинско образование во услови на корона-криза, за некои математички универзитетски курсеви (PDF)
13 април 2022 во МАТЕМАТИЧКИ ОМНИБУС (НАСТАВА) Наставата на повеќето математички предмети на ФИНКИ се состои од предавања, аудиториумски и лабораториски вежби. Класичниот начин на предавања и аудиториумски вежби се одвиваше во училница, со користење на табла и видео-бим. Новонастанатата состојба во државава и многу пошироко – на целата планета, причинета од кризата на вирусот кој ја предизвикува болеста COVID-19, диктираше потреба од прилагодување на наставата и испитите на голем дел од универзитетските курсеви. Започнувајќи од 17.3.2020 год., па сѐ до март 2021 год., изведувањето на наставата и испитите е комплетно преку системи за далечинско учење. Тоа е реализирано со користење на видео конференцискиот систем BigBlueButton (BBB), имплементиран во студентскиот сервис Courses, односно на официјалните интернет страници на ФИНКИ на платформата за е-учење Moodle. Направена е споредба на изведувањето на наставата и резултатите од испитите од неколку математички курсеви. Труд објавен во Математички омнибус 10 (2021). |
|
Open Middle проблеми во наставата по математика во основното и средното образование (PDF)
8 април 2022 во МАТЕМАТИЧКИ ОМНИБУС (НАСТАВА) Со традиционалните проблеми, на учениците им се кажуваат чекорите што треба да ги направат за да го решат проблемот. Лесната структура и недостатокот на можности на традиционалните проблеми ја ограничуваат флексибилноста и креативноста и го ослабуваат жарот за учење кај најголем број ученици. Учениците прават проверки или се откажуваат, се чувствуваат фрустрирани или само ги следат чекорите кои се запишани во нивните тетратки (белешки) наместо да размислуваат и да прават рефлексија на нивните стратегии. Наспроти традиционалните проблеми, Open Middle проблемите многу често побаруваат од ученците да пронајдат стратегија според која ќе го одберат видот на својот одговор, како на пример, најмалото или најголемото решение или, пак, она решение кое е најблиско до некој однапред зададен број. Ваквата структура на овие проблеми побарува од учениците прво да се убедат себеси, а потоа да ги убедат и другите дека нивното решение е најдоброто можно. Со помош на овие проблеми кај ученците се поттикнува дискусијата за проблемите и продолжуваат со размислувањето и по добивањето на првобитното решение (одговор). Кај нив се развива навика за повеќекратни обиди за решавање на проблемот. Притоа, секој нареден пат си поставуваат пред себе цел да бидат подобри од претходниот обид или да добијат подобро решение од претходното. Труд објавен во Математички омнибус 10 (2021). |
|
Интеграција во наставните програми (PDF)
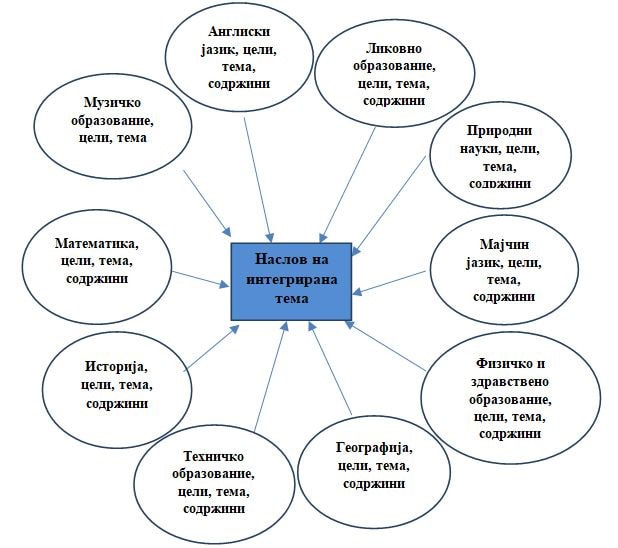
7 февруари 2022 во МАТЕМАТИЧКИ ОМНИБУС (НАСТАВА) Интеграција значи да се координираат, мешаат или здружат одделни делови во функционална, унифицирана и хармонична целина. Интеграцијата им помага на учениците да ги идентификуваат врските, не само помеѓу идеите и процесите во рамките на еден предмет, туку и врските меѓу идеите и процесите во одделни предмети и во светот надвор од училиштето. При интеграција во текот на наставниот процес корист имаат учениците и наставниците. Учениците стекнуваат подлабоки знаења, пројавуваат зголемена активност и интерес, добиваат можност за избирање теми за поучување и развивање вештини за решавање проблеми. Наставниците имаат можност за тимска работа, споделување искуства од работата, запознавање со други содржини, извори и материјали, почитување на интересите и барањата на учениците, a сето тоа ја подобрува атмосферата во училницата. Труд објавен во Математички омнибус 10 (2021). |
|
Методологија за креирање електронски прашања со автоматско оценување (PDF)
5 февруари 2022 во МАТЕМАТИЧКИ ОМНИБУС (НАСТАВА) Учењето преку интернет преку ноќ стана единствен начин на едуцирање и голем број од едукаторите ги затекна целосно неспремни за справување со предизвиците коишто произлегуваат од овој начин на изведување на наставата. Еден од тие предизвици е реалното и објективното оценување на учениците. За среќа, методи, техники и алатки за електронско и автоматско тестирање се развиваат повеќе од 20 години, па технологијата веќе беше развиена на ниво да одговори на повеќето од предизвиците од овој домен. Секако, тоа само за себе не е доволно ако наставниците не знаат да ги користат тие алатки. Ќе се задржиме на можностите што ги нуди платформата Мoodle од повеќе аспекти: видови прашања, постапка за креирање прашања, стратегија за креирање и оценување на прашањата, односно доделување поени, како и стратегија за креирање на тестот во целост. Труд објавен во Математички омнибус 10 (2021). |
|
Примена на комплексните броеви во наставата по физика (PDF)
23 јануари 2022 во МАТЕМАТИЧКИ ОМНИБУС (НАСТАВА) Корелацијата помеѓу наставните содржини по математика и физика отсекогаш претставувала една од клучните алки за ефикасна настава по физика. Во трудот се прикажани наставни единици од физиката во кои може да се користат свoјствата на комплексните броеви како на пример нивното геометриско претставување, разните облици на запишување и модул на комплексeн број. Денес комплексните броеви имаат примена во теоријата на управување, електромагнетизмот, сигналната анализа, динамиката на флуиди, квантната механика и во други области. Колку е нивната примена важна во учењето на еден инженер по физика или професор по физика, на студентите по физика од прва година на Универзитетот „Ројал Холовеј“ во Лондон почетокот на учебната година ја започнува со химна, посветена на комплексните броеви. Труд објавен во Математички омнибус 10 (2021). |
|
Можности за примена на современата технологија во наставата по математика (PDF)
16 јануари 2022 во МАТЕМАТИЧКИ ОМНИБУС (НАСТАВА) Денес, во време на најразлична современа технологија, процесот на изведување на наставата по математика мора да се менува и да се прилагодува на барањата од современото општество. Наставната технологија станува сѐ помодерна и поинспиративна и за наставниците и за учениците. Со користењето на новите технологии, наставните содржини на учениците може да им бидат достапни секогаш и секаде, во различни форми, овозможувајќи им на тој начин непречена и константна соработка со наставниците и меѓусебно. Главна цел на примената на овие образовни технологии во наставата е зголемување на степенот на интерактивност. Императив за наставниците, но и за родителите е примената на што поголем број технологии во наставниот план и програма, бидејќи на тој начин тие стануваат поквалитетни, се зголемува персонализацијата на процесот на учење, односно се прилагодува на потребите на секој ученик индивидуално. Труд објавен во Математички омнибус 10 (2021). |
|
Критичко размислување, ефективна комуникација и решавање проблеми (PDF)
16 јануари 2022 во МАТЕМАТИЧКИ ОМНИБУС (НАСТАВА) Проблемите со кои се соочуваме денес се импликација на начинот на којшто размислувавме додека ги решававме проблемите од вчера. Впечатокот дека се соочуваме со сѐ посложени проблеми, укажува на потребата посериозно да размислуваме за тоа како размислуваме. Во овој труд е предочена причинско-последична поврзаност на две клучни компетенции: способност за решавање проблеми и критичко размислување, низ призма на „видливост“ на мислите, проблемите и решенијата, наречена ефективна комуникација. Труд објавен во Математички омнибус 10 (2021). |
|
Улогата, примената и важноста на туторството во образованието на 21 век (PDF)
3 декември 2021 во МАТЕМАТИЧКИ ОМНИБУС (НАСТАВА) Ќе зборуваме за туторството во рамките на формалното образование, коешто е присутно од предучилишната возраст до високото образование. Иако скоро секој образован возрасен човек може да му помогне на ученик од пониските одделенија на основното образование во вежбање читање и говор, броење или основна математика, со голема доза на стрпливост при објаснувањето, сепак, постојат области каде што се потребни посебни стручни познавања, искуство и континуирана надградба на туторот за ефективна работа. Активностите во воспитно-образовниот процес, треба да бидат такви што пред сѐ ќе ги создадат потребните предуслови ученикот да се развие во отворена, самостојна, креативна и карактерна личност, во согласност со неговите развојни потреби и интереси, a училиштето да стане место за социјализација на учениците и привлечна средина за учење. Во дидактичкo-методските техники за оваа намена, на високо позиционирано место сигурно ќе се најде соученичкото туторство, од кое резултатите се повеќе од очигледни. Труд објавен во Математички омнибус 10 (2021). |
|
Египетски дропки (PDF)
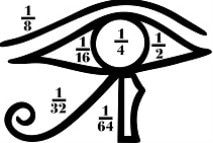
4 ноември 2021 во МАТЕМАТИЧКИ ОМНИБУС (НАСТАВА) Сте се запрашале ли како Египќаните ги запишувале броевите? А, како пак ги запишувале дропките? Од друга страна, навидум две далечни прашања: дали збирот на две различни дропки со броител 1 и именител позитивен цел број, (кои ќе ги нарекуваме единични дропки) е секогаш единична дропка? Дали е можно секоја единична дропка да ја претставиме во вид на збир од две единични дропки? Каква е врската помеѓу првиот пар прашања и вториот пар прашања? Нашите сознанија за египетската математика се должат во голема мера на два египетски папируса. Едниот е Рајндовиот папирус, а вториот е Moсковскиот папирус. Ќе се осврнеме на Рајндовиот папирус, на алгоритмот на Фибоначи, на бесконечни претставувања и на примената во наставата. Труд објавен во Математички омнибус 10 (2021). |