|
МАТЕМАТИЧКИ ОМНИБУС
|
|
Како резултат од одржаните семинари „Математика и примени“, Институтот за математика публикуваше неколку зборници од научно-популарни трудови и зборници на трудови за наставата по математика во рамки на научно-популарната едиција Математички омнибус. Во овие трудови, излагачите на досегашните Семинари се потрудија да ни ја пренесат пораката за убавината и корисноста на математиката и дека таа е јазик на нашата реалност.
2 / 2
|
Експоненцијални фамилии на распределби на веројатност (PDF)
20 ноември 2024 во НАУЧНО-ПОПУЛАРНИ СТАТИИ Во теоријата на веројатност и статистика, под експоненцијална фамилија се подразбира параметарско множество на распределби на веројатност кои имаат одредено својство. Тие распределби се генерализација на неколку основни веројатносни модели со заеднички специјални особини. Терминот "експоненцијални фамилии" е релативно нов. До средината на 1950-тите години оваа класа на распределби на веројатност била позната како "Купман–Дармоа–Питман" фами–лии на распределби на веројатност (во чест на тројцата истакнати статистичари кои работеле посебно, во три различни земји). Труд објавен во Математички омнибус 11 (2024) |
|
Филозофските песни свирени од математичката труба на Aрхангел Гаврил (PDF)
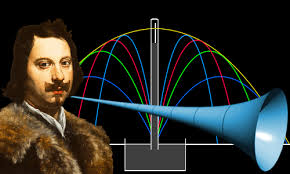
30 декември 2023 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Еден од интересните математички парадокси е парадоксот именуван како „Трубата на Архангел Гаврил“, откриен од италијанскиот математичар од XVII-ти век Евангелиста Торичели. Самото име на парадоксот доаѓа од проблемот на спојот на конечното и бесконечното, иманентното и трансцендентното, односно световното и божественото, спор што во Средниот век се расправал нашироко низ целата академска јавност, а пак Архангелот Гаврил е еден од седумте архангели, кои седат на престолот Божји, и го најавува Судниот ден со дување во труба. Таа досетливост го прави овој парадокс уште попривлечен за разгледување. Трубата на Гаврил, дефинирана од Торичели, всушност претставува геометриско тело со бесконечна површина и конечен волумен. Во овој труд ќе се претстави историскиот пат до „Трубата на Архангел Гаврил“, што се случувало на филозофски план во периодот кога е поставен овој парадокс, ќе се претстави самиот математички парадокс без да се навлегува во стручно-математичките начини на сметање и решавање на парадоксот... Труд објавен во Математички омнибус 11 (2024) |
|
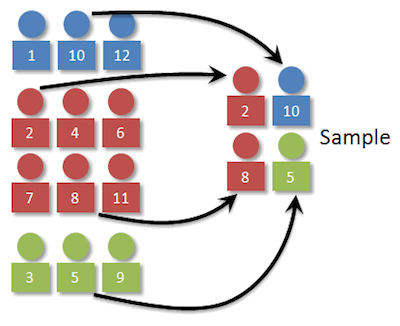
Стратифициран случаен примерок (PDF)
1 декември 2023 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Стратифициран случаен примерок е примерок кој се користи за истражувања во кои популацијата е хетерогена, односно секој елемент на популацијата не ги задоволува сите каракте– ристики кои се предмет на истражување. Всушност елементите на популацијата се разликуваат еден од друг по одредена карактеристика. Поради тоа, се формираат подгрупи од популацијата кои се хомогени, односно сите елементи на подгрупата задово– луваат исти карактеристики. Да забележиме дека, карактерис– тиките според кои се формирани подгрупите од популацијата се дел од карактеристиките кои се предмет на истражување. Вака формираните подгрупи ги нарекуваме стратуми. Формирањето на овие стратуми може да се изведе со помош на техники за избор на кластер примерок или со техники за избор на стратифициран примерок, во зависност од природата на истражувањето. Труд објавен во Математички омнибус 11 (2024) |
|
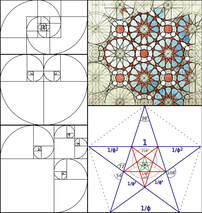
Нераскинливата врска меѓу математиката, природата и уметноста (PDF)
29 ноември 2023 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Пропорцијата на златниот пресек претставува извор на совршена убавина – онаа за која вечно трагале уметниците. Цајзинг е човекот што е најзаслужен златниот пресек да не се набљудува само како математички и геометриски феномен, туку како израз на убавина и комплетност и во природата и во уметноста. Негова е теоријата дека дека целиот универзум е изграден во склад со таа пропорција. Во трудот покажавме дека златниот пресек и Фибоначиевите броеви се присутни насекаде, во: математиката, анатомијата на човечкото тело, природата, архитектурата, сликарството, вајарството, музиката, литературата, па дури и во вселената. Златниот пресек и Фибоначиевите броеви се манифестираат во бројни форми, на разни начини, на повеќе нивоа и во различни концепти, или кратко кажано, нивната појавност има широк спектар на варијации. Труд објавен во Математички омнибус 11 (2024) |
|
Задача на најдобар избор и оптимално запирање (PDF)
16 август 2022 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) При барањето соодветен кандидат за работното место, најдобро паркинг место, идеален стан за живеење, па дури и животен партнер од соништата, се соочуваме со последователно носење одлуки. Во секој чекор треба да одлучиме дали да ја запреме потрагата и да го направиме изборот или да ризикуваме да продолжиме со барањето во надеж дека ќе направиме подобар избор. Математичкиот пристап кој го решава овој вид проблеми е познат како оптимално запирање. Проблемите на оптимално запирање се среќаваат и во статистиката при тестирање хипотези и оценување параметри, во операционите истражувања при замена на машина, нарачка на стоки, во економијата при потрага на високо платени работни места или намирници со ниски цени, на финансиските пазари при тргувањето со акции, итн. Во овој труд го илустрираме оптималното запирање на познати примери од таа област и даваме преглед на некои резултати од теоријата на оптимално запирање. Труд објавен во Математички омнибус 9 (2021). |
|
Нетранзитивни коцки (PDF)
11 март 2022 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Нетранзитивните коцки се фасцинантна тема во применетата веројатност. Тие за прв пат доаѓаат во центарот на вниманието како резултат на трудот на Мартин Гарднер и претставуваат еден проблем од поголемата класа на нетранзитивни „парадокси“, кои го вклучуваат и добро познатиот Кондорсов парадокс на гласање. Се разгледуваат неколку примери за нетранзитивни коцки: коцки со броевите од 1 до 18, коцки на Шајнхаус-Трибула и коцките на Ефрон. Труд објавен во Математички омнибус 9 (2021). |
|
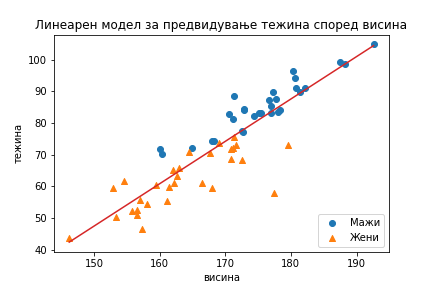
Логистичка регресија и нејзина примена на задачи од бинарна класификација (PDF)
22 февруари 2022 година во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Статистиката како дел од математиката (или како независна наука) меѓу другото се занимава и со опишување на зависностите помеѓу променливите кои ги разгледува. Променливите главно спаѓаат во една од две категории: независни, врз кои директно имаме влијание, и зависни на чиишто вредности не можеме директно да влијаеме; нивната вредност се менува исклучиво на основа на вредностите на независните променливи. Во контекст на барањата и очекувањата, оваа зависност може да се опише на повеќе начини. Два од нив се: опишувањето на степенот (јачината, моќта) на зависност и конструкција на модел со кој директно би можеле да извршиме предвидување на вредностите на зависната променлива врз основа на вредности на независните променливи. Овој пристап на анализа на зависностите помеѓу променливите главно спаѓа во областа на статистиката наречена регресиона анализа. Труд објавен во Математички омнибус 9 (2021). |
|
Периодичноста кај дискретните динамички системи и теоремата на Шарковски (PDF)
4 декември 2021 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Динамички систем е концепт спротивен на статички систем, со којшто се опишува развојот на одреден математички систем низ времето, кој најчесто се однесува непредвидливо и невообичаено, па од главен интерес е да се изнајде некој ред и правила коишто се кријат во тој хаос. Времето во кое системот се развива може да биде непрекинато или дискретно. Кога времето се мери во дискретни единици, тогаш станува збор за дискретен динамички систем. Теоријата на динамичките системи наоѓа примена во многу области како што се: популационата динамика, биологијата, хемиската кинетика, епидемиологијата, нелинеарната оптика, механиката, невронските мрежи, економијата, електрониката, медицинската дијагностика итн. Во овој труд, кој своевидно е и прво изложување на Теоремата на Шарковски на македонски јазик, целосно е разработен овој познат резултат кој се однесува на класата дискретни системи добиени со итерации на непрекинато пресликување на конкретен интервал, со кој Шарковски успеал да ја објасни нивната периодичност. Труд објавен во Математички омнибус 9 (2021). |
