СТАТИИ ОД МЕСЕЦОТ НА НАУКАТАСе залагаме за зголемување на свеста за местото и улогата на математиката во науките, технологијата, наставата, природата и културата.
|
Златен пресек
Пропорција е однос меѓу две величини. Таа е скриена, но секогаш присутна во композицијата на секое ликовно дело и е еден од одличните чинители на неговата хармонија. Едно од најстарите правила на складноста е пропорцијата наречена златен пресек. Значи, златен пресек е поделба на една отсечка на два дела на тој начин што целата должина спрема големиот дел се однесува исто како поголемиот дел спрема помалиот.
Важноста на пропорцијата во уметноста детално ја опишал грчкиот уметник Поликлет кој сметал дека тајната на уметноста е во складниот однос на величината на пропорцијата. Затоа кога ќе ја погледнеме античката архитектура ние несвесно гледаме нешто што ни е слично нам и затоа тоа ни се допаѓа.
Важноста на пропорцијата во уметноста детално ја опишал грчкиот уметник Поликлет кој сметал дека тајната на уметноста е во складниот однос на величината на пропорцијата. Затоа кога ќе ја погледнеме античката архитектура ние несвесно гледаме нешто што ни е слично нам и затоа тоа ни се допаѓа.
НЕКОЛКУ КОНСТРУКТИВНИ ЗАДАЧИ ВО ВРСКА СО ЗЛАТЕН ПРЕСЕК
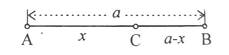
Дадена отсечка AB чија должина е а (Црт.1), треба да се подели со точка C на два дела така што должината на отсечката AB спрема поголемиот дел AC, чија должина е x, се однесува како нејзиниот поголем дел AC спрема помалиот дел CB (чија должина е a - x), т.е. a : x = x : (a-x).
Ваквата поделба на отсечката AB се нарекува поделба по златен пресек.

Да ја изведеме оваа конструкција.
1. Цртаме отсечка AB.
2. Во точката B повлекуваме нормала.
3. На неа избираме точка Е таква што должината на отсечата ВЕ да биде 1/2 од должината на отсечката АВ.
4. На отсечката EA избираме точка D таква што должината на отсечката ЕD да биде еднаква на должината на отсечката BE.
5. На отсечката АB избираме точка C таква што должината на отсечката AC да биде еднаква на должината на отсечката AD.
6. Тогаш AC : CB = AB: AC, т.е. важи a : b = (a+b) : a
(при што должината на отсечката AC e a, a должината на отсечката CB е b).
7. Значи точката C претствува златен пресек на отсечката AB.
1. Цртаме отсечка AB.
2. Во точката B повлекуваме нормала.
3. На неа избираме точка Е таква што должината на отсечата ВЕ да биде 1/2 од должината на отсечката АВ.
4. На отсечката EA избираме точка D таква што должината на отсечката ЕD да биде еднаква на должината на отсечката BE.
5. На отсечката АB избираме точка C таква што должината на отсечката AC да биде еднаква на должината на отсечката AD.
6. Тогаш AC : CB = AB: AC, т.е. важи a : b = (a+b) : a
(при што должината на отсечката AC e a, a должината на отсечката CB е b).
7. Значи точката C претствува златен пресек на отсечката AB.
Подолу е дадена една конструкција на златен правоаголник.
|
Конструкцијата ќе ја изведеме на следниот начин.
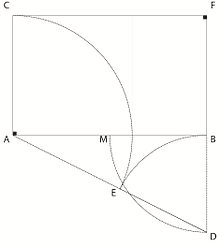
Дадено е: отсечка АВ. Конструкција: 1. Најди ја средината на отсечката АВ (со помош на симетрала на отсечка) и означи ја со М. 2. Повлечи нормала во точката B (како на Црт 2.) 3. Повлечи лак со центар во В и радиус ВМ. 4. Пресечната точка на лакот со нормалата во В означи ја со D. 5. Повлечи ја отсечката AD. 6. Повлечи лак со центар во D и радиус DB, a пресечната точка со отсечката АD означи ја со E (DB = DE). 7. Повлечи права во A нормална на AB. 8. Повлечи лак (или нацртај кружница) со центар во A и радиус АE, а пресечната точка на тој лак со нормалата во А означи ја со C. 9. Потоа нацртај правоаголник со темиња C, A, B, F. |
Ќе дадеме и една конструкција на правилен петаголник. Оваа елегантна конструкција потекнува од 19 век од Јапонија и ја дал Јосифуса Хирано (Yosifusa Hirano).
Конструкција:
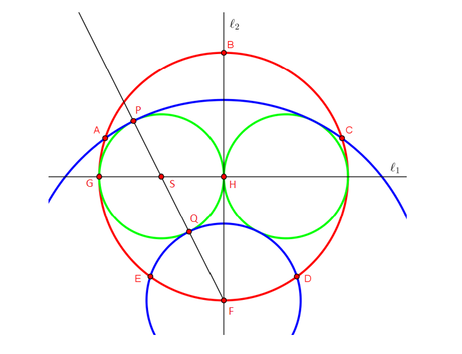
1. Нацртај кружница (на Црт. 3 означена со црвено), со центар во точката H.
2. Повлечи две заемно нормални прави низ H (на Црт. 3 се означени со ℓ1 and ℓ2).
3. Озачи ги пресечните точки со B, F и G.
4. Најди ја средната точка на тсечката GH (повлечи ја симетралата на таа отсечка). Означи ја со S.
5. Нацртај кружница со центар во S и радиус SH (левата зелена кружница).
6. Нацртај уште една (зелена) кружница на десната страна од точката H (следејќи ги чекорите 4 и 5).
7. Повлечи полуправа со почетна точка F, којашто минува низ точката S.
8. Означи ги со P и Q пресечните точки на полуправата со зелената кружница од чекорот 5..
9. Повлечи лаци (со сино) и двата со центар во F и: првиот со радиус FP, а вториот со радиус FQ.
10. Означи ги пресечните точки со A, C, D и E.
11. Повлечи ги отсечките АВ, ВС, CD, DE и EA.
1. Нацртај кружница (на Црт. 3 означена со црвено), со центар во точката H.
2. Повлечи две заемно нормални прави низ H (на Црт. 3 се означени со ℓ1 and ℓ2).
3. Озачи ги пресечните точки со B, F и G.
4. Најди ја средната точка на тсечката GH (повлечи ја симетралата на таа отсечка). Означи ја со S.
5. Нацртај кружница со центар во S и радиус SH (левата зелена кружница).
6. Нацртај уште една (зелена) кружница на десната страна од точката H (следејќи ги чекорите 4 и 5).
7. Повлечи полуправа со почетна точка F, којашто минува низ точката S.
8. Означи ги со P и Q пресечните точки на полуправата со зелената кружница од чекорот 5..
9. Повлечи лаци (со сино) и двата со центар во F и: првиот со радиус FP, а вториот со радиус FQ.
10. Означи ги пресечните точки со A, C, D и E.
11. Повлечи ги отсечките АВ, ВС, CD, DE и EA.
ЗЛАТНИОТ ПРЕСЕК ВО АРХИТЕКТУРАТА И ВО УМЕТНОСТА
Во текот на вековите, истражувани се најдобрите пропорциски односи за градбите, а притоа ниту еден дел од градбата да не се измени. Во архитектонските композиции се истражувани ефекти како контраст помеѓу полното (ѕидот) и празното (столбовите пред ѕидот), а за постигнување на хармонија истражувана е рамнотежа меѓу столбот и тежината која паѓа врз него. Целата античка архитектура се темели врз овие композицискиот принцип засниван на должината на долниот радиус на столбот како релативна мерка за пропорција. Архитектонскиот израз на грчкиот храм е сведен на достоинственост, убавина или раскош, на кои одговараат дорскиот, јонскиот и коринтскиот стил.
За разлика од грчката архитектура, египетската и месопотамската архитектура се монументални. Во споредба со нив грчката архитектура е со помали димензии. Имено, кај грчката архитектура по правило монументалноста на објектите не е гледана во големината туку во начинот на одредување на рамнотежа помеѓу главните архитектонски елементи, во ритамот на вертикалите, во пропорциските односи и во складноста.
За разлика од грчката архитектура, египетската и месопотамската архитектура се монументални. Во споредба со нив грчката архитектура е со помали димензии. Имено, кај грчката архитектура по правило монументалноста на објектите не е гледана во големината туку во начинот на одредување на рамнотежа помеѓу главните архитектонски елементи, во ритамот на вертикалите, во пропорциските односи и во складноста.
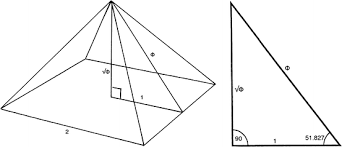
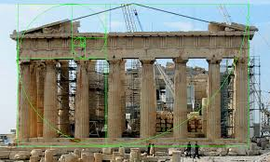
Овие архитекти сметале дека градбите имаат исклучителен изглед ако димензиите им се одредувани по златен пресек. Се верувало и дека ако се изградени по принципот на златен пресек ќе имаат магични моќи. Златниот пресек се сметал за совршена пропорција или божествена пропорција. Познати објекти кои се градени по овој принцип се: египетските пирамиди, Партенон во Атина - дело на познатите архитекти Ихтинос и Каликратес и склупторот Фидиј , склуптури во Акропол (дело на Фидиј), Таџ Махал во Индија, црквата Нотр Дам во Париз, Ајфеловата кула во Париз и многу други.
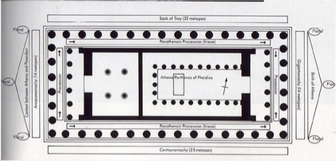
Малку подетално ќе се задржиме на Партенон на атинскиот Акропол, изграден 447 - 434 г.од п.н.е. Неговиот модул изнесува 95 cm, висината на подножјето на столбот е 160 cm, столбот е 1031 cm, димензијата на гредата е 330 cm и триаголниот кров е 450 cm. Вкупната висина на објектот е 1971 cm. Партенон е еден од најголемите антички храмови кој е изграден во совршен пропорции, што може да се види и од пропорциите на неговата основа (види го цртежот долу десно).
Секако, еден од најубавите и воедно најмонументални градби во поновата историја е Таџ Махал (слика долу лево). Таџ Махал е изграден помеѓу 1631 - 1654 год. Требало да претставува најголема и најубава гробница во целиот свет. Неговата висина изнесува 75 m, а димензиите на целиот комплекс се 300 m на 560 m. Целата градба е изработена од бел мермер.
На цртежот е дадена и Ајфеловата кула, при што се означени пропорциите кои се во златен пресек.
Во претходните разгледувања рековме дека пропорцијата на златен пресек, која уште се нарекува божествена пропорција се јавува и во уметноста. Така, на пример, познатото ремек дело Мона Лиза на Леонардо да Винчи (слика долу лево) во основата на својата конструкција го има златниот триаголник и златната спирала.
Друг карактеристичен пример од уметноста е кипот на Аполон, кој се смета за симбол на убавина на машкото тело, а чии пропорции се поврзани со златниот пресек. Вакви и слични примери можат да се видат и во делата на многу други уметници.
Користена литература:
[1] А. Иванова, Д. Велинов, Златен пресек, омилена пропорција на архитекстите, Нумерус XLI-3 (2015/2016), стр.1-5.
[2] Phi, the Golden Ratio and Geometry, https://www.goldennumber.net/geometry
[3] Descriptive Geometry/Mathematical constructions/Golden Ratio, https://en.wikibooks.org/wiki/Descriptive_Geometry/Mathematical_Constructions/Golden_Ratio
[4] P. Desai, Construction of Fibonacci Spiral and Geometry in Golden Hexagon using Golden Sections, Interwoven: An Interdisciplinary Journal of Navrachana University, Vol. 1, Issue 1, June 2017, https://nuv.ac.in/wp-content/uploads/2018/10/3_Math_01_March_2017.pdf
[5] В. Целакоска-Јорданова, Неколку задачи за златен пресек, Сигма 59, Vol. 24, бр. 3, 2002/2003, 42-45
Автор:
Јована Бранкова, IX одд., ООУ „Никола Карев“, Пробиштип
Проект презентиран на Ноември – Месец на науката 2019 во категоријата 7-9 одд.
Професор:
Живко Ангеловски
Избор и обработка:
проф. д-р Весна Целакоска-Јорданова
Објавено на ПОИМ:
20 април 2020 година
Начин на цитирање на статијата:
Ј. Бранкова, Златен пресек, Портал ПОИМ на Институтот за математика, ПМФ, Скопје, 20 април 2020 год., http://poim-pmf.weebly.com/zlaten-presek.html
[1] А. Иванова, Д. Велинов, Златен пресек, омилена пропорција на архитекстите, Нумерус XLI-3 (2015/2016), стр.1-5.
[2] Phi, the Golden Ratio and Geometry, https://www.goldennumber.net/geometry
[3] Descriptive Geometry/Mathematical constructions/Golden Ratio, https://en.wikibooks.org/wiki/Descriptive_Geometry/Mathematical_Constructions/Golden_Ratio
[4] P. Desai, Construction of Fibonacci Spiral and Geometry in Golden Hexagon using Golden Sections, Interwoven: An Interdisciplinary Journal of Navrachana University, Vol. 1, Issue 1, June 2017, https://nuv.ac.in/wp-content/uploads/2018/10/3_Math_01_March_2017.pdf
[5] В. Целакоска-Јорданова, Неколку задачи за златен пресек, Сигма 59, Vol. 24, бр. 3, 2002/2003, 42-45
Автор:
Јована Бранкова, IX одд., ООУ „Никола Карев“, Пробиштип
Проект презентиран на Ноември – Месец на науката 2019 во категоријата 7-9 одд.
Професор:
Живко Ангеловски
Избор и обработка:
проф. д-р Весна Целакоска-Јорданова
Објавено на ПОИМ:
20 април 2020 година
Начин на цитирање на статијата:
Ј. Бранкова, Златен пресек, Портал ПОИМ на Институтот за математика, ПМФ, Скопје, 20 април 2020 год., http://poim-pmf.weebly.com/zlaten-presek.html
Авторизираните статии објавени на Порталот подлежат на законска заштита. Се забранува користење на статиите без наведување на авторот или изворот.