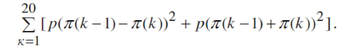НАУЧНО - ПОПУЛАРНИ СТАТИИСе залагаме за зголемување на свеста за местото и улогата на математиката во науките, технологијата, наставата, природата и културата.
|
ЗАДАЧАТА НА ПАТУВАЧКИОТ ТРГОВЕЦ - ЕДНОСТАВНА ФОРМУЛАЦИЈА, ШИРОКА ПРИМЕНА, ТЕШКА ЗА РЕШАВАЊЕ
(Темата е презентирана и на Првиот семинар „Математика и примени“, 14 декември 2016)
(апстракт), (презентација), (ПОИМ статија), (труд)
(апстракт), (презентација), (ПОИМ статија), (труд)

Задачата на патувачкиот трговец (ЗПТ) гласи:
Патувачки трговец треба да помине неколку града, да го посети секој град точно еднаш, да се врати во градот од каде што го започнал патувањето и при тоа трошокот за патување да биде минимален.
ЗПТ е една од најпознатите комбинатрни оптимизациони задачи чија формулација во теоријата на графови е следната: да се одреди минимален циклус (тура) кој минува само еднаш низ секое теме на дадениот граф.
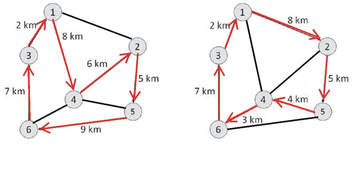
На Слика 1 е даден пример за две тури низ шест града, и нивните прикази со граф, од кои втората тура е минималната тура со вкупна должина на патот од 29 km, во споредба со првата тура со вкупна должина од 37 km.
Патувачки трговец треба да помине неколку града, да го посети секој град точно еднаш, да се врати во градот од каде што го започнал патувањето и при тоа трошокот за патување да биде минимален.
ЗПТ е една од најпознатите комбинатрни оптимизациони задачи чија формулација во теоријата на графови е следната: да се одреди минимален циклус (тура) кој минува само еднаш низ секое теме на дадениот граф.
На Слика 1 е даден пример за две тури низ шест града, и нивните прикази со граф, од кои втората тура е минималната тура со вкупна должина на патот од 29 km, во споредба со првата тура со вкупна должина од 37 km.
Слика 1. Две тури низ шест града, од кои првата е со вкупна должина од 37 km, а втората 29 km.
Чести се формулациите на ЗПТ како задача на целобројно програмирање. Една од првите такви формулации е предложена од Dantzig, Fulkerson и Johnson (DFJ):
каде Xij, i <> j е бинарна променлива која прима вредност 1 ако и само ако патот (i, j) кој ги поврзува градовите i и j е дел од оптималното решение, а Cij е должината на патот (i, j). Во оваа формулација, функцијата на целта (1) е вкупниот трошок на турата, ограничувањата (2) и (3) се ограничувања на степенот кои покажуваат дека во секој град се влегува точно еднаш и се излегува точно еднаш. Ограничувањата (4) се ограничувања за елиминација на поттури со кои се попречува формирање на поттури, односно тури со помалку од n града.
Задачата на патувачкиот трговец (ЗПТ) има едноставна формулација, широка примена, но тешка е за решавање. Најнапред ќе ѕирнеме во историјата, да видиме од каде потекнува оваа задача, а потоа ќе изложиме неколку нејзини примени, а на крајот ќе се осврнеме на тежината на нејзиното решавање.
1. Кратка историја
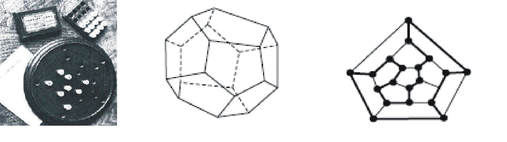
Корените на ЗПТ се смета дека датираат од 1857 година, кога Сер Вилјам Хамилтон, ирски математичар, физичар и астроном (1805 - 1865), ја предложил сложувалката наречена „Икозиска игра“ (Icosian game). Сложувалката се состоела од додекаедар на кој секое од 20-те темиња било именувано според некој главен светски град. Играта била дистрибуирана во вид на табла со дупки, на местото од темињата на графот кој соодветствува на додекаедар, кои ги означувале градовите и боцки кои означувале дали градот е посетен (Слика 2 а). Целта на играта била да се констурира пат по рабовите на додекаедарот (Слика 2 б) кој поминува низ секој град (теме) точно еднаш и се враќа во градот од каде почнал. Со други зборови, требало да се конструира Хамилтонов циклус во граф кој соодветствува на додекаедар (Слика 2 в), т.е. затворен пат кој минува само еднаш низ секое теме од графот. Интересен факт е тоа што Сер Вилјам Хамилтон, во 1959 година, ја продал оваа игра на лондонски произведувач на игри, за само 25 фунти. Подоцна, токму според Сер Вилијам Хамилтон, Хамилтоновите графови (графови кои содржат Хамилтонов циклус) го добиле своето име.
Задачата на патувачкиот трговец (ЗПТ) има едноставна формулација, широка примена, но тешка е за решавање. Најнапред ќе ѕирнеме во историјата, да видиме од каде потекнува оваа задача, а потоа ќе изложиме неколку нејзини примени, а на крајот ќе се осврнеме на тежината на нејзиното решавање.
1. Кратка историја
Корените на ЗПТ се смета дека датираат од 1857 година, кога Сер Вилјам Хамилтон, ирски математичар, физичар и астроном (1805 - 1865), ја предложил сложувалката наречена „Икозиска игра“ (Icosian game). Сложувалката се состоела од додекаедар на кој секое од 20-те темиња било именувано според некој главен светски град. Играта била дистрибуирана во вид на табла со дупки, на местото од темињата на графот кој соодветствува на додекаедар, кои ги означувале градовите и боцки кои означувале дали градот е посетен (Слика 2 а). Целта на играта била да се констурира пат по рабовите на додекаедарот (Слика 2 б) кој поминува низ секој град (теме) точно еднаш и се враќа во градот од каде почнал. Со други зборови, требало да се конструира Хамилтонов циклус во граф кој соодветствува на додекаедар (Слика 2 в), т.е. затворен пат кој минува само еднаш низ секое теме од графот. Интересен факт е тоа што Сер Вилјам Хамилтон, во 1959 година, ја продал оваа игра на лондонски произведувач на игри, за само 25 фунти. Подоцна, токму според Сер Вилијам Хамилтон, Хамилтоновите графови (графови кои содржат Хамилтонов циклус) го добиле своето име.
а) б) в)
Слика 2. а) Слагалицата „Икозиска игра“ од 1857 година, б) Додекаедар со 20 темиња,
в) Граф кој соодветствува на додекаедорот со впишан Хамилтонов циклус.
Слика 2. а) Слагалицата „Икозиска игра“ од 1857 година, б) Додекаедар со 20 темиња,
в) Граф кој соодветствува на додекаедорот со впишан Хамилтонов циклус.
2. Примена
Иако Хамилтоновата сложувалка не бара „минимизирање на трошокот за патување“, сепак таа претставува пример за ЗПТ од причина што за да се помине секое теме на додекаедарот точно еднаш и да се врати патникот во почетното теме, треба да помине низ точно 20 раба. Бидејќи секој раб е со еднаква должина, тоа би значело дека секоја Хамилтонова тура е оптимална, па целта е да се најде една таква тура.
Меѓутоа, примената на ЗПТ е многу поразновидна и поширока. Оваа задача се среќава при оптималното дупчење на дупки на електронските плочи, планирањето на оптимален распоред на процеси на една машина, има примена при дистрибуција на производи, планирање на воени мисии, пренесување на податоци преку интернет, позиционирање на сателити за глобална комуникација, како и во рендгенската кристалографија, па дури и дизајнирање на табла за пикадо и други. Во продолжение ќе се задржиме подетално на неколку примени: производство на елекронски плочи, рендгенска кристалографија и дизајн на табла за пикадо.
При производство на електронски плочи неопходно е дупчење на дупки на плочите за позиционирање на компонентите (Слика 3). Проблемот на дупчење на дупките се состои во одредување на патеката по која за минимално време би биле издупчени сите дупки. При дупчење на дупки со различна големина, проблемот станува посложен, бидејќи во тој случај машината за дупчење треба прво да ги издупчи дупките со една иста големина, потоа главата на машината за дупчење да се врати во кутијата со алатки, да ја смени големината на дупчалката, па да продолжи со дупчење на дупките со друга големина. Во тој случај проблемот може да се разгледува како низа од ЗПТ задачи, по една за секоја големина на дупките, при што „градовите“ се позициите на дупките со иста големина, а „растојанието“ меѓу два града е дадено со времето потребно да се придвижи главата на машината од една позиција во друга. Проблемот на дупчење на дупки спаѓа во проблеми со големи димензии, бидејќи некогаш е потребно да се издупчат 500, 1000, па дури и 2000 дупки на една електронска плоча.
Иако Хамилтоновата сложувалка не бара „минимизирање на трошокот за патување“, сепак таа претставува пример за ЗПТ од причина што за да се помине секое теме на додекаедарот точно еднаш и да се врати патникот во почетното теме, треба да помине низ точно 20 раба. Бидејќи секој раб е со еднаква должина, тоа би значело дека секоја Хамилтонова тура е оптимална, па целта е да се најде една таква тура.
Меѓутоа, примената на ЗПТ е многу поразновидна и поширока. Оваа задача се среќава при оптималното дупчење на дупки на електронските плочи, планирањето на оптимален распоред на процеси на една машина, има примена при дистрибуција на производи, планирање на воени мисии, пренесување на податоци преку интернет, позиционирање на сателити за глобална комуникација, како и во рендгенската кристалографија, па дури и дизајнирање на табла за пикадо и други. Во продолжение ќе се задржиме подетално на неколку примени: производство на елекронски плочи, рендгенска кристалографија и дизајн на табла за пикадо.
При производство на електронски плочи неопходно е дупчење на дупки на плочите за позиционирање на компонентите (Слика 3). Проблемот на дупчење на дупките се состои во одредување на патеката по која за минимално време би биле издупчени сите дупки. При дупчење на дупки со различна големина, проблемот станува посложен, бидејќи во тој случај машината за дупчење треба прво да ги издупчи дупките со една иста големина, потоа главата на машината за дупчење да се врати во кутијата со алатки, да ја смени големината на дупчалката, па да продолжи со дупчење на дупките со друга големина. Во тој случај проблемот може да се разгледува како низа од ЗПТ задачи, по една за секоја големина на дупките, при што „градовите“ се позициите на дупките со иста големина, а „растојанието“ меѓу два града е дадено со времето потребно да се придвижи главата на машината од една позиција во друга. Проблемот на дупчење на дупки спаѓа во проблеми со големи димензии, бидејќи некогаш е потребно да се издупчат 500, 1000, па дури и 2000 дупки на една електронска плоча.
Слика 3. Електронска плоча, предна страна (лево) и задна страна (десно)
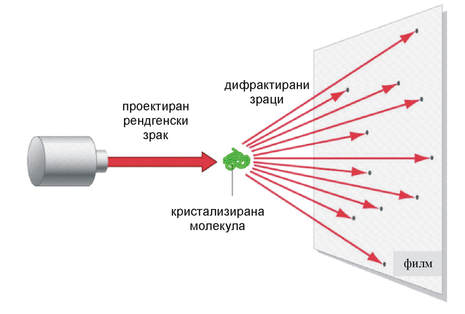
Техниката за одредување на атомската и молекуларната структура на кристалите со дифракција на рендгенски зраци е позната под името рендгенска кристалографија. Оваа постапка подразбира користење на рендгенски дифрактометар кој го мери интензитетот на рефлексија на дифрактираните рендгенски зраци од кристализираната молекула при разни влезни положби на проектираниот рендгенски зрак (Слика 4). Мерењата на интензитетот на рефлексија се одвиваат брзо, но менувањето на положбите за проекција на рендгенски зрак одзема време, ако се има во предвид дека за еден експеримент се потребни околу стотина илјади различни положби. Времето потребно за придвижување од една положба во друга, може прецизно да се пресмета. Тоа што треба да се реши е да се одреди низата положби за чија реализација треба најмалку време, односно треба да се реши ЗПТ со голема димензија.
Слика 4. Дифрактометар
|
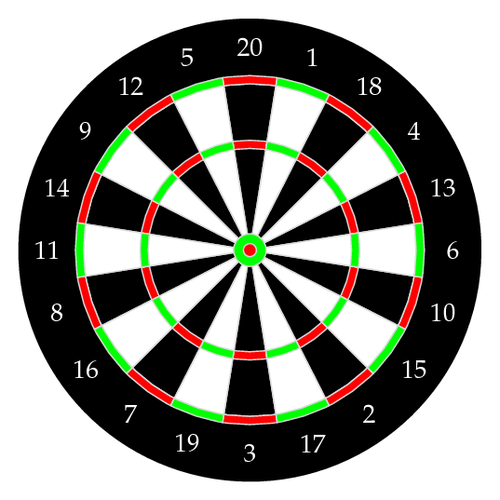
Таблите за пикадо се кружни табли со концентрични кружници и 20 сектори нумерирани со броевите од 1 до 20 (Слика 5). Играчите фрлаат пикада (стрелички) кон секторите и на тој начин освојуваат поени. Најчеста верзија на играта е да се намали почетната вредност 301 до нула со одземање на освоените поени. Затоа, многу поважна е прецизноста да се погоди бројот кон кој играчот цели, отколку воопшто да се погоди број.
Добра игра претставуваа онаа која внесува поголема возбуда како резултат на непредвидливоста. Во овој случај, добар дизајн на една табла за пикадо е оној распоред на броевите од 1 до 20 околу таблата, кој го максимизира ризикот на играчот (ризикот да го погоди бројот кон кој цели). На пример, ако играчот цели кон најголемиот број 20 на таблата за пикадо на Слика 5, има шанси да ги погоди и соседните мали броеви 1 или 5. |
Слика 5. Табла за пикадо
|
За доволно прецизни играчи, разумно е да се претпостави дека секогаш ќе го погодат бројот кон кој целат или ќе погодат негов сосед. Па, нека π=(π(1), π(2), …, π(20)) е пермутација на броевите од 1 до 20. Нека p е веројатноста со која играчот кој цели кон бројот π(k) го погодува бројот π(k±1), при што π(k) треба да се интерпретира како π(k mod 20) за k<1 или k>20. Тогаш, веројатноста да играчот кој цели кон π(k), го погоди π(k) е 1-2p. Еден начин да се максимизира ризикот е да се максимизира очекуваната сума од квадратите на отстапувањата т.е.
Бидејќи p е константа, задачата се сведува на решавање на ЗПТ со должини на патиштата еднакви на Cij=(i - j)².
3. Тешка задача за решавање
Но, дали наоѓањето на оптималната тура е едноставно? Во случај да постои пат меѓу кои било два града, ќе постои и тура низ сите градови. За n града, постојат (n-1)!/2 можни тури (ако ЗПТ е симетрична т.е. Cij=Cji), што претставува навистина голем број на тури за испитување за да се најде минимална тура меѓу сите можни тури. Така за n=15 града постојат 43 589 145 600 можни тури и ако на сметачот му треба една микросекунда за пресметување на една тура, тогаш ќе му требаат околу 12 часа за сите можни тури. Додека за n=100 града, на еден сметач би му требале 10^140 века за наоѓање на оптималното решение, ако ги пресметува сите тури. Затоа, при изборот на алгоритми за решавање на ЗПТ, многу често се прибегнува кон приближните, но ефикасни алгоритми, оние кои наоѓаат приближно оптимално решение за разумно многу време (види [1], [2]).
Горните бројки се доволни за да заклучиме дека решавањето на ЗПТ не е ни малку едноставно. ЗПТ е чест пример во теријата на комплексност на задачите, бидејќи посетата на секоја куќа по должината на најкратката тура е NP задача (што значи дека не постои начин да предвидиме колку долго би ја решавале задачата, без да пробаме да ја решиме), додека проверката дали секоја куќа е посетена е P задача (може да се пресмета најдолгото време за нејзино решавање, времето во најлош случај, без да се решава задачата).
Зборувајќи за комплексноста за решавање на една задача и класите P и NP, неможно е да се заобиколи еден од милениумските проблеми „P vs. NP проблемот“, односно дали класите P и NP се совпаѓаат или не. Интерпретацијата на овој проблем е следната: „Дали задачата која има решение чија точност брзо се проверува, исто така може и брзо да се реши?“, односно „Дали има разлика меѓу решавањето на една задача и сознанието дека сме ја решиле задачата?“. Но, кое е значењето на овој милениумски проблем? Имено, доколку се покаже дека NP не е еднакво на P, тогаш сме „безбедни“, бидејќи некои проблеми се лесни, а некои се тешки за решавање, па сите наши банкарски сметки, интернет картички, лозинки се „безбедни“ затоа што криптоалгоритмите кои ги штитат нашите податоци, се основани на оваа претпоставка. Доколку се покаже дека NP=P, тоа ќе значи дека се' може да се реши исто толку лесно колку и што треба да се провери, или лаички кажано, секој кој знае да вози автомобил, ќе знае и да го направи. Меѓутоа, сознанието дека NP=P би имало практична вредност, само ако доказот на NP=P е конструктивен.
3. Тешка задача за решавање
Но, дали наоѓањето на оптималната тура е едноставно? Во случај да постои пат меѓу кои било два града, ќе постои и тура низ сите градови. За n града, постојат (n-1)!/2 можни тури (ако ЗПТ е симетрична т.е. Cij=Cji), што претставува навистина голем број на тури за испитување за да се најде минимална тура меѓу сите можни тури. Така за n=15 града постојат 43 589 145 600 можни тури и ако на сметачот му треба една микросекунда за пресметување на една тура, тогаш ќе му требаат околу 12 часа за сите можни тури. Додека за n=100 града, на еден сметач би му требале 10^140 века за наоѓање на оптималното решение, ако ги пресметува сите тури. Затоа, при изборот на алгоритми за решавање на ЗПТ, многу често се прибегнува кон приближните, но ефикасни алгоритми, оние кои наоѓаат приближно оптимално решение за разумно многу време (види [1], [2]).
Горните бројки се доволни за да заклучиме дека решавањето на ЗПТ не е ни малку едноставно. ЗПТ е чест пример во теријата на комплексност на задачите, бидејќи посетата на секоја куќа по должината на најкратката тура е NP задача (што значи дека не постои начин да предвидиме колку долго би ја решавале задачата, без да пробаме да ја решиме), додека проверката дали секоја куќа е посетена е P задача (може да се пресмета најдолгото време за нејзино решавање, времето во најлош случај, без да се решава задачата).
Зборувајќи за комплексноста за решавање на една задача и класите P и NP, неможно е да се заобиколи еден од милениумските проблеми „P vs. NP проблемот“, односно дали класите P и NP се совпаѓаат или не. Интерпретацијата на овој проблем е следната: „Дали задачата која има решение чија точност брзо се проверува, исто така може и брзо да се реши?“, односно „Дали има разлика меѓу решавањето на една задача и сознанието дека сме ја решиле задачата?“. Но, кое е значењето на овој милениумски проблем? Имено, доколку се покаже дека NP не е еднакво на P, тогаш сме „безбедни“, бидејќи некои проблеми се лесни, а некои се тешки за решавање, па сите наши банкарски сметки, интернет картички, лозинки се „безбедни“ затоа што криптоалгоритмите кои ги штитат нашите податоци, се основани на оваа претпоставка. Доколку се покаже дека NP=P, тоа ќе значи дека се' може да се реши исто толку лесно колку и што треба да се провери, или лаички кажано, секој кој знае да вози автомобил, ќе знае и да го направи. Меѓутоа, сознанието дека NP=P би имало практична вредност, само ако доказот на NP=P е конструктивен.
Извори:
[1] G. Laporte, The Traveling Salesman Problem: An overview of exact and approximate algorithms, European Journal of Operational Research, Vol. 59 (1992) 231-247
[2] R. Matai, S. P. Singh, M. L. Mittal, Traveling Salesman Problem: An Overview of Applications, Formulations, and Solution Approaches, in Traveling Salesman Problem, Theory and Applications, InTech, 2010
[3] NP-Problem - from Wolfram MathWorld, http://mathworld.wolfram.com/NP-Problem.html
[4] Zack Grossbart, P Vs. NP: The Assumption That Runs The Internet,
https://www.smashingmagazine.com/2015/11/p-vs-np-assumption-that-runs-internet/
[5] Millenium Problems, Clay Mathematics Instititute,
http://www.claymath.org/millennium-problems
Автор:
Ирена Стојковска, Институт за математика, Природно-математички факултет, Скопје
Објавено на ПОИМ:
25 јули 2017
Начин на цитирање на статијата:
И. Стојковска, Задачата на патувачкиот трговец - едноставна формулација, широка примена, тешка за решавање, Портал ПОИМ на Институтот за математика, ПМФ, Скопје, 25 јули 2017, http://poim-pmf.weebly.com/zadacata-na-patuvackiot-trgovec.html
[1] G. Laporte, The Traveling Salesman Problem: An overview of exact and approximate algorithms, European Journal of Operational Research, Vol. 59 (1992) 231-247
[2] R. Matai, S. P. Singh, M. L. Mittal, Traveling Salesman Problem: An Overview of Applications, Formulations, and Solution Approaches, in Traveling Salesman Problem, Theory and Applications, InTech, 2010
[3] NP-Problem - from Wolfram MathWorld, http://mathworld.wolfram.com/NP-Problem.html
[4] Zack Grossbart, P Vs. NP: The Assumption That Runs The Internet,
https://www.smashingmagazine.com/2015/11/p-vs-np-assumption-that-runs-internet/
[5] Millenium Problems, Clay Mathematics Instititute,
http://www.claymath.org/millennium-problems
Автор:
Ирена Стојковска, Институт за математика, Природно-математички факултет, Скопје
Објавено на ПОИМ:
25 јули 2017
Начин на цитирање на статијата:
И. Стојковска, Задачата на патувачкиот трговец - едноставна формулација, широка примена, тешка за решавање, Портал ПОИМ на Институтот за математика, ПМФ, Скопје, 25 јули 2017, http://poim-pmf.weebly.com/zadacata-na-patuvackiot-trgovec.html
Download (PDF)
Авторизираните статии објавени на Порталот подлежат на законска заштита. Се забранува користење на статиите без наведување на авторот или изворот.