НАУЧНО - ПОПУЛАРНИ СТАТИИСе залагаме за зголемување на свеста за местото и улогата на математиката во науките, технологијата, наставата, природата и културата.
|
Пермутации кај сложувалка со 15 составки
|
Познатата сложувалка со петнаесетте броеви била создадена во 70-тите годинини од XIX век. Нејзин творец бил американецот Сем Лојд, шахист, создавач на загатки и рекреативен математичар. Прашањето предизвикало огромен интерес кај народот, посебно заради наградата од 1000 долари за нејзиното решение. Овој проблем бил детално истражуван од математичарите и обезбедил место во повеќе математички списанија.
|
Вообичаена сложувалката со 15 составки претставува квадрат со 16 полиња. На првите 15 има квадратни парчиња што се нумерирани со броевите од 1 до 15 и соодветно последователно наредени, додека шеснаесеттото е празно. Можно (регуларно) движење на едно квадратно парче е транслатирање (лизгање) на парчето на празното место (тоа е можно ако полето на кое се наоѓа нумерираното парче, како квадрат, има заедничка страна со празното поле). Така, од почетната положба, можни движења се преместувањето на парчето 12 или 15 во празното поле.
Кај познатата сложувалка на Сем Лојд боевите до 12 се последователно наредени, а во последниот ред заменети се местата на 14 и 15, т.е. последователно доаѓаат 13, 15 и 14. Празното поле исто така се наоѓа долу десно.
Кај познатата сложувалка на Сем Лојд боевите до 12 се последователно наредени, а во последниот ред заменети се местата на 14 и 15, т.е. последователно доаѓаат 13, 15 и 14. Празното поле исто така се наоѓа долу десно.
Задачата гласи: Употребувајќи низа од регуларни движења, да им се сменат местата на броевите 14 и 15, така што броевите од 1 до 15 да се последователно наредени.
Во анализата на сложувалката, 16-те квадратни места од сложувалката ги викаме клетки, а 15-те квадратни нумерирани парчиња ги викаме составки. Празното место го сметаме за празна клетка или зафатено со празна составка. Секое регуларно движење се состои во заменување на празното поле со соседна составка која е хоризонтално или вертикално во oднос на него. Конфигурација е биекција од множеството составки (вклучувајќи ја и празната составка) во множеството полиња. Имајќи ја почетната конфигурација, сакаме да дознаеме какви други конфигурации можеме да добиеме употребувајќи низа од регуларни движења. За таа цел, се употребуваат својства на премутациите од множеството составки. Да се потсетиме: пермутација на едно множество M е биективно пресликување од даденото множество само во себе. Множеството од сите пермутации на едно множество е група во однос на операцијата составување на пресликувања. Се означува со SM и се вика симетрична група од пермутации на множеството M. Ако М има n елементи, тогаш симетричната група од пермутации од n елементи ја означуваме со Sn. подолу ќе ги користиме поимите: транспозиција, парна пермутација и алтернативната група пермутации од n елементи, што се познати поими од курсот по Алгебра 2.
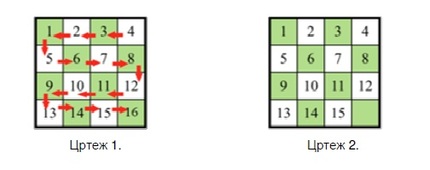
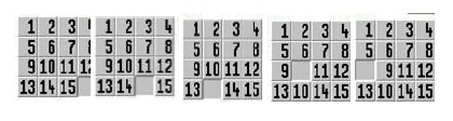
Дефинираме посебно подредување (читање, нумерирање) на клетките (како што е прикажано на цртежот 1 лево). Пермутациите кај сложувалката ќе бидат претставени преку пермутации на клетките, кои се нумерирани на овој начин. Тоа значи дека, транспозицијата (12) ги заменува составките кои се наоѓаат на клетките нумерирани со 1 и 2 (а не составките нумерирани со 1 и 2). Како почетна положба ја сметаме положбата од цртежот 2 (десно). Секој распоред на составките, кои ги читаме според обележаната патека на читање, го викаме конфигурација. Множеството од сите можни конфигурации, независно од тоа каде се наоѓа празната составка, го означувме со G. За секоја конфигурација P∈G дефинираме конфигурација P', во која празната составка се наоѓа на клетката 16. Постојат случаи каде што P=P'. Конфигурацијата P' ја викаме стандардизација на P. Да забележиме дека ако P1 и P2 се конфигурации во G и ако P'1 и P'2 се нивните стандардизации, соодветно, тогаш со низа регуларни движења, може да се стигне од конфигурацијата P1до конфигурацијата P2 ако и само ако со низа од регуларни движења можe да се стигнe од конфигурацијата P'1 до конфигурацијата P'2 .
Во анализата на сложувалката, 16-те квадратни места од сложувалката ги викаме клетки, а 15-те квадратни нумерирани парчиња ги викаме составки. Празното место го сметаме за празна клетка или зафатено со празна составка. Секое регуларно движење се состои во заменување на празното поле со соседна составка која е хоризонтално или вертикално во oднос на него. Конфигурација е биекција од множеството составки (вклучувајќи ја и празната составка) во множеството полиња. Имајќи ја почетната конфигурација, сакаме да дознаеме какви други конфигурации можеме да добиеме употребувајќи низа од регуларни движења. За таа цел, се употребуваат својства на премутациите од множеството составки. Да се потсетиме: пермутација на едно множество M е биективно пресликување од даденото множество само во себе. Множеството од сите пермутации на едно множество е група во однос на операцијата составување на пресликувања. Се означува со SM и се вика симетрична група од пермутации на множеството M. Ако М има n елементи, тогаш симетричната група од пермутации од n елементи ја означуваме со Sn. подолу ќе ги користиме поимите: транспозиција, парна пермутација и алтернативната група пермутации од n елементи, што се познати поими од курсот по Алгебра 2.
Дефинираме посебно подредување (читање, нумерирање) на клетките (како што е прикажано на цртежот 1 лево). Пермутациите кај сложувалката ќе бидат претставени преку пермутации на клетките, кои се нумерирани на овој начин. Тоа значи дека, транспозицијата (12) ги заменува составките кои се наоѓаат на клетките нумерирани со 1 и 2 (а не составките нумерирани со 1 и 2). Како почетна положба ја сметаме положбата од цртежот 2 (десно). Секој распоред на составките, кои ги читаме според обележаната патека на читање, го викаме конфигурација. Множеството од сите можни конфигурации, независно од тоа каде се наоѓа празната составка, го означувме со G. За секоја конфигурација P∈G дефинираме конфигурација P', во која празната составка се наоѓа на клетката 16. Постојат случаи каде што P=P'. Конфигурацијата P' ја викаме стандардизација на P. Да забележиме дека ако P1 и P2 се конфигурации во G и ако P'1 и P'2 се нивните стандардизации, соодветно, тогаш со низа регуларни движења, може да се стигне од конфигурацијата P1до конфигурацијата P2 ако и само ако со низа од регуларни движења можe да се стигнe од конфигурацијата P'1 до конфигурацијата P'2 .
Нека K е множеството од сите конфигурации во кои празната составка е на клетката 16. Множеството од сите регуларни движења го означуваме со L(K). Него го сочинуваат пермутации од обликот (16 i_k-1) (i_k-1 i_k-2) ...(i_2 i_1) (i_1 16) каде што i_j и i_j+1 се соседни клетки за 0 ≤ j < k. Со директна проверка се утврдува дека множеството од сите регуларни движења L(K) заедно со операцијата составување на пресликувања е група.
Преминувајќи од една до друга пермутација, ја движиме празната составка низ клетките, но секогаш ја враќаме на клетката 16. Ако ја поместиме лево, треба да ја вратиме десно; ако ја поместиме горе, треба да ја вратиме долу, т.е. секогаш треба да направиме повторен број на движења.Тоа значи дека секогаш употребуваме парен број движења за да преминеме од една во друга конфигурација, т.е. потребен е парен број транспозиции. Оттука заклучуваме дека не постои непарна пермутација со која, почнувајќи од почетната положба (почетната конфигурација) би стигнале до која било друга конфигурација. Значи, од сите пермутации во Sn, можни се само пермутации што припаѓаат во A_15, па L(K)⊆A_15. Бидејќи L(K) и A_15 се групи, следува дека L(K) е подгрупа од A_15.
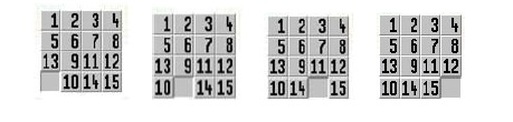
Една транспозиција (i,j) ја реализираме со тоа што ја движиме празната составка од клетката 16 по обележаната патека, сè до првата клетка (од клетките i или j) на која наидуваме. Тогаш ја поместуваме празната составка до втората клетка (i или j) и се враќаме назад до клетката 16, повторно по обележаната патека за движење. Како да се движиме низ сложувалката за да го реализираме движењето (11 14)?
Почнувајќи со празната составка од клетката 16, се движиме по обележаната патека до клетката 14, ја изведуваме транспозицијата и се враќаме по обележаната патека назад до клетката 16. Патеката на празната составка е: 16, 15, 14, 11, 12, 13, 14, 15, 16. На овој начин ја добиваме пермутацијата (16 15)(15 14)(14 13)(13 12)(12 11)(11 14)(14 15)(15 16) = (13 12 11). Оваа пермутација е елемент од L(K) и ја обележуваме со S_11,14.
Преминувајќи од една до друга пермутација, ја движиме празната составка низ клетките, но секогаш ја враќаме на клетката 16. Ако ја поместиме лево, треба да ја вратиме десно; ако ја поместиме горе, треба да ја вратиме долу, т.е. секогаш треба да направиме повторен број на движења.Тоа значи дека секогаш употребуваме парен број движења за да преминеме од една во друга конфигурација, т.е. потребен е парен број транспозиции. Оттука заклучуваме дека не постои непарна пермутација со која, почнувајќи од почетната положба (почетната конфигурација) би стигнале до која било друга конфигурација. Значи, од сите пермутации во Sn, можни се само пермутации што припаѓаат во A_15, па L(K)⊆A_15. Бидејќи L(K) и A_15 се групи, следува дека L(K) е подгрупа од A_15.
Една транспозиција (i,j) ја реализираме со тоа што ја движиме празната составка од клетката 16 по обележаната патека, сè до првата клетка (од клетките i или j) на која наидуваме. Тогаш ја поместуваме празната составка до втората клетка (i или j) и се враќаме назад до клетката 16, повторно по обележаната патека за движење. Како да се движиме низ сложувалката за да го реализираме движењето (11 14)?
Почнувајќи со празната составка од клетката 16, се движиме по обележаната патека до клетката 14, ја изведуваме транспозицијата и се враќаме по обележаната патека назад до клетката 16. Патеката на празната составка е: 16, 15, 14, 11, 12, 13, 14, 15, 16. На овој начин ја добиваме пермутацијата (16 15)(15 14)(14 13)(13 12)(12 11)(11 14)(14 15)(15 16) = (13 12 11). Оваа пермутација е елемент од L(K) и ја обележуваме со S_11,14.
Можни се девет транспозиции, од кои произлегуваат следните пермутации:
S_9,16= (15 14 13 12 11 10 9), S_10,15 = (14 13 12 11 10), S_11,14 = (13 12 11), S_7,10 = (9 8 7),
S_6,11 = (10 9 8 7 6), S_5,12 = (11 10 9 8 7 6 5), S_1,8 = (7 6 5 4 3 2 1), S_2,7 = (6 5 4 3 2) и S_3,6 = (5 4 3).
Анализирајќи ги движењата низ сложувалката на овој начин, работевме во S_16, со оглед на тоа што има 16 клетки и ние ги разместувавме составките што им соодветствуваат заедно со празното место. Бидејќи разгледувавме само конфигурации во кои празната составка е на клетката 16, всушност работевме во S_15. Да се потсетиме, можни се само парни пермутации.
Бидејќи секој елемент од S_n може да се запише како производ од транспозиции од облик (k k+1) и секој елемент од An може да се запише како производ од циклуси со должина 3 од облик (k k+1 k+2), следува дека горната листа пермутации го добива обликот:
S_9,16= (15 14 13 12 11 10 9), S_10,15 = (14 13 12 11 10), S_11,14 = (13 12 11), S_7,10 = (9 8 7),
S_6,11 = (10 9 8 7 6), S_5,12 = (11 10 9 8 7 6 5), S_1,8 = (7 6 5 4 3 2 1), S_2,7 = (6 5 4 3 2) и S_3,6 = (5 4 3).
Анализирајќи ги движењата низ сложувалката на овој начин, работевме во S_16, со оглед на тоа што има 16 клетки и ние ги разместувавме составките што им соодветствуваат заедно со празното место. Бидејќи разгледувавме само конфигурации во кои празната составка е на клетката 16, всушност работевме во S_15. Да се потсетиме, можни се само парни пермутации.
Бидејќи секој елемент од S_n може да се запише како производ од транспозиции од облик (k k+1) и секој елемент од An може да се запише како производ од циклуси со должина 3 од облик (k k+1 k+2), следува дека горната листа пермутации го добива обликот:
Да забележиме дека (3 4 5), (7 8 9) и (11 12 13) ги имаме како инверзни на циклусите формирани од три од транспозициите.
Покажавме дека можни се сите пермутации од облик (k k+1 k+2) и дека сите пермутации од A_n можат да бидат генерирани од ваквите пермутации, т.е. сите пермутации од A_n можат да бидат добиени со низа од регуларни движења. Сепак, почетната конфигурација не мора да биде „природната“ (првата слика лево), туку која било стандардизирана конфигурација, бидејќи секоја стандардизирана конфигурација може да се промени до нејзина еквивалентна конфигурација.
Произволна конфигурација од сложувалката, преку низа регуларни движења може да премине во друга конфигурација ако и само ако нивните стандардизирани форми можат да бидат трансформирани од една во друга, преку парна пермутација.
Загатката што ја поставил Сем Лојд, дали со низа регуларни движења, може да се стигне од конфигурацијата во која на составките нумерирани со 14 и 15 им се сменети местата до почетната конфигурација со „природниот редослед“, има негативен одговор. Таквата цел би се постигнала со транспозицијата (14 15), а бидејќи покажавме дека со низа регуларни движења можеме да реализираме само парни пермутации, бараната конфигурација не е можна.
Извори:
[1] Ѓорѓи Чупона, Бранко Трпеновски, Предавања по алгебра, книга II, Скопје 2000
[2] Аndrew Chapple, Alfonso Croeze, Mhel Lazo, Hunter Merrill, An analysis of the 15-puzzle, 13 pages
[3] Aaron F. Archer, A Modern Treatment of the 15 Puzzle, American Mathematical Monthly 106, 1999, 793799
[4] Keith Conrad, The 15-puzzle (and Rubik’s cube), 11 pages
Автор:
Гордана Николовска, студент на Институт за математика, Природно математички факултет, Скопје
Награден труд (трето место) на 42. Приматијада одржана од 28.04.2015 до 03.05.2015, Балатон во Шиофок, Р. Унгарија.
Ментор: проф. д-р Весна Целакоска-Јорданова
Објавено на ПОИМ:
12 мај 2015
Начин на цитирање на статијата:
Г. Николовска, Пермутации кај сложувалка со 15 составки, Портал ПОИМ на Институтот за математика, ПМФ, Скопје, 12 мај 2015, http://poim-pmf.weebly.com/slozuvalka-so-15-sostavki.html
Покажавме дека можни се сите пермутации од облик (k k+1 k+2) и дека сите пермутации од A_n можат да бидат генерирани од ваквите пермутации, т.е. сите пермутации од A_n можат да бидат добиени со низа од регуларни движења. Сепак, почетната конфигурација не мора да биде „природната“ (првата слика лево), туку која било стандардизирана конфигурација, бидејќи секоја стандардизирана конфигурација може да се промени до нејзина еквивалентна конфигурација.
Произволна конфигурација од сложувалката, преку низа регуларни движења може да премине во друга конфигурација ако и само ако нивните стандардизирани форми можат да бидат трансформирани од една во друга, преку парна пермутација.
Загатката што ја поставил Сем Лојд, дали со низа регуларни движења, може да се стигне од конфигурацијата во која на составките нумерирани со 14 и 15 им се сменети местата до почетната конфигурација со „природниот редослед“, има негативен одговор. Таквата цел би се постигнала со транспозицијата (14 15), а бидејќи покажавме дека со низа регуларни движења можеме да реализираме само парни пермутации, бараната конфигурација не е можна.
Извори:
[1] Ѓорѓи Чупона, Бранко Трпеновски, Предавања по алгебра, книга II, Скопје 2000
[2] Аndrew Chapple, Alfonso Croeze, Mhel Lazo, Hunter Merrill, An analysis of the 15-puzzle, 13 pages
[3] Aaron F. Archer, A Modern Treatment of the 15 Puzzle, American Mathematical Monthly 106, 1999, 793799
[4] Keith Conrad, The 15-puzzle (and Rubik’s cube), 11 pages
Автор:
Гордана Николовска, студент на Институт за математика, Природно математички факултет, Скопје
Награден труд (трето место) на 42. Приматијада одржана од 28.04.2015 до 03.05.2015, Балатон во Шиофок, Р. Унгарија.
Ментор: проф. д-р Весна Целакоска-Јорданова
Објавено на ПОИМ:
12 мај 2015
Начин на цитирање на статијата:
Г. Николовска, Пермутации кај сложувалка со 15 составки, Портал ПОИМ на Институтот за математика, ПМФ, Скопје, 12 мај 2015, http://poim-pmf.weebly.com/slozuvalka-so-15-sostavki.html
Авторизираните статии објавени на Порталот подлежат на законска заштита. Се забранува користење на статиите без наведување на авторот или изворот.