|
НАУЧНО - ПОПУЛАРНИ СТАТИИСе залагаме за зголемување на свеста за местото и улогата на математиката во науките, технологијата, наставата, природата и културата.
|
|
Нерешена мистерија: Низите „зрно град“
|
Скоро 80 години, Collatz-овата хипотеза нити е потврдена, нити е покажано дека не важи. Оваа хипотеза е за еден вид на низи кои едноставно се конструираат. Имено, се почнува од било кој природен број n, и
* ако n е парен, тогаш следниот број е n/2, * ако n е непарен, тогаш следниот број е 3n+1. |
Collatz-овата хипотеза тврди дека независно од почетниот број n, оваа низа ќе стигне до бројот 1, односно секоја ваква низа завршува со бескрен циклус 4, 2, 1, 4, 2, 1, ...
На пример, за n=15, ја добиваме низата
На пример, за n=15, ја добиваме низата
15, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1, 4, 2, 1,...
а за n=21, ја добиваме низата
21, 64, 32, 16, 8, 4, 2, 1, 4, 2, 1,...
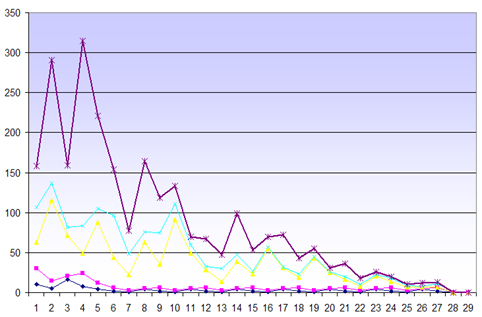
Вредностите на елементите на овие низи варираат горе, долу, како и зрната град во облаците пред да паднат на земјата. Од таму е и името на овие низи, како низи „зрно град“ (hailstone sequences). Од кој број и да пробате да почнете, изгледа дека ќе мора да завршите со бескрајниот циклус 4, 2, 1, 4, 2, 1,...Токму во ова се состои и Collatz-овата хипотеза, предложена од Lothar Collatz во 1937 година, според која независно од почетниот број n, низата „зрно град“ ќе стигне до бројот 1. Оваа хипотеза позната е и под името 3n+1 хипотеза.
|
До сега, со помош на компјутер, испитана е Collatz-овата хипотеза за сите почетни броеви до 5 × 2^60 ≈ 5.764×10^18 (Tomás Oliveira e Silva, "Computational verification of the 3x+1 conjecture") и добиено е дека секоја од низите завршува со бескрајниот циклус 4, 2, 1, 4, 2, 1,... Но, ова не е потврда дека Collatz-овата хипотеза важи, имено може да постои доволно голем број за кој таа не важи. Таков бил случајот со некои од познатите хипотези, како на пример Pólya-вата хипотеза, Mertens-овата хипотеза и слично, кои долго време не биле решени, или било докажано дека не важат, но било потребно подолго време да се најде доволно голем број за кој хипотезата не важи, односно да се најдеконтрапример.
|
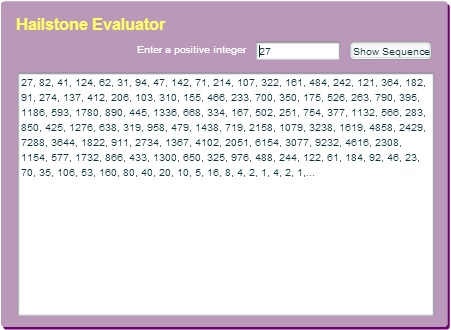
Пресметувач на низите „зрно град“ (Hailstone Evaluator), https://plus.maths.org/content/mathematical-mysteries-hailstone-sequences
|
Од друга страна, има истражувачи кои се обидуваат да најдат математички доказ за точноста на Collatz-овата хипотеза, или да докажат дека не важи, со тоа што би покажале дека постои бесконечно растечка низа од овие броеви или дека постои низа од овие броеви која завршува со некој друг бескраен циклус кој не го содржи бројот 1. Постојат голем број на трудови со вакви обиди, но никој од нив се уште не е признаен дека го има решено Collatz-овиот проблем ([3], [4]). Не случајно Paul Erdős има изјавено во врска со Collatz-овата хипотеза: Математиката се уште не е спремна за ваков вид на проблеми.
Имено, се верува дека математичкиот доказ на Collatz-овата хипотеза треба да роди нови математички теории, кои би довеле до нови корисни резултати во повеќе области на математката. Проблемот не е дали хипотезата е точна или не, туку како би изгледал тој доказ.
Извори:
[1] Mathematical mysteries: Hailstone sequences
[2] Tomás Oliveira e Silva, "Computational verification of the 3x+1 conjecture"
[3] Gerhard Opfer, An analytic approach to the Collatz 3n + 1 Problem
[4] Peter Schorer, A Solution to the 3x + 1 Problem
[5] Matthew Hammett, The Collatz Conjecture: A Brief Overview
[6] Project Euler Problem 14: Hailstone Numbers
Автор:
Ирена Стојковска, Институт за математика, Природно-математички факултет, Скопје
Објавено на ПОИМ:
21 август 2015
Начин на цитирање на статијата:
И. Стојковска, Нерешена мистерија: Низите „зрно град“, Портал ПОИМ на Институтот за математика, ПМФ, Скопје, 21 август 2015, http://poim-pmf.weebly.com/nizite-zrno-grad.html
Имено, се верува дека математичкиот доказ на Collatz-овата хипотеза треба да роди нови математички теории, кои би довеле до нови корисни резултати во повеќе области на математката. Проблемот не е дали хипотезата е точна или не, туку како би изгледал тој доказ.
Извори:
[1] Mathematical mysteries: Hailstone sequences
[2] Tomás Oliveira e Silva, "Computational verification of the 3x+1 conjecture"
[3] Gerhard Opfer, An analytic approach to the Collatz 3n + 1 Problem
[4] Peter Schorer, A Solution to the 3x + 1 Problem
[5] Matthew Hammett, The Collatz Conjecture: A Brief Overview
[6] Project Euler Problem 14: Hailstone Numbers
Автор:
Ирена Стојковска, Институт за математика, Природно-математички факултет, Скопје
Објавено на ПОИМ:
21 август 2015
Начин на цитирање на статијата:
И. Стојковска, Нерешена мистерија: Низите „зрно град“, Портал ПОИМ на Институтот за математика, ПМФ, Скопје, 21 август 2015, http://poim-pmf.weebly.com/nizite-zrno-grad.html
Авторизираните статии објавени на Порталот подлежат на законска заштита. Се забранува користење на статиите без наведување на авторот или изворот.
