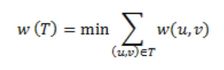НАУЧНО - ПОПУЛАРНИ СТАТИИСе залагаме за зголемување на свеста за местото и улогата на математиката во науките, технологијата, наставата, природата и културата.
|
МРЕЖНО ПРОГРАМИРАЊЕ
- проблем на минимално опфаќачко дрво, Примов алгоритам и негова примена на конкретен проблем
|
Поимот за мрежи често се среќава во секојдневниот живот. Мрежните претставувања наоѓаат широка примена во производството, транспортот, инфраструктурните планови, комуникацијата и дистрибуцијата. Со помош на мрежна оптимизација се одредуваат и оптимални планови за поставување на телефонски жици и далеководи, мрежно поврзување на електронски уреди со минимизирање на должината на искористените кабли, оптимален план за изградба на железници и патишта, итн. Поради широката примена и високата ефикасност на визуелизација на врските помеѓу одредени делови од еден систем, мрежите се користат во скоро секое поле од науката и економијата.
|
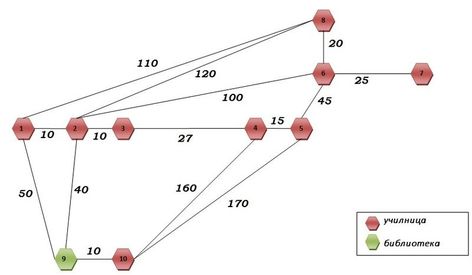
Институтот за математика на Природно-математичкиот факултет во Скопје, располага со еден амфитеатар, осум предавални и една библиотека (Слика 1). Проблемот на најекономично поврзување на сите овие простории во една мрежа е предмет од полето на Теорија на графови и полето на Мрежна оптимизација. Имено, овој проблем може да се класифицира како проблем на минимално опфаќачко дрво (minimum spanning tree problem). Минимално опфаќачко дрво се дефинира како начин на поврзување на сите темиња во една мрежа со искористување на најмала можна „тежина“, ако секој раб е зададен со определена „тежина“ (во нашиот случај должина).
Слика 1. Просториите со кои располага Институтот за математика и кои се предмет на поврзување со мрежа
1. Основни поими од теоријата на графови
Под мрежа подразбираме подреден пар од темиња (V) и рабови (E), т.е. G = (V, E). Разликaтa помеѓу различни типови мрежи е токму во дефинираноста на множеството Е. Во насочени мрежи, секој елемент од множеството Е претставува подреден пар, а рабовите ги замислуваме како стрелки од едно, почетно теме, до друго, крајно теме. Во ненасочени мрежи, секој раб претставува двоелементно подмножество на V. Едноставна ненасочена мрежа не содржи повеќе од еден раб меѓу ист пар темиња, ниту пак јамки („рабови“ кои поврзуваат едно теме само со себе). Под циклус подразбираме мрежа за која важи дека за n темиња {0, 1, 2, ..., n-1} постои раб помеѓу i и i+1 за секое i = 0, 1, 2, … n-1 и помеѓу 0 и n-1. Мрежа која не содржи циклуси се нарекува ациклична мрежа.
2. Минимално опфаќачко дрво
Со помош на овие поими и поделби на мрежите, можеме да дојдеме до поимот дрво, под кој подразбираме една ациклична, поврзана мрежа. Опфаќачко дрво во една мрежа G е подмрежа од G која ги содржи (ги опфаќа) сите темиња, и сама по себе претставува дрво. Нашиот проблем, најекономично мрежно поврзување на просториите на Институтот за математика, го измоделиравме како проблем на минимално опфаќачко дрво. Како што индицира самиот наслов, овој проблем налага формирање на опфаќачко дрво во една дадена мрежа G = ( V, E) во која секој од рабовите (u, v) има своја т.н. тежина w(u, v) (која може да претставува каква било особина, а во нашиот случај должина), така што вкупната тежина да биде минимална. Значи, бараме подмножество T од множеството рабови E (во нашиот случај патишта), така што за функцијата на тежина имаме
Под мрежа подразбираме подреден пар од темиња (V) и рабови (E), т.е. G = (V, E). Разликaтa помеѓу различни типови мрежи е токму во дефинираноста на множеството Е. Во насочени мрежи, секој елемент од множеството Е претставува подреден пар, а рабовите ги замислуваме како стрелки од едно, почетно теме, до друго, крајно теме. Во ненасочени мрежи, секој раб претставува двоелементно подмножество на V. Едноставна ненасочена мрежа не содржи повеќе од еден раб меѓу ист пар темиња, ниту пак јамки („рабови“ кои поврзуваат едно теме само со себе). Под циклус подразбираме мрежа за која важи дека за n темиња {0, 1, 2, ..., n-1} постои раб помеѓу i и i+1 за секое i = 0, 1, 2, … n-1 и помеѓу 0 и n-1. Мрежа која не содржи циклуси се нарекува ациклична мрежа.
2. Минимално опфаќачко дрво
Со помош на овие поими и поделби на мрежите, можеме да дојдеме до поимот дрво, под кој подразбираме една ациклична, поврзана мрежа. Опфаќачко дрво во една мрежа G е подмрежа од G која ги содржи (ги опфаќа) сите темиња, и сама по себе претставува дрво. Нашиот проблем, најекономично мрежно поврзување на просториите на Институтот за математика, го измоделиравме како проблем на минимално опфаќачко дрво. Како што индицира самиот наслов, овој проблем налага формирање на опфаќачко дрво во една дадена мрежа G = ( V, E) во која секој од рабовите (u, v) има своја т.н. тежина w(u, v) (која може да претставува каква било особина, а во нашиот случај должина), така што вкупната тежина да биде минимална. Значи, бараме подмножество T од множеството рабови E (во нашиот случај патишта), така што за функцијата на тежина имаме
Тежината на рабовите е секогаш позитивен број. Една мрежа може да има повеќе различни опфаќачки дрва, а од сите нив, оптимално решение на проблемот на минимално опфаќачко дрво е она кое има помала или еднаква вкупна тежина во споредба со сите останати опфаќачки дрва во мрежата. Од самата дефиниција и својствата за дрво во една мрежа, гледаме дека во овој проблем ни се потребни точно n – 1 врски. Всушност, нашиот проблем ќе го решиме, ако одредиме точно 9 парови од простории меѓу кои треба да се пратат кабли, за сите наши 10 простории да бидат мрежно поврзани на оптимален начин.
3. Примов алгоритам
Во продолжение ќе разгледаме еден од алгоритмите за наоѓање на тие врски и индуцирање на оптимално решение на конкретниот проблем, познат под името Примов алгоритам, кој името го добил според Robert Clay Prim.
Да претпоставиме дека дадена ни е една поврзана, ненасочена мрежа G = (V, E) со функција на тежина w: E → R. Целта ни е да најдеме минимално опфаќачко дрво за G. Примовиот алгоритам е таканаречен алчен алгоритам (greedy algorithm). Ова значи дека опфаќачкото дрво се „разгранува“ постапно, избирајќи ги темињата еднo по еднo. Алгоритамот работи со едно множество А, така што во цуклусот важи инваријантата: Пред секоја итерација, А е подмножество од некое минимално опфаќачко дрво. Во секој чекор избираме по еден раб (u, v) кој смее да се додаде на множеството А, без при тоа да се наруши инваријантата, односно А U {(u, v)} е исто така подмножество од некое минимално опфаќачко дрво. Ваквиот раб го нарекуваме безбеден раб за А, бидејќи тој безбедно може да се додаде на множеството А и при тоа да важи инваријантата (Алгоритам 1).
3. Примов алгоритам
Во продолжение ќе разгледаме еден од алгоритмите за наоѓање на тие врски и индуцирање на оптимално решение на конкретниот проблем, познат под името Примов алгоритам, кој името го добил според Robert Clay Prim.
Да претпоставиме дека дадена ни е една поврзана, ненасочена мрежа G = (V, E) со функција на тежина w: E → R. Целта ни е да најдеме минимално опфаќачко дрво за G. Примовиот алгоритам е таканаречен алчен алгоритам (greedy algorithm). Ова значи дека опфаќачкото дрво се „разгранува“ постапно, избирајќи ги темињата еднo по еднo. Алгоритамот работи со едно множество А, така што во цуклусот важи инваријантата: Пред секоја итерација, А е подмножество од некое минимално опфаќачко дрво. Во секој чекор избираме по еден раб (u, v) кој смее да се додаде на множеството А, без при тоа да се наруши инваријантата, односно А U {(u, v)} е исто така подмножество од некое минимално опфаќачко дрво. Ваквиот раб го нарекуваме безбеден раб за А, бидејќи тој безбедно може да се додаде на множеството А и при тоа да важи инваријантата (Алгоритам 1).
Алгоритам 1. Генерирачки алгоритам за минимално опфаќачко дрво
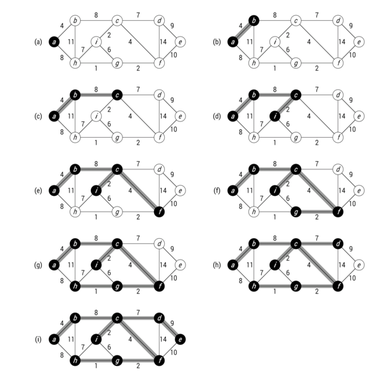
Примовиот алгоритам работи на принципот: во секој момент, рабовите во множеството А формираат единствено дрво. На Слика 2 сликовито е образложен овој принцип. Првото теме, или „коренот“ на дрвото во овој случај е a. Задебелените рабови се оние врски кои влегуваат во опфаќачкото дрво кое расте, а сите рабови во мрежата се прикажани со црни линии. Во секој чекор од алгоритамот, темињата во дрвото определуваат еден пресек на мрежата, и еден лесен раб кој го прекршува пресекот се додава на дрвото. Во вториот чекор, на пример, алгоритамот има избор дали да го додаде работ (b, c) или работ (a, h) на дрвото бидејќи и двата се лесни рабови што го прекршуваат пресекот.
Слика 2. Развивање на Примовиот алгоритам прикажано на произволна мрежа.
4. Оптимално мрежно поврзување на просториите од Институтот за математика
При решавање на нашиот проблем, оптимално мрежно поврзување на просториите од Институтот за математика, дрвото започнува од една произволна просторија x елемент од {1,2,…,10}, и понатаму продолжува да се разгранува сé додека не ги опфати сите простории. Овде зборуваме за алчна стратегија, бидејќи во секој чекор, дрвото се надополнува со нов раб, или му се додава нов пат помеѓу две простории кој вкупната должина која влегува во „тежината“ на дрвото ја надополнува со најкратка можна должина. Клучниот дел во ефикасното развивањето на Примовиот алгоритам е да се олесни избирањето на нов раб кој ќе се додаде на дрвото А.
На Слика 1, просториите на Институтот за математика ни се претставени со мрежа, каде што секое од нумерираните темиња претставува по една просторија: со црвени шестаголници претставени се сите училници, а со зелен шестаголник е претставена математичката библиотека. На секој раб запишан е по еден број (рабовите се всушност најлогичните патишта, измерено низ ходници и скали), а броевите ги претставуваат растојанијата помеѓу соодветните простории во метри (Забелешка: на сликата се претставени приближните должини помеѓу просториите).
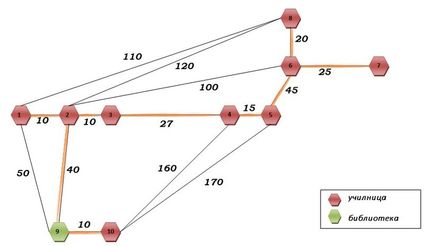
По примената на Примовиот аглоритам на овој проблем, дојдовме до оптималното решение коешто нам ни е од интерес, начинот на кој може да се поврзат сите барани простории, за притоа да се искористи најкраток кабел и најмалку материјал (Слика 3). Со жолти линии се обележани патиштата помеѓу секои две простории кои е доволно да бидат меѓу себе директно поврзани, за на крај да добиеме мрежа која ги опфаќа сите 10 простории.
При решавање на нашиот проблем, оптимално мрежно поврзување на просториите од Институтот за математика, дрвото започнува од една произволна просторија x елемент од {1,2,…,10}, и понатаму продолжува да се разгранува сé додека не ги опфати сите простории. Овде зборуваме за алчна стратегија, бидејќи во секој чекор, дрвото се надополнува со нов раб, или му се додава нов пат помеѓу две простории кој вкупната должина која влегува во „тежината“ на дрвото ја надополнува со најкратка можна должина. Клучниот дел во ефикасното развивањето на Примовиот алгоритам е да се олесни избирањето на нов раб кој ќе се додаде на дрвото А.
На Слика 1, просториите на Институтот за математика ни се претставени со мрежа, каде што секое од нумерираните темиња претставува по една просторија: со црвени шестаголници претставени се сите училници, а со зелен шестаголник е претставена математичката библиотека. На секој раб запишан е по еден број (рабовите се всушност најлогичните патишта, измерено низ ходници и скали), а броевите ги претставуваат растојанијата помеѓу соодветните простории во метри (Забелешка: на сликата се претставени приближните должини помеѓу просториите).
По примената на Примовиот аглоритам на овој проблем, дојдовме до оптималното решение коешто нам ни е од интерес, начинот на кој може да се поврзат сите барани простории, за притоа да се искористи најкраток кабел и најмалку материјал (Слика 3). Со жолти линии се обележани патиштата помеѓу секои две простории кои е доволно да бидат меѓу себе директно поврзани, за на крај да добиеме мрежа која ги опфаќа сите 10 простории.
Слика 3. Оптимално решение на нашиот проблем.
Програмата која го решава проблемот на минимално опфаќачко дрво во општ случај со помош на Примовиот алгоритам ја изработивме во програмскиот јазик Visual Basic. Таа содржи дел кој го објаснува концептот на минимално опфаќачко дрво и Примовиот алгоритам, нуди опција за примена на овој алгоритам на произволна мрежа и ни ги излага пресметките извршени за добивање на ова оптимално решение на нашиот проблем.
Кон целосниот труд „Мрежно програмирање – проблем на минимално опфаќачко дрво, Примов алгоритам и негова примена на конкретен проблем“ презентиран на Приматијадата 2015 (Балатон, Унгарија) може да пристапите тука.
Извори:
[1] Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein, INTRODUCTION TO ALGORITHMS, Second Edition, The MIT Press, 2001
[2] F. S. Hillier, G. J. Lieberman, INTRODUCTION TO OPERATIONS RESEARCH, Seventh Edition, The McGraw-Hill Book Company, 2001
[3] James Aspnes, NOTES ON GRAPH THEORY, Yale University, December 2010
Автор:
Ивона Ѓероска, студент на Институт за математика, Природно математички факултет, Скопје
Награден труд (второ место) на 42. Приматијада одржана од 28.04.2015 до 03.05.2015, Балатон во Шиофок, Р. Унгарија
Ментор: доц. д-р Ирена Стојковска
Објавено на ПОИМ:
14 мај 2015
Начин на цитирање на статијата:
И. Ѓероска, Мрежно програмирање - Проблем на минимално опфаќачко дрво, Примов алгоритам и негова примена на конкретен проблем, Портал ПОИМ на Институтот за математика, ПМФ, Скопје, 14 мај 2015, http://poim-pmf.weebly.com/mrezno-programiranje.html
Кон целосниот труд „Мрежно програмирање – проблем на минимално опфаќачко дрво, Примов алгоритам и негова примена на конкретен проблем“ презентиран на Приматијадата 2015 (Балатон, Унгарија) може да пристапите тука.
Извори:
[1] Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein, INTRODUCTION TO ALGORITHMS, Second Edition, The MIT Press, 2001
[2] F. S. Hillier, G. J. Lieberman, INTRODUCTION TO OPERATIONS RESEARCH, Seventh Edition, The McGraw-Hill Book Company, 2001
[3] James Aspnes, NOTES ON GRAPH THEORY, Yale University, December 2010
Автор:
Ивона Ѓероска, студент на Институт за математика, Природно математички факултет, Скопје
Награден труд (второ место) на 42. Приматијада одржана од 28.04.2015 до 03.05.2015, Балатон во Шиофок, Р. Унгарија
Ментор: доц. д-р Ирена Стојковска
Објавено на ПОИМ:
14 мај 2015
Начин на цитирање на статијата:
И. Ѓероска, Мрежно програмирање - Проблем на минимално опфаќачко дрво, Примов алгоритам и негова примена на конкретен проблем, Портал ПОИМ на Институтот за математика, ПМФ, Скопје, 14 мај 2015, http://poim-pmf.weebly.com/mrezno-programiranje.html
Download (PDF)
Авторизираните статии објавени на Порталот подлежат на законска заштита. Се забранува користење на статиите без наведување на авторот или изворот.