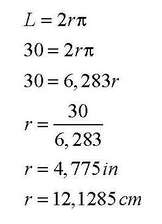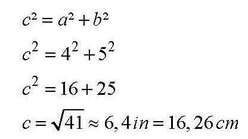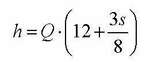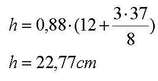СТАТИИ ОД МЕСЕЦОТ НА НАУКАТАСе залагаме за зголемување на свеста за местото и улогата на математиката во науките, технологијата, наставата, природата и културата.
|
Математика во модниот дизајн

Математиката е наука која има примена во секое поле. Таа е дел од нашето секојдневие, како и дел од останатите науки и области. Низ овој текст ќе можете да дознаете за уште едно од многуте полиња каде математиката наоѓа примена.
Со нејзината огромна примена, математиката има голем удел и во дизајнирањето и модниот дизајн. Модните дизајнери употребуваат голем дел од математиката, почнувајќи од наједноставните пресметки и формули, па се до посложени проблеми од аритметика, алгебра, геометрија.
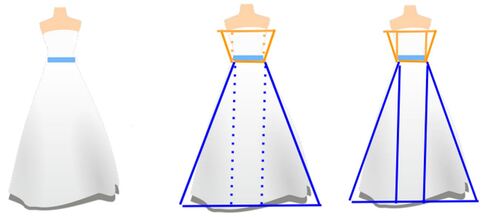
За да може облеката која ја носиме правилно да се вклопува на нас, дизајнерот треба да знае:
Со нејзината огромна примена, математиката има голем удел и во дизајнирањето и модниот дизајн. Модните дизајнери употребуваат голем дел од математиката, почнувајќи од наједноставните пресметки и формули, па се до посложени проблеми од аритметика, алгебра, геометрија.
За да може облеката која ја носиме правилно да се вклопува на нас, дизајнерот треба да знае:
- Најпрво прецизно да ја нацрта скицата на моделот кој треба да се изработува;
- Презицизно да ги измери потребните агли и големини;
- Да ги изврши правилно пресметките;
- Да користи шаблони изработени од хартија со цел полесно да го преслика парчето облека кое треба да се сошие;
- Да изработи облека која ќе одговара на луѓе со различни пропорции.
За да може облеката која ја носиме правилно да се вклопува на нас, дизајнерот треба да знае:
- Најпрво прецизно да ја нацрта скицата на моделот кој треба да се изработува;
- Презицизно да ги измери потребните агли и големини;
- Да ги изврши правилно пресметките;
- Да користи шаблони изработени од хартија со цел полесно да го преслика парчето облека кое треба да се сошие;
- Да изработи облека која ќе одговара на луѓе со различни пропорции.
Модните дизајнери употребуваат голем дел од математиката, почнувајќи од наједноставните пресметки и формули, па сѐ до посложени проблеми од аритметика, алгебра, геометрија.
Еден од добро познатите примери во кои се употребува математика е примерот при формирањето на цената на готовите производи. Тоа се заснова на:
- Износот пари којшто дизајнерот го потрошил за да ја изработи облеката;
- Колкумина од луѓето ќе го купат парчето облека;
- Колку ќе треба да платат луѓето за да го купат парчето облека;
- Заработката на дизајнерот ќе се пресмета на тој начин што доколку од цената која ја платил купувачот ја одземеме цената којашто ја платил дизајнерот за да го сошие.
Меѓутоа, ова не е единствениот пример каде математиката наоѓа примена во модниот дизајн. Многу повеќе за нејзината примена може да согледаме преку следниве неколку примери
Пример 1: Едноставен дизајн на фустан со употреба на 2Д-форми
Во овој пример имаме речиси наједноставна употреба на геометрија. Тоа дизајнерот го постигнал со употреба на едноставни 2Д форми како: квадрати, триаголници, правоаголници, паралелограми, како и употреба и на неправилни четириаголници и фигури.
Во овој пример имаме речиси наједноставна употреба на геометрија. Тоа дизајнерот го постигнал со употреба на едноставни 2Д форми како: квадрати, триаголници, правоаголници, паралелограми, како и употреба и на неправилни четириаголници и фигури.
Пример 2: Необични дизајни на фустани со употреба на 3Д форми
Некои дизајнери обидувајќи се да создадат поинтересни дизајни, се сетиле дека покрај едноставната употреба на 2Д форми, би можеле да употребат и 3Д форми со цел да создадат поразлични дизајни кои ќе привлечат повеќе внимание.
Интересно е и тоа што овие 3Д форми покрај употребата кај овие необични дизајни на фустани се употребуваат и при изработката на накит, секако, со цел, создавање на уникатен и привлечен дизајн. Тоа лесно можеме да го забележиме низ следните фотографии:
Пример 3: Формирање кружно здолниште и употреба на формула за периметар и плоштина на круг
Материјалот е преклопен на 4 дела. Треба да го пресметаме радиусот на отворот кој треба да го направиме за околу половината. Најпрво треба да за измери обемот на половината (во примерот 30 инчи, или 76.2 сантиметри). За да го најдеме радиусот, заменуваме знаејќи ја формулата за периметар на круг.
Според тоа, радиусот на отворот ќе биде 12,1 cm, додека за дожината на здолништето можеме самите да одлучиме. Исто така, откако ќе се формира здолништето, можеме да ја пресметаме и неговата плоштина така што прво ќе ја пресметаме плоштина на големиот, а потоа од него ја одземеме плоштината на малиот круг т.е. P=(R² - r²)π, каде R е радиусот на големиот круг, а r е радиусот на малиот круг. При тоа, R - r е должината на здолништето.
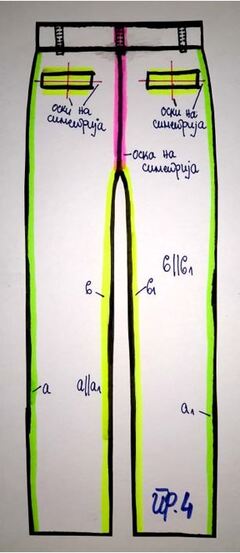
Пример 4: Употреба на симетричност и паралелни линии
При дизајнирањето облека како што се маици, блузи, панталони и слично, многу е важен начинот на кои се конструирани. Спротивните страни треба да бидат паралелни, во спротивно нема правилно да лежат на нашето тело.
При дизајнирањето облека како што се маици, блузи, панталони и слично, многу е важен начинот на кои се конструирани. Спротивните страни треба да бидат паралелни, во спротивно нема правилно да лежат на нашето тело.
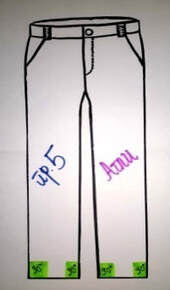
Пример 5: Употреба на правите агли и Питагорова теорема
При изработката на облеката, аглите се многу важни. Така на пример при изработката на панталони, долниот дел многу е важно да биде под прав агол, во спротивно тие ќе бидат нерамни.
Аглите исто така се важни и кај отворот на блузи, маици и слични парчиња облека кои имаат V-отвор.Тој треба да биде околу 90°, зашто во спротивно, отворот ќе биде многу мал, или, пак, тоа може да зависи и од видот на материјалот од кој се изработува.
При изработката на облеката, аглите се многу важни. Така на пример при изработката на панталони, долниот дел многу е важно да биде под прав агол, во спротивно тие ќе бидат нерамни.
Аглите исто така се важни и кај отворот на блузи, маици и слични парчиња облека кои имаат V-отвор.Тој треба да биде околу 90°, зашто во спротивно, отворот ќе биде многу мал, или, пак, тоа може да зависи и од видот на материјалот од кој се изработува.
Иако никогаш не би помислиле дека е така, сепак при дизајнирањето на високите потпетици, дизајнерите користат една многу позната теорема: Питагоровата теорема.
На пример, доколку дизајнерот одлучи дека сака потпетицата да биде висока 4 инчи (10,16 cm), а просторот помеѓу потпетицата и базата, т.е. просторот од потпетицата до предниот дел да биде 5 инчи (12,7 cm), тогаш треба да знае да ја пресмета хипотенузата на правоаголниот триаголник којшто се формира. За да се направи тоа, треба да се искористи Питагоровата теорема која важи само за правоаголен триаголник. Така, хипотенузата c на правоаголен триаголник со катети a = 4 инчи и b = 5 инчи e:
Во институтот по физика во Лондон измислиле формула со која ќе може да се пресмета максималната големина на потпетица која одговара со бројот на чевли.
Притоа, h е максимална висина на потпетицата (во cm), Q e социолошки фактор и има вредност помеѓу 0 и 1 (се добива на посложен начин и е резултат на некои мерења и вредности), а s е големина на чевлите. Така на пример, ако социолошкиот фактор изнесува 0,88 и бројот на чевли е 37, тогаш добиваме дека максималната висина на потпетиците треба да биде 22,77 cm.
Пример 6: Потребата за правилна конструкција на отворот кај ракавите и вратот на облеката
Обемот и правилната конструкција на кружните отвори на ракавите и отворот околу вратот е многу важна при дизајнирањето облека. На пример, при изработката на ракавите на фустан дизајнерот треба да знае како правилно да го измери обемот на раката на моделот. Во спротивно, облеката ќе биде многу неудобна. Треба да се внимава да не бидат премногу тесни, но воедно и не премногу широки.
Обемот и правилната конструкција на кружните отвори на ракавите и отворот околу вратот е многу важна при дизајнирањето облека. На пример, при изработката на ракавите на фустан дизајнерот треба да знае како правилно да го измери обемот на раката на моделот. Во спротивно, облеката ќе биде многу неудобна. Треба да се внимава да не бидат премногу тесни, но воедно и не премногу широки.
Пример 7: Дизајн на облека со карирани линии
Дизајнерите користат и дизајн со карирани линии, односно тој се состои од паралелни линии поставени хоризонтално и вертикално, под прави агли, на тој начин што формираат квадрати или правоаголници.
Овој дизајн е формиран на следниов начин:
Дизајнерите користат и дизајн со карирани линии, односно тој се состои од паралелни линии поставени хоризонтално и вертикално, под прави агли, на тој начин што формираат квадрати или правоаголници.
Овој дизајн е формиран на следниов начин:
- Се формира група паралелни линии кои одат вертикално, додека другата група оди хоризонтално. Се формираат прави агли и линии во четири правци, се формира правоаголник.
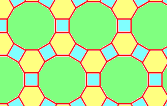
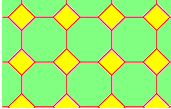
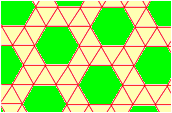
Пример 8: Примена на тесалацијата
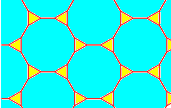
Една од геометриските трансформации е тесалацијата. Тесалација претставува повторување на една или повеќе фигури во рамнината без преклопување. Карактеристично за оваа геометриска трансформација е тоа што аглите на фигурите околу која било точка секогаш даваат збир од 360°. Покрај тесалација на едноставни фигури како триаголници, квадрати и правоаголници, може да се изврши тесалација и на посложени фигури, а со тоа да се добие интересен и уникатен дизајн.
Една од геометриските трансформации е тесалацијата. Тесалација претставува повторување на една или повеќе фигури во рамнината без преклопување. Карактеристично за оваа геометриска трансформација е тоа што аглите на фигурите околу која било точка секогаш даваат збир од 360°. Покрај тесалација на едноставни фигури како триаголници, квадрати и правоаголници, може да се изврши тесалација и на посложени фигури, а со тоа да се добие интересен и уникатен дизајн.
Низ следните неколку фотографии јасно можеме да ја забележиме употребата на тесалацијата при дизајнирањето облека, како со помош на едноставни, така и со посложени и покомплицирани фигури.
- Кај овој фустан дизајнерот употребил тесалација на триаголници, со цел да добие уникатен дизајн.
- Во следните два примери имаме едноставни дизајни формирани со помош на повторување на само една фигура.
- Кај овие дизајни можеме да забележиме дека за нив е употребена исто така тесалацијата, меѓутоа, на малку посложени фигури.
Пример 9: Дизајн со повторување на квадрати, ромбови и паралелограми
Argyle (Аргил) - дизајн кој можеме да го сретнеме на многу џемпери и претставува одличен пример за примената на геометријата во модниот дизајн. Се формира на тој начин што најпрво се цртаат квадратите (или ромбовите) на шаблонот. Потоа се цртаат паралелни прави низ средините на соодветните страни на квадратите, односно ромбовите. Кога овие прави се сечат тие формираат помали и поголеми квадрати, односно ромбови. Затоа овој дизајн всушност претставува серија ромбови коишто се преклопуваат.
Argyle (Аргил) - дизајн кој можеме да го сретнеме на многу џемпери и претставува одличен пример за примената на геометријата во модниот дизајн. Се формира на тој начин што најпрво се цртаат квадратите (или ромбовите) на шаблонот. Потоа се цртаат паралелни прави низ средините на соодветните страни на квадратите, односно ромбовите. Кога овие прави се сечат тие формираат помали и поголеми квадрати, односно ромбови. Затоа овој дизајн всушност претставува серија ромбови коишто се преклопуваат.
Пример 10: Примена на формула за периметар и плоштина на триаголник и правоаголник
Дизајнерот изработува фустан. За да го изработи потребно му е платно. Најпрво треба да знае колку платно му е потребно. За таа цел тој парчето платно го дели на група помали парчиња,триаголници и правоаголници а потоа ја пресметува плоштината на секоја фигура. Во нашиот случај се триаголници и правоаголници со цел рационално искористување на парчето платно за што помалку отпадок. Плоштината на правоаголникот ја пресметуваме по формулата P = ab (должина по ширина), а на триаголникот по формулата P = ah/2. Со собирање на плоштините се добива вкупната плоштина на материјалот искористен за изработка на фустанот. (Од сликата забележуваме дека со самото формирање на триаголници и правоаголници, се формира трапез, така што исто така може да биде искористена и формулата за пресметување плоштина на трапез P = (a+b)h/2, каде што a и b се основите на трапезот а h висината односно растојанието мегу основите на трапезот). Секако, на овој или на оној начин, тој ќе ја пресмета плоштина само на материјалот кој ќе биде потребен за да се изработи фустанот. Меѓутоа, при купувањето, тој ќе мора да купи повеќе материјал, при што оттаму ќе потроши точно толку материјал колку што му е потебно за да го изработи фустанот, но со тоа ќе добие и мали парчиња, остатоци и воедно, ќе мора да ги плати и нив.
Дизајнерот изработува фустан. За да го изработи потребно му е платно. Најпрво треба да знае колку платно му е потребно. За таа цел тој парчето платно го дели на група помали парчиња,триаголници и правоаголници а потоа ја пресметува плоштината на секоја фигура. Во нашиот случај се триаголници и правоаголници со цел рационално искористување на парчето платно за што помалку отпадок. Плоштината на правоаголникот ја пресметуваме по формулата P = ab (должина по ширина), а на триаголникот по формулата P = ah/2. Со собирање на плоштините се добива вкупната плоштина на материјалот искористен за изработка на фустанот. (Од сликата забележуваме дека со самото формирање на триаголници и правоаголници, се формира трапез, така што исто така може да биде искористена и формулата за пресметување плоштина на трапез P = (a+b)h/2, каде што a и b се основите на трапезот а h висината односно растојанието мегу основите на трапезот). Секако, на овој или на оној начин, тој ќе ја пресмета плоштина само на материјалот кој ќе биде потребен за да се изработи фустанот. Меѓутоа, при купувањето, тој ќе мора да купи повеќе материјал, при што оттаму ќе потроши точно толку материјал колку што му е потебно за да го изработи фустанот, но со тоа ќе добие и мали парчиња, остатоци и воедно, ќе мора да ги плати и нив.
Ова се примери со примена на математиката во само едно од огромниот број полиња од секојдневниот живот.
Секоја наука е базирана на математиката, така што секој дел од нејзиното познавање ќе го употребиме еден ден, дури и да не го забележиме тоа. Доколку малку подобро погледнеме, ќе сфатиме, дека всушност, таа е НАСЕКАДЕ околу нас.
Користена литература:
[1] П. Винтерс, П. Кивлин, С. Пембертон, Математика за VIII одд., Арс Ламина, Скопје, 2016
[2] П. Винтерс, П. Кивлин, С. Пембертон, Математика за IX одд., Арс Ламина, Скопје, 2016
[3] Jovan Trajkovic, Mаjstor amater, krojenje i sivanje, Prakticna knjiga, Beograd, 1984
[4] Johan C. Bertoletti, Math in the Real World, How Fashion Designers Use Math, Infobase Publishing, 2010.
[5] Fashion Designer, https://www.math.uci.edu/mathceo/Files/Career_presentations/Fashion_Designer.pdf
[6] When Fashion Meets Geometry, Molempire, Fashion, December 1, 2010
Автор:
Елена Петковска IXв одд., ООУ„Страшо Пинџур“ - Неготино
Награден експеримент со прва награда на Ноември - Месец на науката 2018 во категоријата 7-9 одд.
Професор:
Силвана Миладинова
Објавено на ПОИМ:
6 јуни 2019 година
Начин на цитирање на статијата:
Е. Петковска, Математика во модниот дизајн, Портал ПОИМ на Институтот за математика, ПМФ, Скопје, 6 јуни 2019 год., http://poim-pmf.weebly.com/matematika-vo-modniot-dizajn.html
[1] П. Винтерс, П. Кивлин, С. Пембертон, Математика за VIII одд., Арс Ламина, Скопје, 2016
[2] П. Винтерс, П. Кивлин, С. Пембертон, Математика за IX одд., Арс Ламина, Скопје, 2016
[3] Jovan Trajkovic, Mаjstor amater, krojenje i sivanje, Prakticna knjiga, Beograd, 1984
[4] Johan C. Bertoletti, Math in the Real World, How Fashion Designers Use Math, Infobase Publishing, 2010.
[5] Fashion Designer, https://www.math.uci.edu/mathceo/Files/Career_presentations/Fashion_Designer.pdf
[6] When Fashion Meets Geometry, Molempire, Fashion, December 1, 2010
Автор:
Елена Петковска IXв одд., ООУ„Страшо Пинџур“ - Неготино
Награден експеримент со прва награда на Ноември - Месец на науката 2018 во категоријата 7-9 одд.
Професор:
Силвана Миладинова
Објавено на ПОИМ:
6 јуни 2019 година
Начин на цитирање на статијата:
Е. Петковска, Математика во модниот дизајн, Портал ПОИМ на Институтот за математика, ПМФ, Скопје, 6 јуни 2019 год., http://poim-pmf.weebly.com/matematika-vo-modniot-dizajn.html
Авторизираните статии објавени на Порталот подлежат на законска заштита. Се забранува користење на статиите без наведување на авторот или изворот.