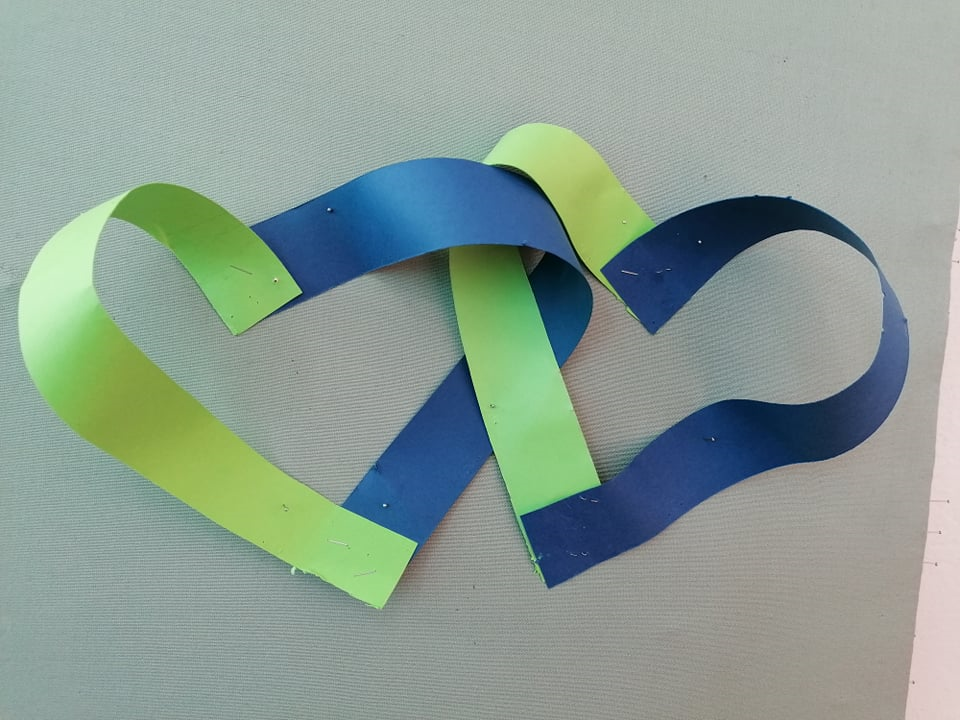|
СТАТИИ ОД МЕСЕЦОТ НА НАУКАТАСе залагаме за зголемување на свеста за местото и улогата на математиката во науките, технологијата, наставата, природата и културата.
|
|
Луда железница и чудни форми од лента
Мебиусова лента е површина со една страна и еден раб. Таа може да се добие од парче лента од хартија така што пред да се залепат краевите, на едниот од нив му правиме половина завртување. Мeбиусовата лента има една страна и еден раб. Тоа што има една страна значи дека ако ја боиме страната, целата ќе биде обоена во една боја, а доколку се движиме по нејзиниот раб ќе биде потребно двапати да „завртиме“ за да се вратиме во почетната положба и при тоа движење ќе имаме едно превртување со главата надолу и потоа уште едно со главата нагоре. Токму својството за движење на Мебиусовата лента е идејата за моделот на Мебиусовата луда железница.
Слика од моделот на Мeбиусова луда железница
Што се добива кога парче лента со завртување на едниот крај за неколку половини завртувања (за 180, 270 и 360 степени) ќе се пресече на половинки или на третинки?
1. Со залепување на краевите на лента без завртување се добива прстен (цилиндрична) површина која има две страни и два раба. Доколку неа ја пресечеме по средината, добиваме две идентични површини со исти својства како и почетната (Слика 1).
1. Со залепување на краевите на лента без завртување се добива прстен (цилиндрична) површина која има две страни и два раба. Доколку неа ја пресечеме по средината, добиваме две идентични површини со исти својства како и почетната (Слика 1).
Слика 1
2. Со залепување на краевите на лента откако на едниот му е направено половина завртување односно завртување за 180 степени, се добива површина со само една страна и еден раб – Мебиусова лента.
2.1. Доколку површината (од точка 2) ја пресечеме на средината се добива една лента двојно подолга од претходната, што значи ако се движиме по нејзиниот раб ќе поминеме растојание четири пати поголемо од должината на работ на (нај)почетната лента и притоа ќе има четири пати по половина завртување. Четирите пати по половина завртување се резултат на кружното сечење (две завртувања) и по едно половина завртување на секој од двата дела „наследени“ од почетната површина. (Слика 2.1).
2.1. Доколку површината (од точка 2) ја пресечеме на средината се добива една лента двојно подолга од претходната, што значи ако се движиме по нејзиниот раб ќе поминеме растојание четири пати поголемо од должината на работ на (нај)почетната лента и притоа ќе има четири пати по половина завртување. Четирите пати по половина завртување се резултат на кружното сечење (две завртувања) и по едно половина завртување на секој од двата дела „наследени“ од почетната површина. (Слика 2.1).
Слика 2.1 - пред
|
Слика 2.1 - потоа
|
2.2. Доколку површината (од точка 2) ја пресечеме на третина се добиваат две површини такви што едната е слична на почетната површина (по бројот на завртувања и должина), а втората е со четири пати по половина завртување и должина двојна од должината на почетната (слична на добиената лента од 2.1). (Слика 2.2).
Слика 2.2.
|
Слика 2.2.
|
3. Со залепување на краевите на лентата откако на едниот крај му се направени два пати по половина завртување (360 степени) се добива површина со две страни и два раба. Доколку се движиме по еден од нејзините рабови, по еден „круг“ ќе се вратиме од положбата од каде што сме тргнале.
3.1. Доколку површината (од точка 3) ја пресечеме на средината добиваме две идентични површини слични на почетната, кои се една во друга. (Слика 3.1)
3.1. Доколку површината (од точка 3) ја пресечеме на средината добиваме две идентични површини слични на почетната, кои се една во друга. (Слика 3.1)
Слика 3.1.
|
Слика 3.1.
|
3.2. Доколку површината (од точка 3) ја пресечеме на третини, пак се дбиваат три идентични површини слични на почетната кои се истреплетени една во друга. (Слика 3.2)
Слика 3.2.
|
Слика 3.2.
|
4. Со залепување на краевите на лентата откако на едниот крај му се направени три пати по половина завртување, односно завртување за 540 степени, се добива површина со една страна и еден раб (со слични својства како под точка 2, со тоа што разликата е во бројот на завртувања при движењето).
4.1. Доколку површината (од точка 4) ја пресечеме на средината, добиваме една лента со осум пати по половина завртувања, но лентата е во чвор. (Слика 4.1)
4.1. Доколку површината (од точка 4) ја пресечеме на средината, добиваме една лента со осум пати по половина завртувања, но лентата е во чвор. (Слика 4.1)
Слика 4.1.
|
Слика 4.1.
|
4.2. Доколку површината (од точка 3) ја пресечеме на третина, се добиваат две ленти со својства слични на лентите од точка 2.2 (разликата е во бројот на завртувања), но тие се во чвор. (Слика 4.2)
Слика 4.2.
|
Слика 4.2.
|
Што се добива кога комбинираме две ленти?
5. Комбинациите од две ленти се разликуваат од бројот на завртувања и насоката на завртување:
5.1. Комбинација од две ленти без завртувања (од вид како кај точка 1). При сечење насекоја од лентите по средина се добива квадрат. Доколку двете ленти се во различна боја тогаш паровите од спротивни страни на квадратот се во тие бои. (Слика 5.1)
5.1. Комбинација од две ленти без завртувања (од вид како кај точка 1). При сечење насекоја од лентите по средина се добива квадрат. Доколку двете ленти се во различна боја тогаш паровите од спротивни страни на квадратот се во тие бои. (Слика 5.1)
Слика 5.1.
|
Слика 5.1.
|
Слика 5.1.
5.2. Комбинација на две ленти од кои едната е без завртување (од вид како точка 1), а другата со половина завртување (од вид како кај точка 2) се добива квадрат слично како точка 5.1. (Слика 5.2)
Слика 5.2.
|
Слика 5.2.
|
Слика 5.2.
|
5.3. Комбинација од две ленти со половина завртување (од вид како кај точка 2). Резултатот зависи дали двете ленти се со завртувања во иста или спротивна насока.
5.3.1. Кога двете ленти се со завртувања во иста насока се добиваат две различни површини. (Слика 5.3.1)
5.3.1. Кога двете ленти се со завртувања во иста насока се добиваат две различни површини. (Слика 5.3.1)
Слика 5.3.1.
|
Слика 5.3.1
|
5.3.2. Кога завртувањата кај двете ленти се во спротивна насока се добива пар срца. (Слика 5.3.2)
Слика 5.3.2.
|
Слика 5.3.2
|
Користена литература:
[1] The Triz Journal, Student Corner: Mobius Strip,
https://triz-journal.com/student-corner-marvel-of-the-mobius-strip/
[2] Topology of Möbius Cuts | Simple yet Powerful Math Model for High School Students,
https://www.youtube.com/watch?v=-kA1_h1dZ58&t=94s
Автор:
Мелани Пешова VIII одд., ООУ Страшо Пинџур, Карбинци
Награден проект со втора награда на Ноември – Месец на науката 2019 во категорија 7-9 одд.
Професор:
Силвана Јакимовска Бинова
Објавено на ПОИМ:
18 март 2020 година
Начин на цитирање на статијата:
М. Пешова, Луда железница и чудни форми од лента, Портал ПОИМ на Институтот за математика, ПМФ, Скопје, 18 март 2020 год., http://poim-pmf.weebly.com/luda-zeleznica.html
[1] The Triz Journal, Student Corner: Mobius Strip,
https://triz-journal.com/student-corner-marvel-of-the-mobius-strip/
[2] Topology of Möbius Cuts | Simple yet Powerful Math Model for High School Students,
https://www.youtube.com/watch?v=-kA1_h1dZ58&t=94s
Автор:
Мелани Пешова VIII одд., ООУ Страшо Пинџур, Карбинци
Награден проект со втора награда на Ноември – Месец на науката 2019 во категорија 7-9 одд.
Професор:
Силвана Јакимовска Бинова
Објавено на ПОИМ:
18 март 2020 година
Начин на цитирање на статијата:
М. Пешова, Луда железница и чудни форми од лента, Портал ПОИМ на Институтот за математика, ПМФ, Скопје, 18 март 2020 год., http://poim-pmf.weebly.com/luda-zeleznica.html
Авторизираните статии објавени на Порталот подлежат на законска заштита. Се забранува користење на статиите без наведување на авторот или изворот.
