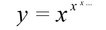НАУЧНО - ПОПУЛАРНИ СТАТИИСе залагаме за зголемување на свеста за местото и улогата на математиката во науките, технологијата, наставата, природата и културата.
|
Ламберт, Ојлер, Старите Грци и Ламбертовата функција
(Темата е презентирана и на Првиот семинар „Математика и примени“, 14 декември 2016)
(апстракт), (презентација), (ПОИМ статија), (труд)
(апстракт), (презентација), (ПОИМ статија), (труд)
Во сите науки кои ја применуваат математиката проблемите често се моделираат по принцип на повторувачка појава, односно врз база на итерација на елементарен процес. Начинот на формулирање на овие проблеми се состои во поставување на равенки или диференцијални равенки кои многу често ги вклучуваат трансцендентните експоненцијална или логаритамска функција. Познатиот број е најчесто е нивна основа. Токму Ламбертовата функција y=W(x) дефинирана имплицитно како инверзија на функцијата f(x) =x∙exp(x), дава затворен облик на решенијата на наведените проблеми во природните, општествените и инженерските науки. Интересни се историските аспекти на името, ознаката, појавата и примената на Ламбертовата функција. И покрај растењето на можностите за примена на Ламбертовата функција со развитокот на науката, технологијата и општеството, нејзиното присуство често оди непрепознаено. Овој текст е еден придонес кон нејзиното препознавање при средба со неа во образованието и во примената.
1. Како изгледа Ламбертовата функција
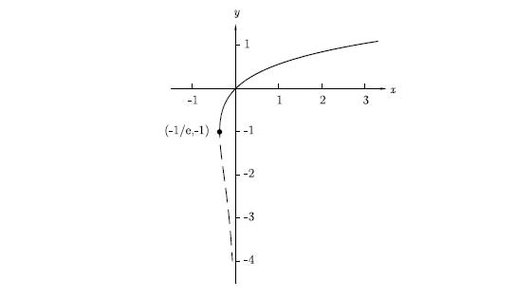
Ламбертовата функција е инверзната функција на функцијата f(x)=x∙exp(x), за x од множеството на реални броеви. Со exp(x) е означена експоненцијалната функција со основа е и експонент x. Истата дефиниција за Ламбертовата функција важи и за множеството на комплексни броеви. За означување на Ламбертовата функција ја користиме нејзината ознака W(x) и пишуваме x=W(x)∙exp(W(x)). Имплицитноста во овој запис е очигледна, но ова е дефинирачката равенка за Ламбертовата функција – таа е решение на оваа равенка. Со малку изводи, излегува дека f(x) =x∙exp(x) е немонотона функција, односно е монотона по делови и има минимум во точката (-1, -1/е). Ова значи дека Ламбертовата функција, како нејзина инверзија, не е сосема вистинска функција бидејќи е повеќевредносна. Затоа таа се дели на две функции, наречени гранки на Ламбертовата функција. Двете гранки се несиметрични, немаат ни осна, ни централна симетрија,па затоа Ламбертовата функција е згодна како прв, најлесен пример за изучување на функции со нетривијално разгранување.
1. Како изгледа Ламбертовата функција
Ламбертовата функција е инверзната функција на функцијата f(x)=x∙exp(x), за x од множеството на реални броеви. Со exp(x) е означена експоненцијалната функција со основа е и експонент x. Истата дефиниција за Ламбертовата функција важи и за множеството на комплексни броеви. За означување на Ламбертовата функција ја користиме нејзината ознака W(x) и пишуваме x=W(x)∙exp(W(x)). Имплицитноста во овој запис е очигледна, но ова е дефинирачката равенка за Ламбертовата функција – таа е решение на оваа равенка. Со малку изводи, излегува дека f(x) =x∙exp(x) е немонотона функција, односно е монотона по делови и има минимум во точката (-1, -1/е). Ова значи дека Ламбертовата функција, како нејзина инверзија, не е сосема вистинска функција бидејќи е повеќевредносна. Затоа таа се дели на две функции, наречени гранки на Ламбертовата функција. Двете гранки се несиметрични, немаат ни осна, ни централна симетрија,па затоа Ламбертовата функција е згодна како прв, најлесен пример за изучување на функции со нетривијално разгранување.
Цртеж 1. Ламбертовата функција на реалниот домен. Едната гранка е означена со испрекината линија, а другата – со полна линија. (извор: [5])
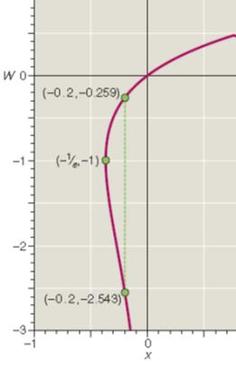
Цртеж 2. Двојна вредност на пример за x=–0.2 (извор: [4])
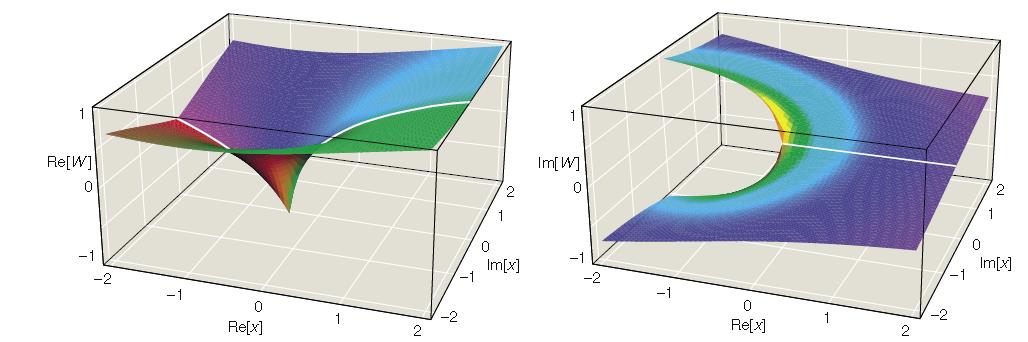
Во множеството на комлексни броеви (по домен и опсег), графичкиот приказ е тридимензионален и уште поинтересен.
Цртеж 3. Површината одлево го прикажува реалниот дел од Ламбертовата функција, а површината оддесно,
имагинарниот дел за вредности на комплексната рамнина, блиску до комплексната нула. Белата линија на
површините е проекција на реалната оска – линијата по која броевите имаат имагинарен дел 0. Шпицот на
реалната површина и прекинот кај имагинарната површина е за x=-1/е.Цртежот е од визуелизациите:
http://functions.wolfram.com/ElementaryFunctions/ProductLog2/visualizations/2/
имагинарниот дел за вредности на комплексната рамнина, блиску до комплексната нула. Белата линија на
површините е проекција на реалната оска – линијата по која броевите имаат имагинарен дел 0. Шпицот на
реалната површина и прекинот кај имагинарната површина е за x=-1/е.Цртежот е од визуелизациите:
http://functions.wolfram.com/ElementaryFunctions/ProductLog2/visualizations/2/
Гранките на реалниот домен се нарекуваат главна гранка (полната линија на црт.1.) и негативна гранка (испрекинатата линија на црт.1). Решенијата на x=W(x)∙exp(W(x)) се такви што за x≥0 има единствено решение, за –1/е ≤ x< 0 има две решенија, а за сите вредности на x<–1/е нема решение.
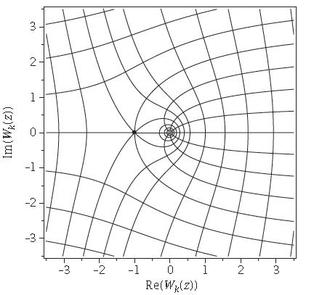
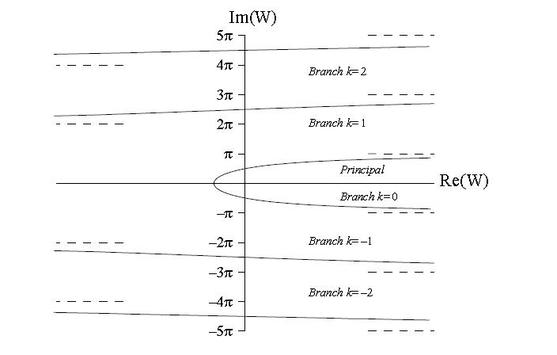
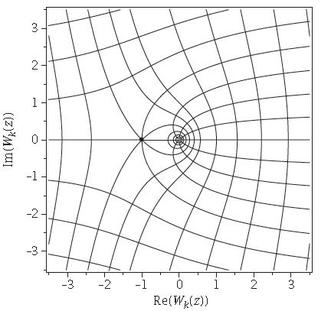
За даден комлексен број z, равенката z=W(z)∙exp(W(z)) има решенија во пребројлив број на гранки нумерирани со индекс k до W, каде што k е цел број. На следниот цртеж, за различни k и z се дадени проекциите на гранките во комплексната рамнина.
За даден комлексен број z, равенката z=W(z)∙exp(W(z)) има решенија во пребројлив број на гранки нумерирани со индекс k до W, каде што k е цел број. На следниот цртеж, за различни k и z се дадени проекциите на гранките во комплексната рамнина.
Цртеж 4. Комплексните гранки проектирани на комплексната рамнина.
Црната точка одговара на црната точка од црт.1. (извор: [3])
Црната точка одговара на црната точка од црт.1. (извор: [3])
Прашањето зошто една имплицитно дефинирана повеќевредносна функција има име и ознака е предизвикувачко, па прво ќе посветиме внимание на тоа. Всушност, Ламбертовата функција има интересна историја со интересни личности и неверојатно голема примена.
2. Кој ја открил Ламбертовата функција
Се чини дека историјата на Ламбертовата функција може да почне од Стара Грција за која знаеме дека многу го развила геометрискиот пристап. Секако, со право може да се сомневаме дека старите Грци би дошле до ваков имплицитен концепт базиран на друг ирационален број освен оној незгоден број π кој упорно им се појавувал во мерките за кругот. Но сепак, во нивната потрага за трисекција на агол и квадратура на кругот, добиле поим за првата друга крива освен кружницата. Новата крива не се конструирала само со шестар и линијар и за првпат бил искористен метод за исцртување точка по точка.
Белешките на Платон документираат за софистот Хипиас од Елис кој живеел околу 460 г. пред новата ера, помлад современик на Сократ кој, како и сите софисти, патувал по градовите и областите на Стара Грција и држел предавања, говори, бил талентиран дипломат и авторитет во правните работи, се занимавал и со уметностите (музика, поезија, сликарство, вајарство), како и со математика. Денес, нему му се припишува идејата за „природни закони“. Ученикот на Платон, геометарот Диностратус, во своите белешки го дискутира математичкиот придонес на Хипиас од Елис – пронаоѓањето на една крива за чија конструкција е потребно повеќе од шестар и линијар, со цел да трисектира агол. Таа крива денес ја запишуваме аналитички во облик x=y∙ctg(y) и знаеме дека ја сече y-оската со најблиската гранка до апсцисата кај –π/2 и π/2. Диностратус го забележал ова својство преку можноста геометриски да се измери квадратурата на кругот со помош на оваа крива, а оттаму и името на кривата – квадратрикса. Со денешните методи се констатира дека за оваа повеќевредносна функција гранките од графикот се всушност унија на сликите на реалната оска за пресликувањето од множеството на комплексните броеви во гранките на Ламбертовата функција со комплексен аргумент, без (–∞,–1), освен за k= 0, т.е. главната гранка, [1], [2]. Хоризонталните асимптоти на гранките ја сечат y-оската во целите множители на π.
2. Кој ја открил Ламбертовата функција
Се чини дека историјата на Ламбертовата функција може да почне од Стара Грција за која знаеме дека многу го развила геометрискиот пристап. Секако, со право може да се сомневаме дека старите Грци би дошле до ваков имплицитен концепт базиран на друг ирационален број освен оној незгоден број π кој упорно им се појавувал во мерките за кругот. Но сепак, во нивната потрага за трисекција на агол и квадратура на кругот, добиле поим за првата друга крива освен кружницата. Новата крива не се конструирала само со шестар и линијар и за првпат бил искористен метод за исцртување точка по точка.
Белешките на Платон документираат за софистот Хипиас од Елис кој живеел околу 460 г. пред новата ера, помлад современик на Сократ кој, како и сите софисти, патувал по градовите и областите на Стара Грција и држел предавања, говори, бил талентиран дипломат и авторитет во правните работи, се занимавал и со уметностите (музика, поезија, сликарство, вајарство), како и со математика. Денес, нему му се припишува идејата за „природни закони“. Ученикот на Платон, геометарот Диностратус, во своите белешки го дискутира математичкиот придонес на Хипиас од Елис – пронаоѓањето на една крива за чија конструкција е потребно повеќе од шестар и линијар, со цел да трисектира агол. Таа крива денес ја запишуваме аналитички во облик x=y∙ctg(y) и знаеме дека ја сече y-оската со најблиската гранка до апсцисата кај –π/2 и π/2. Диностратус го забележал ова својство преку можноста геометриски да се измери квадратурата на кругот со помош на оваа крива, а оттаму и името на кривата – квадратрикса. Со денешните методи се констатира дека за оваа повеќевредносна функција гранките од графикот се всушност унија на сликите на реалната оска за пресликувањето од множеството на комплексните броеви во гранките на Ламбертовата функција со комплексен аргумент, без (–∞,–1), освен за k= 0, т.е. главната гранка, [1], [2]. Хоризонталните асимптоти на гранките ја сечат y-оската во целите множители на π.
Цртеж 5. Кривите x=y•ctg(y) – квадратрикса односно сликите на реалната оска за пресликувањето
на комплексните броеви во гранките на комплексната Ламбертова функција. (извор: [1])
на комплексните броеви во гранките на комплексната Ламбертова функција. (извор: [1])
Откривањето на Ламбертовата функција почнува во 1758 г. кога Јохан Хајнрих Ламберт во Acta Helvetica објавил решение на степенската равенка xⁿ+ px = q во облик на ред. Интелигентноста на методот со кој Ламберт пристапил кон решавањето го заинтересирало неговиот современик, познатиот математичар Леонард Ојлер. Тој очигледно тука насетил плодно математичко тло – всушност, методот е таков што е основа за подоцнежната теорема на Лагранж за инверзија на редови докажана од Лагранж, за која пак кон крајот на 18-ти век Ханс Хајнрих Борман дал обопштување, денес познато како формула на Лагранж-Борман. Интересно е што уредниците во Acta Helvetica, според искажувањето на Ламберт во писмата до Ојлер, му скратиле еден доказ за попрост случај, а тој ги загубил белешките. Обидувајќи се да го изведе одново, стасал многу блиску до Лагранжовата теорeма за инверзија. Запишувајќи го триномот на Ламберт во поинаков облик, Ојлер дошол до решение во облик на ред кој за еден специјален случај дава решение на трaнсцендентната равенка x•lnx=v. Во тоа решение е документирано најраното појавување на редот за функцијата W.
3. Кој е Јохан Хајнрих Ламберт
Математичарите поретко слушнале за Јохан Хајнрих Ламберт (1728–1777) бидејќи неговиот придонес во науката е универзален. Дури има и анегдота дека кога кралот Фредерик II го прашал во која наука е најстручен, Ламберт нескромно, но изгледа точно, му одговорил „Во сите“. Сепак, сите негови придонеси се базирани и мотивирани од математиката. Во енциклопедиите тој се класифицира како полимат – математичар, физичар, астроном и филозоф. Подеталната биографија на Ламберт може да се прочита на http://www-history.mcs.st-andrews.ac.uk/Biographies/Lambert.html.
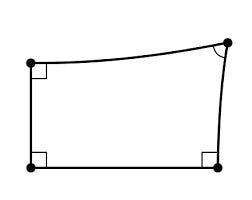
Математичкиот придонес на Ламберт во врска аксиомата на паралелност е познат во неговата студија „Теорија на паралелните линии“. Со претпоставка за исфрлање на аксиомата за паралелност, Ламберт добил голем број на неевклидско - геометриски резултати. Во негова чест четириаголникот на црт. 6 го носи неговото име.
3. Кој е Јохан Хајнрих Ламберт
Математичарите поретко слушнале за Јохан Хајнрих Ламберт (1728–1777) бидејќи неговиот придонес во науката е универзален. Дури има и анегдота дека кога кралот Фредерик II го прашал во која наука е најстручен, Ламберт нескромно, но изгледа точно, му одговорил „Во сите“. Сепак, сите негови придонеси се базирани и мотивирани од математиката. Во енциклопедиите тој се класифицира како полимат – математичар, физичар, астроном и филозоф. Подеталната биографија на Ламберт може да се прочита на http://www-history.mcs.st-andrews.ac.uk/Biographies/Lambert.html.
Математичкиот придонес на Ламберт во врска аксиомата на паралелност е познат во неговата студија „Теорија на паралелните линии“. Со претпоставка за исфрлање на аксиомата за паралелност, Ламберт добил голем број на неевклидско - геометриски резултати. Во негова чест четириаголникот на црт. 6 го носи неговото име.
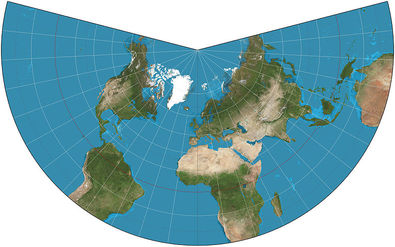
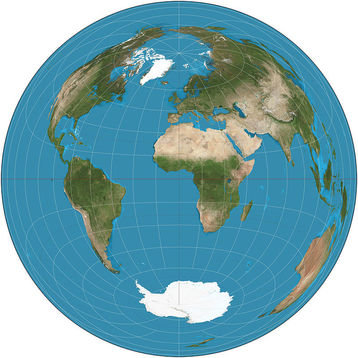
Врз основа на својата работа во денес познататите сферична и хиперболична геометрија, Ламберт изработува повеќе картографски проекции кои и денес се користат. Позната е Ламбертовата конформна конична проекција, како и Ламбертовата азимутална точно-размерна проекција. Сликите може да се видат во класичните картографски каталози, а овде ги издвојуваме:
Цртеж 8. Ламбертовата конформна конична проекција
https://en.wikipedia.org/wiki/File:Lambert_conformal_conic_projection_SW.jpg
https://en.wikipedia.org/wiki/File:Lambert_conformal_conic_projection_SW.jpg
Цртеж 9. Ламбертовата азимутална точно-размерна проекција
https://en.wikipedia.org/wiki/Lambert_azimuthal_equal-area_projection#/media/File:Lambert_azimuthal_equal-area_projection_SW.jpg
https://en.wikipedia.org/wiki/Lambert_azimuthal_equal-area_projection#/media/File:Lambert_azimuthal_equal-area_projection_SW.jpg
Во 1918 г. во специјалнотоиздание „Картографија“ како владин документ на САД, објавено е истражување за споредбата на Ламбертовата конформна конична проекција со други проекции:
https://docs.lib.noaa.gov/rescue/cgs_specpubs/QB275U35no47.pdf
Ламберт во математиката е сепак најмногу познат по доказот дека бројот π е ирационален. Дури во 2000 г. после вековната дискусија за (не)комплетноста на доказот на Ламберт (наводно, дека мора да се употреби и резултат на Лежандер), во [6] Валисер покажува дека не само што Ламбертовиот доказ е комплетен туку е и напреден за тоа време. Ламберт, изненадувачки за тоа време, поставил и хипотеза дека е и π се трансцендентни броеви, нешта кои следниот век биле докажани од Ермит (за е) и од Линдеман (за π). Валисер, пак, во својот труд го користи и заклучокот на германскиот математичар Алфред Прингшејм од 1898 г. за комплетноста и напредноста на доказот на Ламберт, кој во суштина се базира на развојот во ред на тангентната функција, а кој во тоа време не бил формално напишан. Ламберт со својот специфичен методолошки пристап кон редовите дури и покажал дека се работи за конвергентна верижна дропка.
Визионерството на Ламберт се чита и во неговите трудови меѓу 1746г. и 1748г. каде што откриваме дека Ламберт имал сон за машина за симболички пресметки! Паскаловата машина тогаш бил познат изум, но таа била само за аритметички пресметки. Сведоци сме дека неговата желба се исполнува после скоро два и пол века.
4. Ознаката W и името
Името Ламбертова функција е дадено во чест на овој научник дури во раните 80-ти години од XX век, кога во софтверскиот пакет Maple дошла потребата таа да се именува. Потребата за именување на функцијата е неслучајна. Имено, професорот Роберт Корлес од Одделот за применета математика на Универзитетот на Западен Онтарио заедно со своите соработници за Maple-овиот Computer algebra system, поминал долги часови рачно прелистувајќи книги и списанија од применетата математика во библиотеката (да се потсетиме дека тогаш електронските книги и списанија биле реткост, а интернет немало), при што откриле дека истата неименувана функција се појавува во литературата премногу пати за да се игнорира. Името lambertw за Ламбертовата функција е дадено подоцна и во пакетите Matlab, Python и Perl, а по означувањето како ProductLog во пакетот Matematica, ставен е алијас LambertW.
Ознаката W има двојно значење. Едното е дека математичарот Едвард Рајт (Sir Edward Maitland Wright, со W како прва буква на презимето) имал голем придонес за нејзината популаризација: развил систематски начин за пресметка на комплексните вредности на функцијата, пронашол нејзина примена во одредувањето на множеството решенија на даден проблем (enumeration problems), како и примена во проучувањето на стабилноста на решенијата на некои линеарни и нелинеарни диференцијални равенки. Другото значење потекнува од тоа што сè до проблемот на именување и означување во Maple, во некои трудови ја добивала често ознаката ω и дури била нарекувана Омега функција, иако денес тоа е име на друга функција. Од типографски причини, ω станува W, за што е „виновен“ професорот по информатички науки Гастон Гоне од Институтот за нумеричко програмирање (Institute for Scientific Computation) во Цирих, кој ја пишувал програмата за Ламбертовата функција во Maple.
Во 1993 г. проф. Гастон Гоне заедно со проф. Роберт Корлес во еден свој труд имале интересен коментар за Ламбертовата функција: „За една функција, добивањето на сопствено име е слично како исполнувањето на желбата на Пинокио да стане вистинско момче“.
5. Каде е потребна Ламбертовата функција
Во науката и техниката се среќаваат ситуации кои го наведуваат истражувачот математички да ги моделира со итерирано „експоненцирање“, таканаречено тетрација. Во овој вид проблеми, од важна помош во доведувањето до затворен облик на решението е токму Ламбертовата функција. Тетрацијата наречена „кула од степени“ е функцијата
https://docs.lib.noaa.gov/rescue/cgs_specpubs/QB275U35no47.pdf
Ламберт во математиката е сепак најмногу познат по доказот дека бројот π е ирационален. Дури во 2000 г. после вековната дискусија за (не)комплетноста на доказот на Ламберт (наводно, дека мора да се употреби и резултат на Лежандер), во [6] Валисер покажува дека не само што Ламбертовиот доказ е комплетен туку е и напреден за тоа време. Ламберт, изненадувачки за тоа време, поставил и хипотеза дека е и π се трансцендентни броеви, нешта кои следниот век биле докажани од Ермит (за е) и од Линдеман (за π). Валисер, пак, во својот труд го користи и заклучокот на германскиот математичар Алфред Прингшејм од 1898 г. за комплетноста и напредноста на доказот на Ламберт, кој во суштина се базира на развојот во ред на тангентната функција, а кој во тоа време не бил формално напишан. Ламберт со својот специфичен методолошки пристап кон редовите дури и покажал дека се работи за конвергентна верижна дропка.
Визионерството на Ламберт се чита и во неговите трудови меѓу 1746г. и 1748г. каде што откриваме дека Ламберт имал сон за машина за симболички пресметки! Паскаловата машина тогаш бил познат изум, но таа била само за аритметички пресметки. Сведоци сме дека неговата желба се исполнува после скоро два и пол века.
4. Ознаката W и името
Името Ламбертова функција е дадено во чест на овој научник дури во раните 80-ти години од XX век, кога во софтверскиот пакет Maple дошла потребата таа да се именува. Потребата за именување на функцијата е неслучајна. Имено, професорот Роберт Корлес од Одделот за применета математика на Универзитетот на Западен Онтарио заедно со своите соработници за Maple-овиот Computer algebra system, поминал долги часови рачно прелистувајќи книги и списанија од применетата математика во библиотеката (да се потсетиме дека тогаш електронските книги и списанија биле реткост, а интернет немало), при што откриле дека истата неименувана функција се појавува во литературата премногу пати за да се игнорира. Името lambertw за Ламбертовата функција е дадено подоцна и во пакетите Matlab, Python и Perl, а по означувањето како ProductLog во пакетот Matematica, ставен е алијас LambertW.
Ознаката W има двојно значење. Едното е дека математичарот Едвард Рајт (Sir Edward Maitland Wright, со W како прва буква на презимето) имал голем придонес за нејзината популаризација: развил систематски начин за пресметка на комплексните вредности на функцијата, пронашол нејзина примена во одредувањето на множеството решенија на даден проблем (enumeration problems), како и примена во проучувањето на стабилноста на решенијата на некои линеарни и нелинеарни диференцијални равенки. Другото значење потекнува од тоа што сè до проблемот на именување и означување во Maple, во некои трудови ја добивала често ознаката ω и дури била нарекувана Омега функција, иако денес тоа е име на друга функција. Од типографски причини, ω станува W, за што е „виновен“ професорот по информатички науки Гастон Гоне од Институтот за нумеричко програмирање (Institute for Scientific Computation) во Цирих, кој ја пишувал програмата за Ламбертовата функција во Maple.
Во 1993 г. проф. Гастон Гоне заедно со проф. Роберт Корлес во еден свој труд имале интересен коментар за Ламбертовата функција: „За една функција, добивањето на сопствено име е слично како исполнувањето на желбата на Пинокио да стане вистинско момче“.
5. Каде е потребна Ламбертовата функција
Во науката и техниката се среќаваат ситуации кои го наведуваат истражувачот математички да ги моделира со итерирано „експоненцирање“, таканаречено тетрација. Во овој вид проблеми, од важна помош во доведувањето до затворен облик на решението е токму Ламбертовата функција. Тетрацијата наречена „кула од степени“ е функцијата
и на прв поглед, изгледа дека за x > 1, вредностите за y се бесконечни. Но, се покажува дека оваа функција може да се запише во затворен облик со помош на Ламбертовата функција, а вредностите се конечни и за некои x > 1. Имено, споменатата тетрација може да се запише како итеративна низа, за која Ојлер всушност добил резултат дека конвергира за exp(–e)<x<exp(1/e) (десната страна изнесува приближно 1.445). Со неколку смени, излегува затворен облик на тетрацијата со помош на Ламбертовата функција.Тетрациите имаат примена кај фракталите. На компјутерски генерираниот фрактал на линкот во обоените региони се добиваат разни видови на конвергенција, а црните делови се сеуште недокажани во однос на видот на конвергенција:
http://www.apmaths.uwo.ca/~rcorless/frames/PAPERS/LambertW/expal2.1200.jpg
Чест пример во науките е диференцијалната равенка со аргумент на одложување (delay differential equations, DDE), [8]. Овие равенки ги проучувал Лаплас, заедно со маркизот Кондорсè (инаку попознат како „политички математичар“ заради придонесите во математичките методи на гласањето). Во своите истражувања тие имаат допирни точки со диференцијалните равенки со кои се занимавале Ојлер и Ламберт, но всушност тие допирни точки се откриле два века подоцна [12]. Во [7] е пронајден начин на преоѓање од обични кон диференцијални равеки со аргумент на одложување со помош на концептот на Ламбертовата функција.
Во физиката, Ламбертовата функција се применува во оптиката, електромагнетизмот, физиката на мали честички, општата релативност и геофизиката. Познати се Виеновиот закон за радијација на црно тело, добиен со наоѓање на максимуми на функцијата од брановите должини според Планковиот спектрален закон. Во решението фигурира Ламбертовата функција [14]. Потоа, во проблемите на кондензаторски полиња се јавуваат равенства меѓу полиномна и експоненцијална функција, типично за користење на Ламбертовата функција [11]. Исто така, таа се користи во барањето аналитичко решение на равенката на Хаисински од областа на проблемите на акцелераторите на честички, со цел да се добие лонгитудинална распределба на електроните во кружен акцелератор. Понатаму, според Шварцшилдовото решение и решението за Шварцшилдов хоризонт во општата релативност, со помош на Ламбертовата функција може да се добие закон за деформација околу масивното тело во затворен облик, [10]. Во акустиката, Ламбертовата функција има улога во фреквенциското разложување за препознавање на звук. Во квантната оптика има улога за конструкцијата на инструментот наречен Зиманов успорувач кој мора да произведе оптимално магнетно поле во методите за заробување на атоми со ласерски зрак. Ламбертовата функција се појавува и во квантно-механичкиот потенцијал.
Во електрониката, Ламбертовата функција има улога во нумеричките методи за изразување на обопштен облик на равенка за опишување на Гаусовиот шум. Исто така во електрониката е важна во моделирањето на диодно коло.
Во 3Д невровизуелизацијата (neuroimaging) Ламбертовата функција се користи во функцијата кој го поврзува мозочниот проток на крв со промените во примањето на кислород.
Во [9] е објавен метод со кој битно се олеснува постапката од имплицитна во експлицитно аналитичко решение на равенките кои ги моделираат проблемите за дефекти и критична дебелина на кристалите. Ламбертовата функција ја опишува критичната кривина на бараната дебелина на кристалите. Во проблемите од областа на хемиското инженерство, аналогно, таа се користи за определување на дебелината на стаклениот јаглерод за суперкондензатор. Во проблемите на тек на флуид низ порозен медиум, се користат двете гранки, и главната, и негативната гранка на Ламбертовата функција, зависно од стабилноста на системот.
Во биохемијата, Ламбертовата функција се користи за опишување на ензимската кинетика во временско-зависен облик, односно со примена на диференцијалните равенки со аргумент на одложување.
Благодарение на употребата на Ламбертовата функција во геофизиката [13] е најден попрецизен и експлицитен алгоритам за нелинеарен систем поврзан со проблемот на формирање на електромагнетни и диелектрични снопови во бушотините.
Во градежништвото се користат истите методи од графови (дрва) кои се користат и во информатичките науки, за пресметка на растот на пукнатини и фрактури во градбите и законот е изразен преку Ламбертовата функција.
Во хидрауличното инженерство позната е Колбруковата формула за триењето на флуид низ цевки. Со трансформација на формулата преку Ламбертовата функција и користејќи ги нумеричките методи дизајнирани за неа, пресметките стануваат попрецизни.
Листата не е исцрпена со тоа и сигурно е интересно секое ново појавување на област во науката која ја користи Ламбертовата функција.
Да се потсетиме дека не толку одамна користевме таблици за вредностите на елементарните трансцендентни функции. Сега за истите има копче на џебните дигитрони…Заради практичноста и речиси сеприсутноста на Ламбертовата функција, воопшто нема да биде чудно ако наскоро видиме и копче W(x) на дигитроните!
http://www.apmaths.uwo.ca/~rcorless/frames/PAPERS/LambertW/expal2.1200.jpg
Чест пример во науките е диференцијалната равенка со аргумент на одложување (delay differential equations, DDE), [8]. Овие равенки ги проучувал Лаплас, заедно со маркизот Кондорсè (инаку попознат како „политички математичар“ заради придонесите во математичките методи на гласањето). Во своите истражувања тие имаат допирни точки со диференцијалните равенки со кои се занимавале Ојлер и Ламберт, но всушност тие допирни точки се откриле два века подоцна [12]. Во [7] е пронајден начин на преоѓање од обични кон диференцијални равеки со аргумент на одложување со помош на концептот на Ламбертовата функција.
Во физиката, Ламбертовата функција се применува во оптиката, електромагнетизмот, физиката на мали честички, општата релативност и геофизиката. Познати се Виеновиот закон за радијација на црно тело, добиен со наоѓање на максимуми на функцијата од брановите должини според Планковиот спектрален закон. Во решението фигурира Ламбертовата функција [14]. Потоа, во проблемите на кондензаторски полиња се јавуваат равенства меѓу полиномна и експоненцијална функција, типично за користење на Ламбертовата функција [11]. Исто така, таа се користи во барањето аналитичко решение на равенката на Хаисински од областа на проблемите на акцелераторите на честички, со цел да се добие лонгитудинална распределба на електроните во кружен акцелератор. Понатаму, според Шварцшилдовото решение и решението за Шварцшилдов хоризонт во општата релативност, со помош на Ламбертовата функција може да се добие закон за деформација околу масивното тело во затворен облик, [10]. Во акустиката, Ламбертовата функција има улога во фреквенциското разложување за препознавање на звук. Во квантната оптика има улога за конструкцијата на инструментот наречен Зиманов успорувач кој мора да произведе оптимално магнетно поле во методите за заробување на атоми со ласерски зрак. Ламбертовата функција се појавува и во квантно-механичкиот потенцијал.
Во електрониката, Ламбертовата функција има улога во нумеричките методи за изразување на обопштен облик на равенка за опишување на Гаусовиот шум. Исто така во електрониката е важна во моделирањето на диодно коло.
Во 3Д невровизуелизацијата (neuroimaging) Ламбертовата функција се користи во функцијата кој го поврзува мозочниот проток на крв со промените во примањето на кислород.
Во [9] е објавен метод со кој битно се олеснува постапката од имплицитна во експлицитно аналитичко решение на равенките кои ги моделираат проблемите за дефекти и критична дебелина на кристалите. Ламбертовата функција ја опишува критичната кривина на бараната дебелина на кристалите. Во проблемите од областа на хемиското инженерство, аналогно, таа се користи за определување на дебелината на стаклениот јаглерод за суперкондензатор. Во проблемите на тек на флуид низ порозен медиум, се користат двете гранки, и главната, и негативната гранка на Ламбертовата функција, зависно од стабилноста на системот.
Во биохемијата, Ламбертовата функција се користи за опишување на ензимската кинетика во временско-зависен облик, односно со примена на диференцијалните равенки со аргумент на одложување.
Благодарение на употребата на Ламбертовата функција во геофизиката [13] е најден попрецизен и експлицитен алгоритам за нелинеарен систем поврзан со проблемот на формирање на електромагнетни и диелектрични снопови во бушотините.
Во градежништвото се користат истите методи од графови (дрва) кои се користат и во информатичките науки, за пресметка на растот на пукнатини и фрактури во градбите и законот е изразен преку Ламбертовата функција.
Во хидрауличното инженерство позната е Колбруковата формула за триењето на флуид низ цевки. Со трансформација на формулата преку Ламбертовата функција и користејќи ги нумеричките методи дизајнирани за неа, пресметките стануваат попрецизни.
Листата не е исцрпена со тоа и сигурно е интересно секое ново појавување на област во науката која ја користи Ламбертовата функција.
Да се потсетиме дека не толку одамна користевме таблици за вредностите на елементарните трансцендентни функции. Сега за истите има копче на џебните дигитрони…Заради практичноста и речиси сеприсутноста на Ламбертовата функција, воопшто нема да биде чудно ако наскоро видиме и копче W(x) на дигитроните!
Литература:
[1] R. M.Corless, G.H. Gonnet, D. E. G. Hare, D. J. Jeffrey, D. E. Knuth,On the Lambert W Function, Advances in Computational Mathematics 5 (1996) 329–359.
[2] R. M. Corless, D. J. Jeffrey, D. E. Knuth, A Sequence of Series for the Lambert W Function, ISSAC '97 Proceedings of the 1997 international symposium on Symbolic and algebraic computation, 197–204.
[3] R.M. Corless, D.J. Jeffrey, The Lambert W Function, Article III.17, The Princeton Companion to Applied Mathematics, ed. N.Higham et al,Princeton University Press, 2015.
[4] B.Hayes, Why W?, American Scientist 93 (2005) 104–109.
[5] S. Stewart, A new elementary function for our curricula?,Australian Senior Mathematics Journal 19 (2) (2005) 8–26.
[6] R Wallisser, On Lambert’s proof of the irrationality ofp, Algebraic number theory and Diophantine analysis, Graz, (1998) 521–530.
[7] F. M. Asl, A. G. Ulsoy, Analysis of a system of linear delay differential equations, Journal of Dynamic Systems, Measurement, and Control 125(2) (2003) 215–223.
[8] P. B. Brito,F. Fabiao,A. Staubyn,Euler, Lambert, and the Lambert W Function Today,The Mathematical Scientist 33 (2) (2008) 127–133.
[9] A. Braun,K.M. Briggs, P. Boni, Analytical solution to Matthews’ and Blakeslee’s critical dislocation formation thickness of epitaxially grown thin films, Journal of Crystal Growth 241 (2002) 231–234.
[10] B. Coll, A Universal Law of Gravitational Deformation for General Relativity, Relativity and Gravitation in General, Proceedings of the Spanish Relativity Meeting in Honour of the 65th Birthday of LluisBel, Salamanca, Spain, 22–25 September, 1998. Ed. J. Martín, E. Ruiz, F. Atrio, and A. Molina. World Scientific Publishers, 1999, 91–98.
[11] T. Fukushima, Precise and fast computation of Lambert W functions, without transcendental function evaluations, Journal of Computational and Applied Mathematics 244 (2013)77–89.
[12] S. R. Valluri, D. J. Jeffrey, R. M. Corless, Some Applications of the Lambert W Function to Physics, Canadian Journal of Physics 78(9) (2000) 823–831.
[13] Y. Wang, The Ricker wavelet and the LambertWfunction,Geophysical Journal International200(2015)111–115.
[14] B. W. Williams, A Specific Mathematical Form for Wien’s Displacement Law as vmax/T= constant, Journal of Chemical Education91 (2014) 623.
[1] R. M.Corless, G.H. Gonnet, D. E. G. Hare, D. J. Jeffrey, D. E. Knuth,On the Lambert W Function, Advances in Computational Mathematics 5 (1996) 329–359.
[2] R. M. Corless, D. J. Jeffrey, D. E. Knuth, A Sequence of Series for the Lambert W Function, ISSAC '97 Proceedings of the 1997 international symposium on Symbolic and algebraic computation, 197–204.
[3] R.M. Corless, D.J. Jeffrey, The Lambert W Function, Article III.17, The Princeton Companion to Applied Mathematics, ed. N.Higham et al,Princeton University Press, 2015.
[4] B.Hayes, Why W?, American Scientist 93 (2005) 104–109.
[5] S. Stewart, A new elementary function for our curricula?,Australian Senior Mathematics Journal 19 (2) (2005) 8–26.
[6] R Wallisser, On Lambert’s proof of the irrationality ofp, Algebraic number theory and Diophantine analysis, Graz, (1998) 521–530.
[7] F. M. Asl, A. G. Ulsoy, Analysis of a system of linear delay differential equations, Journal of Dynamic Systems, Measurement, and Control 125(2) (2003) 215–223.
[8] P. B. Brito,F. Fabiao,A. Staubyn,Euler, Lambert, and the Lambert W Function Today,The Mathematical Scientist 33 (2) (2008) 127–133.
[9] A. Braun,K.M. Briggs, P. Boni, Analytical solution to Matthews’ and Blakeslee’s critical dislocation formation thickness of epitaxially grown thin films, Journal of Crystal Growth 241 (2002) 231–234.
[10] B. Coll, A Universal Law of Gravitational Deformation for General Relativity, Relativity and Gravitation in General, Proceedings of the Spanish Relativity Meeting in Honour of the 65th Birthday of LluisBel, Salamanca, Spain, 22–25 September, 1998. Ed. J. Martín, E. Ruiz, F. Atrio, and A. Molina. World Scientific Publishers, 1999, 91–98.
[11] T. Fukushima, Precise and fast computation of Lambert W functions, without transcendental function evaluations, Journal of Computational and Applied Mathematics 244 (2013)77–89.
[12] S. R. Valluri, D. J. Jeffrey, R. M. Corless, Some Applications of the Lambert W Function to Physics, Canadian Journal of Physics 78(9) (2000) 823–831.
[13] Y. Wang, The Ricker wavelet and the LambertWfunction,Geophysical Journal International200(2015)111–115.
[14] B. W. Williams, A Specific Mathematical Form for Wien’s Displacement Law as vmax/T= constant, Journal of Chemical Education91 (2014) 623.
Автор:
Емилија Целакоска, Оддел за математика и информатика, Машински факултет, Скопје
Објавено на ПОИМ:
6 февруари 2017
Начин на цитирање на статијата:
Е. Целакоска, Ламберт, Ојлер, Старите грци и Ламбертовата функција, Портал ПОИМ на Институтот за математика, ПМФ, Скопје, 6 февруари 2017, http://poim-pmf.weebly.com/lambertovata-funkcija.html
Емилија Целакоска, Оддел за математика и информатика, Машински факултет, Скопје
Објавено на ПОИМ:
6 февруари 2017
Начин на цитирање на статијата:
Е. Целакоска, Ламберт, Ојлер, Старите грци и Ламбертовата функција, Портал ПОИМ на Институтот за математика, ПМФ, Скопје, 6 февруари 2017, http://poim-pmf.weebly.com/lambertovata-funkcija.html
Download (PDF)
Авторизираните статии објавени на Порталот подлежат на законска заштита. Се забранува користење на статиите без наведување на авторот или изворот.