СТАТИИ ОД МЕСЕЦОТ НА НАУКАТАСе залагаме за зголемување на свеста за местото и улогата на математиката во науките, технологијата, наставата, природата и културата.
|
Квадратна фрактална снегулка И
Квадратна фрактална површина на КоХ
|
Тела составени од правилни форми, како што се: квадрат, цилиндар, топка или конус, може да се проучуваат со примена на Евклидовата геометрија. Од друга страна голем број тела во природата, како на пример: планините, облаците, дрвјата и слично, се сложени и „неправилни“. Голем број природни тела заради својата сложеност тешко можеле да се претстават математички, сѐ до 1960 год. кога математичарот Benoit Mandelbrot пронашол начин и сложените форми да се проучуваат на систематски начин. Неговото решение се фракталите.
Што е фрактал? Фрактал е бесконечен шаблон кој е сличен на самиот себе во различни размери. Тие се создаваат со бесконечно повторување на еден едноставен процес. Фракталните облици се присутни и во човековото тело (на пр., фрактална структура имаат белите дробови, крвните садови и невроните). |
Од големиот број фрактали ние ги избравме геометриските фрактали – квадратна фрактална снегулка на Кох и квадратна фрактална површина на Кох, ги анализиравме нивните страни, плоштини и периметри во секој од чекорите на конструкција.
Модели на квадратна фрактална снегулка на Кох и квадратна фрактална површина на Кох
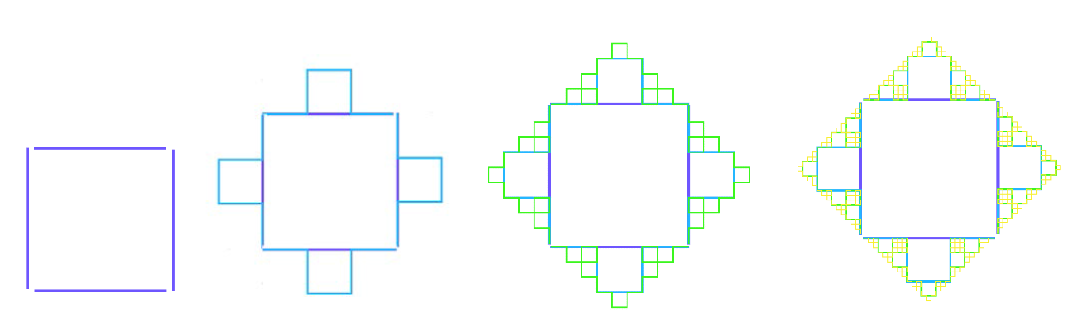
Квадратна фрактална снегулка на Кох е затворена крива слична на снегулката на Кох добиена од квадрат. Се добива со постојана замена така што во секој нареден чекор отсечките - страни на квадрат во претходен чекор, се заменуваат со линија со облик _П_, при што должината на секоја од новите отсечки во погоре дадениот облик, е 1/3 од должината на отсечката којашто е заменета (Слика 1).
Слика 1. Први четири чекори од конструкција на квадратна фрактална снегулка на Кох.
Во Табела 1 и Табела 2 се прикажани резултатите од пресметките на периметарот и плоштината на квадратна фрактална снегулка на Кох за различен чекор на замена.
Со анализа на периметарот и плоштината на фигурите, може да се покаже дека квадратна фрактална снегулка на Кох е фигура со ограничена плоштина, но со периметар кој постојано се зголемува. Снегулката на Кох има своја примена како минијатурна фрактална антена заради ограничената површина и бесконечната должина.
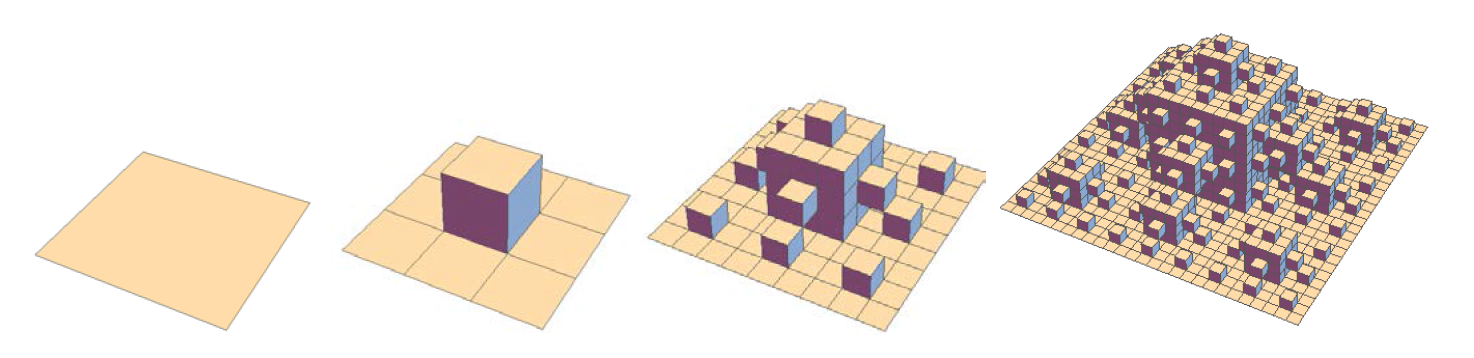
Квадратна фрактална површина на Кох е 3Д варијација на квадратна фрактална снегулка на Кох којашто започнува со квадрат, а во секој следен чекор се додава коцка над квадратот кој е во центар на секоја квадратна површина поделена на 9 квадрати (Слика 2).
Слика 2. Први четири чекори од конструкција на квадратна фрактална површина на Кох
Во следниве Табела 3 и Табела 4 се прикажани резултатите од пресметките на плоштината и волуменот на квадратна фрактална површина на Кох за различен чекор.
Може да се покаже дека квадратна фрактална површина на Кох е фигура со ограничен волумен и плоштина која се зголемува. Квадратна фрактална површина на Кох заради ограниченоста на волуменот и растечката површина е слична со белите дробови на човекот чија површина е како тениско игралиште, а волуменот од само неколку кубни дециметри. Таа има примена во индустриски процедури за кои е неопходно внимателно мешање на супстанции без користење многу енергија и без турбуленции.
Користена литература:
[1] Fractivities, Fractal Foundation, https://fractalfoundation.org/resources/fractivities/
[2] Square Koch Fractal Curves - Wolfram Demonstration Projects, https://demonstrations.wolfram.com/SquareKochFractalCurves/
[3] Square Koch Fractal Surface - Wolfram Demonstration Projects, https://demonstrations.wolfram.com/SquareKochFractalSurface/
Автор:
Христина Андонова VIII одд, ООУ Страшо Пинџур Карбинци
Проект презентиран на Ноември – Месец на науката 2019 во категоријата 7-9 одд.
Професор:
Силвана Јакимовска Бинова
Објавено на ПОИМ:
6 април 2020 година
Начин на цитирање на статијата:
Х. Андонова, Квадратна фрактална снегулка и квадратна површина на Кох, Портал ПОИМ на Институтот за математика, ПМФ, Скопје, 6 април 2020 год., http://poim-pmf.weebly.com/kvadratna-fraktalna-snegulka.html
[1] Fractivities, Fractal Foundation, https://fractalfoundation.org/resources/fractivities/
[2] Square Koch Fractal Curves - Wolfram Demonstration Projects, https://demonstrations.wolfram.com/SquareKochFractalCurves/
[3] Square Koch Fractal Surface - Wolfram Demonstration Projects, https://demonstrations.wolfram.com/SquareKochFractalSurface/
Автор:
Христина Андонова VIII одд, ООУ Страшо Пинџур Карбинци
Проект презентиран на Ноември – Месец на науката 2019 во категоријата 7-9 одд.
Професор:
Силвана Јакимовска Бинова
Објавено на ПОИМ:
6 април 2020 година
Начин на цитирање на статијата:
Х. Андонова, Квадратна фрактална снегулка и квадратна површина на Кох, Портал ПОИМ на Институтот за математика, ПМФ, Скопје, 6 април 2020 год., http://poim-pmf.weebly.com/kvadratna-fraktalna-snegulka.html
Авторизираните статии објавени на Порталот подлежат на законска заштита. Се забранува користење на статиите без наведување на авторот или изворот.