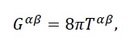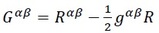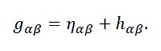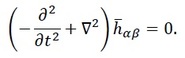НАУЧНО - ПОПУЛАРНИ СТАТИИСе залагаме за зголемување на свеста за местото и улогата на математиката во науките, технологијата, наставата, природата и културата.
|
Гравитационите бранови како потврда на Ајнштајновата теорија на релативност
(Темата е презентирана и на Работилницата „Математиката и предвидувањата“, 11 мај 2016 година)
(ПОИМ статија), (труд)
(ПОИМ статија), (труд)
Гравитационото заемнодејство е едно од четирите фундаментални заемнодејства во физиката и едно од најчудните. И покрај тоа што гравитационата сила е најстарата сила позната на човештвото, изгледа дека е најмалку разбрана. Уште од антиката, луѓето се прашувале за природата на гравитацијата, а според Аристотел, гравитацијата претставувала склоноста на телата да се движат кон нивните „природни места“. На пример водата е полесна (односно помалку густа) од земјата, па таа формира концентрична лушпа околу неа.
Најбитната теорија за гравитација со која сите сме се сретнале е Њутновата. Меѓутоа, со создавањето на Ајнштајновата специјална релативност во 1905 година, се предочиле нејзините недостатоци. Покрај непредвидувањето на абнормалната орбита на планетата Меркур (откриено преку набљудувања со транзит на Меркур пред Сонцето), според Њутн, гравитационото заемнодејство се пренесувало со бесконечна брзина.
Општата тероија на релативност е создадена од 1907 до 1915 година од Ајнштајн, а подоцна е дополнета од трудовите на други научници. Според неа, гравитацијата се заснова на идејата за простор-време претставено како четири димензионално закривено многуобразие, односно простор со одредена метрика. Преку мерењата на растојанијата, стационарни набљудувачи доаѓаат до заклучокот дека живеат на закривена површина. Овој исказ често се скратува и се вели дека гравитацијата го закривува просторот. Не само што е концептуално многу „убава“, таа опстоила на сите тестови со голем степен на прецизност.
1. Ајнштајновите равенки на поле
Овие равенки покажуваат како изворите на гравитационото поле ја определуваат метриката. Изворот на гравитационо поле во Њутновата теорија претставува густината (онаа густина на маса што ни е позната на сите). Во новата теорија, наместо густината на маса, се зема во предвид тензорот на напрегање-енергија како извор на гравитационото поле. Ова се прави со цел да се испочитува принципот на еквиваленција – не може да си дозволиме во нашата формулација да постои префериран координатен систем.
Во компонентна нотација, Ајнштајновите равенки го добиваат обликот:
Најбитната теорија за гравитација со која сите сме се сретнале е Њутновата. Меѓутоа, со создавањето на Ајнштајновата специјална релативност во 1905 година, се предочиле нејзините недостатоци. Покрај непредвидувањето на абнормалната орбита на планетата Меркур (откриено преку набљудувања со транзит на Меркур пред Сонцето), според Њутн, гравитационото заемнодејство се пренесувало со бесконечна брзина.
Општата тероија на релативност е создадена од 1907 до 1915 година од Ајнштајн, а подоцна е дополнета од трудовите на други научници. Според неа, гравитацијата се заснова на идејата за простор-време претставено како четири димензионално закривено многуобразие, односно простор со одредена метрика. Преку мерењата на растојанијата, стационарни набљудувачи доаѓаат до заклучокот дека живеат на закривена површина. Овој исказ често се скратува и се вели дека гравитацијата го закривува просторот. Не само што е концептуално многу „убава“, таа опстоила на сите тестови со голем степен на прецизност.
1. Ајнштајновите равенки на поле
Овие равенки покажуваат како изворите на гравитационото поле ја определуваат метриката. Изворот на гравитационо поле во Њутновата теорија претставува густината (онаа густина на маса што ни е позната на сите). Во новата теорија, наместо густината на маса, се зема во предвид тензорот на напрегање-енергија како извор на гравитационото поле. Ова се прави со цел да се испочитува принципот на еквиваленција – не може да си дозволиме во нашата формулација да постои префериран координатен систем.
Во компонентна нотација, Ајнштајновите равенки го добиваат обликот:
каде што
се компонентите на Ајнштајновиот тензор, кој во себе го вклучува метричкиот тензор. Со помош на метриката знаеме како да бараме растојанија помеѓу два настана, па затоа и таа игра клучна улога во теоријата.
Решавањето на Ајнштајновите равенки во нивната точна форма е многу тешка работа. Затоа, со цел да дојдеме до некои интересни физички предвидувања, ќе направиме некои поедноставувања. Бидејќи отсуството на гравитација го остава простор-времето рамно, слабо гравитационо поле ќе биде она простор-време кое е „речиси“ рамно. Ова го дефинираме како многуобразие на кое постојат координати во кои што метриката има компоненти
Решавањето на Ајнштајновите равенки во нивната точна форма е многу тешка работа. Затоа, со цел да дојдеме до некои интересни физички предвидувања, ќе направиме некои поедноставувања. Бидејќи отсуството на гравитација го остава простор-времето рамно, слабо гравитационо поле ќе биде она простор-време кое е „речиси“ рамно. Ова го дефинираме како многуобразие на кое постојат координати во кои што метриката има компоненти
Во последното равенство, првиот собирок е дијагоналната метрика на рамниот простор, наречен простор на Минковски, која што ја има следната форма: (-1, 1, 1, 1), додека вториот собирок е мала пертубација. Со помош на овие, но и некои други трансформации, ги добиваме Ајнштајновите равенки за слаби полиња:
Ова се таканаречените равенки на поле на „линеаризираната теорија“ поради тоа што се изведени задржувајќи ги членовите кои се само линеарни по пертурбацијата.
2. Гравитационо зрачење
Сега доаѓаме до делот што е најинтересен за нас, а тоа е анализата на горните равенки. Забележуваме дека тие важат за област од простор-времето каде што гравитационото поле е слабо, но не е стационарно, и тоа, се запишани за областа надвор од изворот (Т=0). Оваа ситуација се јавува далеку од изворот кој бил причинител на некои брзи промени кои се случиле одамна во времето. Но оваа равенка ја препознаваме како брановата равенка која се стретнува насекаде во физиката, а нејзиното решение е рамен бран.
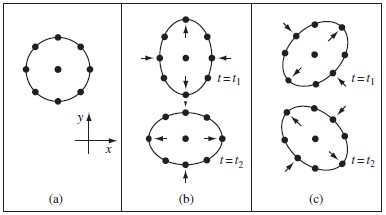
Впрочем се добива дека ако имаме две честички, ефектот на ваков бран би бил промена на сопственото растојание помеѓу нив со текот на времето (на Сликата 1 се прикажани две различни видови на гравитациони бранувања кои доаѓаат од долу и влијаат на прстенот составен од честички).
2. Гравитационо зрачење
Сега доаѓаме до делот што е најинтересен за нас, а тоа е анализата на горните равенки. Забележуваме дека тие важат за област од простор-времето каде што гравитационото поле е слабо, но не е стационарно, и тоа, се запишани за областа надвор од изворот (Т=0). Оваа ситуација се јавува далеку од изворот кој бил причинител на некои брзи промени кои се случиле одамна во времето. Но оваа равенка ја препознаваме како брановата равенка која се стретнува насекаде во физиката, а нејзиното решение е рамен бран.
Впрочем се добива дека ако имаме две честички, ефектот на ваков бран би бил промена на сопственото растојание помеѓу нив со текот на времето (на Сликата 1 се прикажани две различни видови на гравитациони бранувања кои доаѓаат од долу и влијаат на прстенот составен од честички).
Слика 1.
Дополнително, гравитационите бранови ќе создадат поголема промена во растојанието доколку почетната оддалеченост помеѓу честичките или телата била поголема. Ова е причината поради која што модерните детектори на гравитациони бранови се градат во големи размери со димензии од редот на неколку километри. Од друга страна, се заклучува дека ефектот кој што треба да се измери е релативна промена на растојанието од еден дел во отприлика 10^21.
3. Откривање на гравитационите бранови
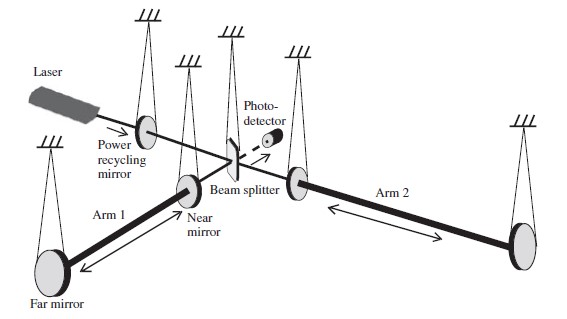
Во праксата, еден од најважните методи за мерење на ширењето и растегнувањето на просторот се состои во испраќање на фотони (ласерски зраци) помеѓу слободни честички и определување на промените во времето на патување на светлината низ двата крака на инструментот. Ова е всушност и принципот на работа на ласерскиот интерферометар како детектор на гравитациони бранови (Слика 2). Светлината од ласерот се дели со помош на делачот на зраци, па двата зрака кои што продолжуваат по должината на двата крака ќе бидат во чекор еден со друг – ако едниот отпочне со максимум, тогаш и другиот отпочнува со максималната вредност. Ако за времето на патување на зраците низ соодветните раце на интерферометарот, низ него помине гравитационен бран и едниот крак се скрати, а другиот се издолжи, тогаш ќе се појави интерференција помеѓу двата ласерски зрака кога ќе се вратат, а ова ќе биде детектирано со фотодетекторот.
3. Откривање на гравитационите бранови
Во праксата, еден од најважните методи за мерење на ширењето и растегнувањето на просторот се состои во испраќање на фотони (ласерски зраци) помеѓу слободни честички и определување на промените во времето на патување на светлината низ двата крака на инструментот. Ова е всушност и принципот на работа на ласерскиот интерферометар како детектор на гравитациони бранови (Слика 2). Светлината од ласерот се дели со помош на делачот на зраци, па двата зрака кои што продолжуваат по должината на двата крака ќе бидат во чекор еден со друг – ако едниот отпочне со максимум, тогаш и другиот отпочнува со максималната вредност. Ако за времето на патување на зраците низ соодветните раце на интерферометарот, низ него помине гравитационен бран и едниот крак се скрати, а другиот се издолжи, тогаш ќе се појави интерференција помеѓу двата ласерски зрака кога ќе се вратат, а ова ќе биде детектирано со фотодетекторот.
Слика 2.
Најголемиот детектор на Земјата со кој се пронајдени гравитационите бранови за прв пат е LIGO (Laser Interferometer Gravitational-Wave Observatory), со должина на краците од 4 километри. Со ова откритие објавено на 11-ти февруари 2016 година, всушност е даден и уште еден доказ на теоријата за општа релативност, и тоа еден век после предвидувањето на Ајнштајн во 1916 година.
4. Ширење и примена на гравитационите бранови
Најдовме дека гравитационите бранови се движат како електромагнетните бранови со брзина на еднаква на брзината на светлината. Но, покрај тоа, тие не ги делат истите карактеристики на електромагнетното зрачење. Имено, обичната материја силно влијае на светлината или електромагнетното зрачење и таа во нејзино присуство може да скршне од нејзиниот пат – можно е да се одбива, да се расејува, апсорбира итн. Спротивно на тоа, гравитационите бранови речиси и да не се засегнати од присуството на „пречки“. На овој начин, гравитационите бранови се скапоцени извори на информации за различни настани во вселената: можеме во принцип да ги користиме за да „погледнеме“ во центрите на супернови експлозии, низ облаци од меѓуѕвездена прашина или пак, по само неколку делови од секундата после Големата експлозија кога универзумот бил стар само 10^(-25) s. На пример, на електромагнетното зрачење емитирано од центарот на супернова експлозија би му било потребно доста долго време за да излезе од центарот бидејќи по патот би се расејувало безброј пати од околниот густ материјал, а освен тоа, по излегувањето би загубило и многу од информациите поради тоа.
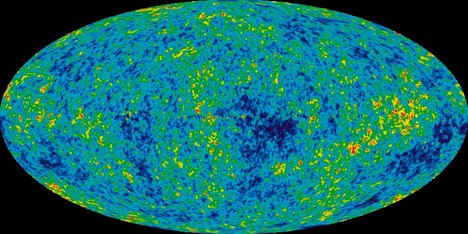
Како втор пример, на Сликата 3 се прикажани резултатите од проектот WMAP – флуктуациите на температурата на универзумот. Истражувањата покажале дека 95% од универзумот се состои од темна материја и темна енергија, дека закривеноста на просторот отстапува само 0,4% од рамен простор, како и дека универзумот „излегол“ од космичкиот темен период отприлика 400 милиони години после Големата експлозија.
4. Ширење и примена на гравитационите бранови
Најдовме дека гравитационите бранови се движат како електромагнетните бранови со брзина на еднаква на брзината на светлината. Но, покрај тоа, тие не ги делат истите карактеристики на електромагнетното зрачење. Имено, обичната материја силно влијае на светлината или електромагнетното зрачење и таа во нејзино присуство може да скршне од нејзиниот пат – можно е да се одбива, да се расејува, апсорбира итн. Спротивно на тоа, гравитационите бранови речиси и да не се засегнати од присуството на „пречки“. На овој начин, гравитационите бранови се скапоцени извори на информации за различни настани во вселената: можеме во принцип да ги користиме за да „погледнеме“ во центрите на супернови експлозии, низ облаци од меѓуѕвездена прашина или пак, по само неколку делови од секундата после Големата експлозија кога универзумот бил стар само 10^(-25) s. На пример, на електромагнетното зрачење емитирано од центарот на супернова експлозија би му било потребно доста долго време за да излезе од центарот бидејќи по патот би се расејувало безброј пати од околниот густ материјал, а освен тоа, по излегувањето би загубило и многу од информациите поради тоа.
Како втор пример, на Сликата 3 се прикажани резултатите од проектот WMAP – флуктуациите на температурата на универзумот. Истражувањата покажале дека 95% од универзумот се состои од темна материја и темна енергија, дека закривеноста на просторот отстапува само 0,4% од рамен простор, како и дека универзумот „излегол“ од космичкиот темен период отприлика 400 милиони години после Големата експлозија.
Слика 3.
За крај, далеку и од она што може да го предвидиме, можеме да бидеме речиси сигурни дека спектарот на гравитациони бранови крие многу изненадувања за нас – укажувања на феномени за коишто сеуште не сме свесни. Како што спомнавме, астрофизичарите знаат дека само 4% од масата во универзумот отпаѓа на честички кои зрачат и заемнодејствуваат со електромагнетно зрачење, додека останатите 96%, кои ги вклучуваат темната материја и темната енергија не зрачат електромагнетно, но може да зрачат гравитациони бранови. Не е изненадувачки фактот што се вложува значителен труд кон создавање на осетливи антени за гравитациони бранови.
Извори:
[1] “History of gravitational theory - Wikipedia, the free encyclopedia “. Wikimedia Foundation, Inc., 3 May 2016. Web. < https://en.wikipedia.org/wiki/History_of_gravitational_theory>.
[2] K. Sundermeyer, Symmetries in Fundamental Physics, Springer, Germany (2014).
[3] “Tests of general relativity - Wikipedia, the free encyclopedia“. Wikimedia Foundation, Inc., 23 Apr 2015. Web. < https://en.wikipedia.org/wiki/Tests_of_general_relativity>.
[4] B. Schutz, A First Course in General Relativity (Second Edition), Cambridge University Press, New York (2009).
[5] С. Т. Торнтон и Е. Рекс, Модерна физика за научници и инжинери, превод од англиски јазик: А. Тунтев, Табернакул, Скопје (2011).
Автор:
Љупчо Петров, Институт за физика, Природно математички факултет, Скопје
Објавено на ПОИМ:
12 јуни 2016
Начин на цитирање на статијата:
Љ. Петров, Гравитационите бранови како потврда на Ајншајновата теорија на релативност, Портал ПОИМ на Институтот за математика, ПМФ, Скопје, 12 јуни 2016, http://poim-pmf.weebly.com/gravitacioni-branovi.html
Download (PDF)
Авторизираните статии објавени на Порталот подлежат на законска заштита. Се забранува користење на статиите без наведување на авторот или изворот.
[1] “History of gravitational theory - Wikipedia, the free encyclopedia “. Wikimedia Foundation, Inc., 3 May 2016. Web. < https://en.wikipedia.org/wiki/History_of_gravitational_theory>.
[2] K. Sundermeyer, Symmetries in Fundamental Physics, Springer, Germany (2014).
[3] “Tests of general relativity - Wikipedia, the free encyclopedia“. Wikimedia Foundation, Inc., 23 Apr 2015. Web. < https://en.wikipedia.org/wiki/Tests_of_general_relativity>.
[4] B. Schutz, A First Course in General Relativity (Second Edition), Cambridge University Press, New York (2009).
[5] С. Т. Торнтон и Е. Рекс, Модерна физика за научници и инжинери, превод од англиски јазик: А. Тунтев, Табернакул, Скопје (2011).
Автор:
Љупчо Петров, Институт за физика, Природно математички факултет, Скопје
Објавено на ПОИМ:
12 јуни 2016
Начин на цитирање на статијата:
Љ. Петров, Гравитационите бранови како потврда на Ајншајновата теорија на релативност, Портал ПОИМ на Институтот за математика, ПМФ, Скопје, 12 јуни 2016, http://poim-pmf.weebly.com/gravitacioni-branovi.html
Download (PDF)
Авторизираните статии објавени на Порталот подлежат на законска заштита. Се забранува користење на статиите без наведување на авторот или изворот.