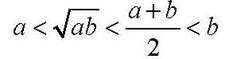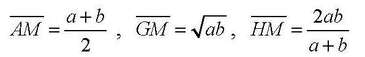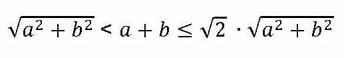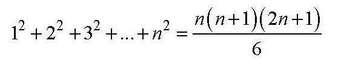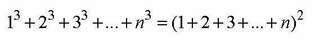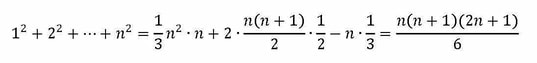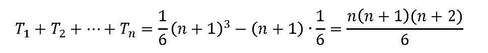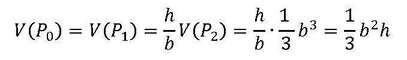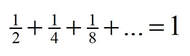СТАТИИ ОД МЕСЕЦОТ НА НАУКАТАСе залагаме за зголемување на свеста за местото и улогата на математиката во науките, технологијата, наставата, природата и културата.
|
Докази без зборови
Математичките цртежи поврзани со докази потекнуваат од антиката. Се појавиле во Кина, Арабија, Грција и Индија. Во последните децении има зголемен интерес за таканаречените „докази без зборови“. Стотици од нив се објавени во математичките списанија, во книги и на интернет.
Илустрацијата на доказите без зборови обично се прави преку претставување на броевите со графички елементи: точки, квадрати, должини на отсечки, плоштини и волумени на фигури, итеративни процедури.
Можеме ли доказот без зборови да го сметаме за вистински доказ? Во некои примери навистина се работи за многу уверлив доказ, но некаде не е така. Понекогаш со анализата на сликата е дадена само идејата и патот на формалниот доказ. Некои математичари сметаат дека доказите без зборови можат да прикажат само еден одреден случај, но не и генерализацијата на теоремата. Фактот дека визуализацијата е непотполн доказ не би требало да не спречи да ја употребуваме како средство за докажување во математиката, затоа што може да биде многу корисно и ефикасно средство во различни математички активности. А она што треба да настојуваме е постојано да бараме нови начини во докажувањето на математичките тврдења, кои можат да доведат до нови откритија.
Илустрацијата на доказите без зборови обично се прави преку претставување на броевите со графички елементи: точки, квадрати, должини на отсечки, плоштини и волумени на фигури, итеративни процедури.
Можеме ли доказот без зборови да го сметаме за вистински доказ? Во некои примери навистина се работи за многу уверлив доказ, но некаде не е така. Понекогаш со анализата на сликата е дадена само идејата и патот на формалниот доказ. Некои математичари сметаат дека доказите без зборови можат да прикажат само еден одреден случај, но не и генерализацијата на теоремата. Фактот дека визуализацијата е непотполн доказ не би требало да не спречи да ја употребуваме како средство за докажување во математиката, затоа што може да биде многу корисно и ефикасно средство во различни математички активности. А она што треба да настојуваме е постојано да бараме нови начини во докажувањето на математичките тврдења, кои можат да доведат до нови откритија.
1. Претставување на броеви со графички елементи
Во многу проблеми кои ги опфаќаат природните броеви (1, 2, ...), може да се добие увид со претставување на броевите преку множества објекти. Бидејќи изборот на објекти не е важен, вообичаено ќе користиме точки, квадрати, сфери, коцки и други обични објекти коишто лесно се цртаат.
Кога ќе се соочиме со задача за докажување на некое тврдење кое ги вклучува природните броеви (на пример, да се покаже дека збирот на првите n непарни броеви е n²) , чест приод е користењето на математичката индукција. Сепак, таквиот аналитички или алгебарски приод ретко покажува зошто тврдењето е точно. Геометрискиот приод, каде што може да се визуeлизира односот помеѓу броевите како однос помеѓу множества од точки, често може да обезбеди некое разбирање.
Во овој дел ќе илустрираме два едноставни принципи (првиот е принципот на Фубини, а вториот е принципот на Кантор), кои опфаќаат претсавување на природни броеви со множества од објекти. Тие се:
Во многу проблеми кои ги опфаќаат природните броеви (1, 2, ...), може да се добие увид со претставување на броевите преку множества објекти. Бидејќи изборот на објекти не е важен, вообичаено ќе користиме точки, квадрати, сфери, коцки и други обични објекти коишто лесно се цртаат.
Кога ќе се соочиме со задача за докажување на некое тврдење кое ги вклучува природните броеви (на пример, да се покаже дека збирот на првите n непарни броеви е n²) , чест приод е користењето на математичката индукција. Сепак, таквиот аналитички или алгебарски приод ретко покажува зошто тврдењето е точно. Геометрискиот приод, каде што може да се визуeлизира односот помеѓу броевите како однос помеѓу множества од точки, често може да обезбеди некое разбирање.
Во овој дел ќе илустрираме два едноставни принципи (првиот е принципот на Фубини, а вториот е принципот на Кантор), кои опфаќаат претсавување на природни броеви со множества од објекти. Тие се:
- Ако ги изброиш објектите во едно множество на два начина, ќе го добиеш истиот резултат (принцип на Фубини); и
- Ако постои биекција меѓу две множества, тогаш тие множества имаат ист број елементи (принцип на Кантор).
1.1. Збир на непарни броеви
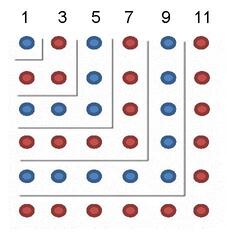
Да го утврдиме тврдњето за збирот на непарните броеви спомнати погоре, т.е. 1+3+5+ ... (2n-1) = n². Во Слика 1.1, можеме да ги изброиме точките на два начина, со множење на бројот на редици со бројот на колони (n · n), или преку бројот на точки во секој L-регион (1+3+5+ ... + (2n-1)). Според принципот на Фубини, овие две броења треба да се исти, што го потврдува доказот. Иако на Слика 1.1 само е илустриран идентитетот за случајот n = 6, шемата очигледно важи за кој било природен број n.
Да го утврдиме тврдњето за збирот на непарните броеви спомнати погоре, т.е. 1+3+5+ ... (2n-1) = n². Во Слика 1.1, можеме да ги изброиме точките на два начина, со множење на бројот на редици со бројот на колони (n · n), или преку бројот на точки во секој L-регион (1+3+5+ ... + (2n-1)). Според принципот на Фубини, овие две броења треба да се исти, што го потврдува доказот. Иако на Слика 1.1 само е илустриран идентитетот за случајот n = 6, шемата очигледно важи за кој било природен број n.
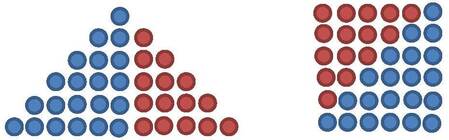
Во Слика 1.2, има две множества од точки, едното множество на десната страна е едноставо преуредување на точките на множеството на левата страна. Лесно се забележува биекцијата помеѓу елементите на двете множества (слично обоените точки се пресликуваат). Броејќи по редици во множеството на левата стана, имаме 1+3+5+ ... + (2n-1) точки, а во множеството на десната страна има n², па принципот на Кантор го утврдува резултатот.
1.2. Збир на првите n природни броеви
Можеме да ги искористиме двата принципи за да ја утврдиме класичната формула за збирот на првите n природни броеви: 1+2+3+ ... + n = n(n+1)/2. Ако придружиме колона од n точки на левата страна на низата во Слика 1.1, ќе ја добиеме низата во првата слика од Слика 1.3. Броејќи ги точките во L- регионите добиваме 2+4+ ... + 2n, додека со множење на бројот на редици со бројот на колони се добива n(n+1). Тоа значи дека принципот на Фубини го дава саканиот резултат (по делењето со 2). Алтернативно, можеме да земеме две копии од 1+2+ ... + n и да ги преуредиме точките, како во вторите две слики од Слика 1.3. Левото множеството во вторите две слики од Слика 1.3 има 2(1+ 2+ ...+ n) точки, додека десното има n² + n = n(n+1) точки. Принципот на Кантор и делењето со 2 го даваат саканиот резултат.
Можеме да ги искористиме двата принципи за да ја утврдиме класичната формула за збирот на првите n природни броеви: 1+2+3+ ... + n = n(n+1)/2. Ако придружиме колона од n точки на левата страна на низата во Слика 1.1, ќе ја добиеме низата во првата слика од Слика 1.3. Броејќи ги точките во L- регионите добиваме 2+4+ ... + 2n, додека со множење на бројот на редици со бројот на колони се добива n(n+1). Тоа значи дека принципот на Фубини го дава саканиот резултат (по делењето со 2). Алтернативно, можеме да земеме две копии од 1+2+ ... + n и да ги преуредиме точките, како во вторите две слики од Слика 1.3. Левото множеството во вторите две слики од Слика 1.3 има 2(1+ 2+ ...+ n) точки, додека десното има n² + n = n(n+1) точки. Принципот на Кантор и делењето со 2 го даваат саканиот резултат.
2. Претставување на броеви преку должини на отсечки
2.1. Неравенства на средини
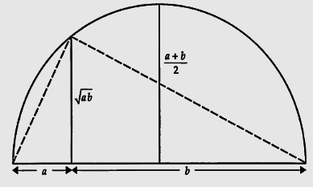
Најпознатата и најчестата средина за два броја а и b е аритметичката средина (а + b)/2, а овој број на бројната права е меѓу броевите а и b. Геометриската средина на два позитивни броеви а и b е квадратен корен од аb, која исто така на бројната права лежи меѓу броевите а и b. Кој е односот помеѓу аритметичката и геометриската средина? На Слика 2.2. a) и Слика 2.2. б) се покажува дека за 0<a<b, имаме дека:
2.1. Неравенства на средини
Најпознатата и најчестата средина за два броја а и b е аритметичката средина (а + b)/2, а овој број на бројната права е меѓу броевите а и b. Геометриската средина на два позитивни броеви а и b е квадратен корен од аb, која исто така на бројната права лежи меѓу броевите а и b. Кој е односот помеѓу аритметичката и геометриската средина? На Слика 2.2. a) и Слика 2.2. б) се покажува дека за 0<a<b, имаме дека:
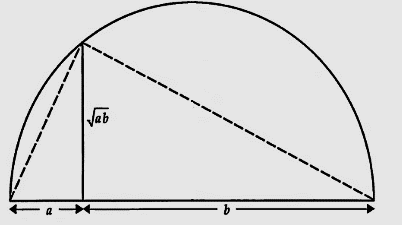
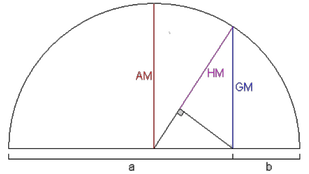
Да забележиме дека:
- триаголник кој е впишан во полукружница е правоаголен триаголник,
- висината спуштена кон хипотенузата го дели правоаголниот триаголник на помали правоаголни триаголници слични на оригиналниот, и
- односите на соодветните страни на сличните триаголници се еднакви; значи a/h= h/b, т.е. h²=аb.
Хармониската средина за два позитивни броја а и b е претставена како 2аb/(а+b) и повторно лежи помеѓу броевите а и b. Хармониската средина е помала од аритметичката и геометриската средина за 0<a<b, како што е прикажано во Слика 2.2 в). Неравенствата се резултат на споредувања на должините на страните во сличните триаголници.
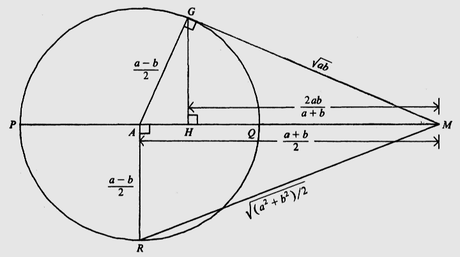
Квадратната средина за позитивните броеви а и b претставува квадратен корен од полузбирот на квадратите на броевите а и b. Таа е поголема од средините што претходно ги разгледувавме. Доказот е даден со Слика 2.3:
2.2. Неравенство на Питагора
Овде е претставен доказ со слика на едноставно двојно неравенство коешто се однесува на кои било a, b >0:
Овде е претставен доказ со слика на едноставно двојно неравенство коешто се однесува на кои било a, b >0:
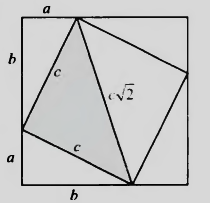
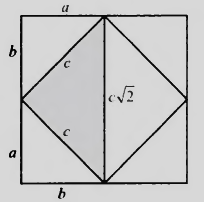
Во слика 2.4 a) ги претставуваме а и b преку катетите на правоаголниот триаголник со хипотенуза c, којашто според Питагоровата теорема е квадратен корен од збирот на квадратите на а и b. Од неравенството на триаголник, c < a+b, што го докажува првото неравентство. За доказот на второто неравенство, да забележиме дека должината на страната а + b на квадратот е помала или еднаква на должината c \/2 на дијагоналата на квадратот со страна c. Слика 2.4 б) го покажува тоа кога а = b, од каде што а+b=c \/2.
3. Претставување на броеви преку плоштини на рамнински фигури
3.1. Збир на првите n квадратни броеви
3.1. Збир на првите n квадратни броеви
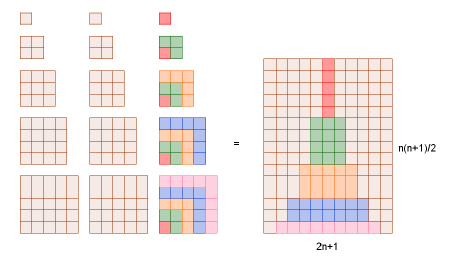
Претставувањето на идентитетот
е добиено преку покажување дека 3(1+4+9+...+n²) е еднакво по плоштина со правоаголникот со димензии 2n+1 на n(n+1)/2 (Слика 3.1).
3.2. Збир на првите n кубови од природни броеви
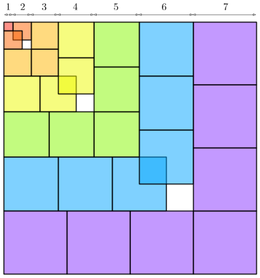
Со користење на плоштини може да го илустрираме идентитетот
Со користење на плоштини може да го илустрираме идентитетот
со претставување на куб n³ како n копии на n², за некој цел број n. Слика 3.2 го илустрира горниот идентитет. На сликата каде што два квадрати се преклопуваат во помал квадрат, секогаш има соседен празен квадрат со истата плоштина.
4. Претставување на броеви преку волумени на тела
Овде ќе претставиме позитивен број преку волумен на тело. Наједноставно, можеме да го претставиме производот на три позитивни броеви преку волуменот на квадар. Исто така можеме да претставиме број како колекција на коцки и да воспоставиме иденитети преку пресметка на волумени. Во многу случаи треба да се променат или преуредат деловите на некое тело пред да се пресмета волуменот.
Овде ќе претставиме позитивен број преку волумен на тело. Наједноставно, можеме да го претставиме производот на три позитивни броеви преку волуменот на квадар. Исто така можеме да претставиме број како колекција на коцки и да воспоставиме иденитети преку пресметка на волумени. Во многу случаи треба да се променат или преуредат деловите на некое тело пред да се пресмета волуменот.
4.1. Збир на првите n квадратни броеви
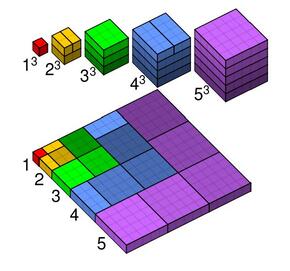
Можеме да претставиме квадрат на природен број k како колекција од k² единични коцки и да го пресметаме збирот од квадратите на следниот начин:
Можеме да претставиме квадрат на природен број k како колекција од k² единични коцки и да го пресметаме збирот од квадратите на следниот начин:
Во пресметувањето се употребува формулата за волумен на пирамида (1/3 по плоштината на основата (којашто е квадрат) по висината) и тоа дека збирот 1+2+…+n е еднаков на n(n+1)/2 (Слика 4.1).
4.2. Збир на триаголни броеви
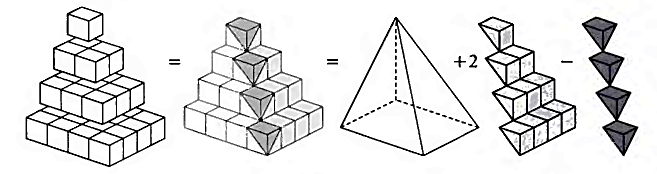
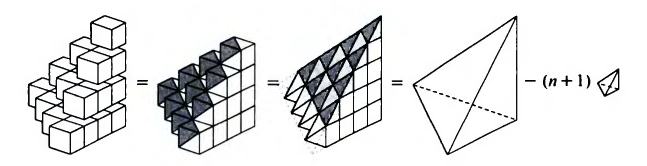
По редење на неколку единични коцки кои ги претставуваат триаголните броеви 1,3, 6, 10, 15,... (n-тиот триаголен број е еднаков на збирот на првите n природни броеви т.е. Тn=1+2+...+n), ги отстрануваме малите пирамиди (исенчени на Слика 4.2) и ја поставуваме секоја на врвот на коцката од која е отсечена. Добиваме една голема пирамида минус неколку помали пирамиди по работ на основата:
По редење на неколку единични коцки кои ги претставуваат триаголните броеви 1,3, 6, 10, 15,... (n-тиот триаголен број е еднаков на збирот на првите n природни броеви т.е. Тn=1+2+...+n), ги отстрануваме малите пирамиди (исенчени на Слика 4.2) и ја поставуваме секоја на врвот на коцката од која е отсечена. Добиваме една голема пирамида минус неколку помали пирамиди по работ на основата:
4.3. Волумен на квадратна пирамида
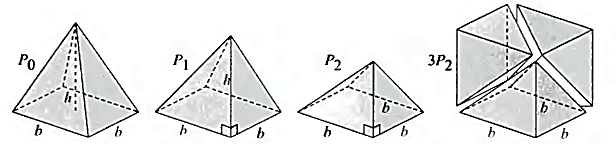
Ако Р0 е пирамида со основа квадрат со страна b и висина h, како што е илустрирано на Слика 4.3, тогаш според принципот на Кавалиери, Р0 има ист волумен како пирамидата Р1, каде што два од триаголните ѕидови се нормални на основата. Пирамидата Р2 ги има истите својства како пирамидата Р1, но нејзината висина е со должина b. Три копии од Р2 формираат коцка со страна b. Имаме:
Ако Р0 е пирамида со основа квадрат со страна b и висина h, како што е илустрирано на Слика 4.3, тогаш според принципот на Кавалиери, Р0 има ист волумен како пирамидата Р1, каде што два од триаголните ѕидови се нормални на основата. Пирамидата Р2 ги има истите својства како пирамидата Р1, но нејзината висина е со должина b. Три копии од Р2 формираат коцка со страна b. Имаме:
5. Итеративни процедури
Во блиска врска со употребата на неколку копии од слики е и следната процедура кадешто се користат копии од слики, но на начин што делот од сликата е намалена верзија од целосната слика. Ако должината на страна на најголемиот квадрат е 1 и ако ги означиме внатрешните правоаголници и квадрати со нивните соодветни плоштини, ќе добиеме визуелен доказ на сумата на геометрискиот ред со количник 1/2:
Во блиска врска со употребата на неколку копии од слики е и следната процедура кадешто се користат копии од слики, но на начин што делот од сликата е намалена верзија од целосната слика. Ако должината на страна на најголемиот квадрат е 1 и ако ги означиме внатрешните правоаголници и квадрати со нивните соодветни плоштини, ќе добиеме визуелен доказ на сумата на геометрискиот ред со количник 1/2:
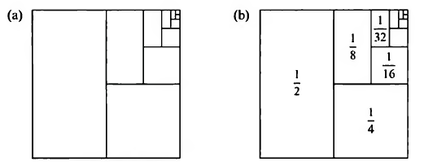
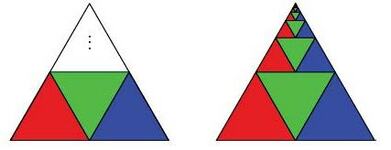
Подолу се дадени две слики кои го илустрираат редот 1/4+(1/4)²+(1/4)³+...=1/3. На првата слика забележуваме дека синиот триаголник е 1/4 од оригиналниот триаголник, следниот син триаголник е 1/4 од претходниот, итн., a заедно збирот на триаголниците изнесува 1/3 од оригиналниот триаголник (гледај една боја). Но, може да се постапи и поинаку, на пример, како на Слика 5.3.
Користена литература:
[1] R. B. Nelsen, Proofs Without Words Exercises in Visual Thinking, The Mathematical Association of America, 1993. [2] R. B. Nelsen, Proofs Without Words III Further Exercises in Visual Thinking, Lewis & Clark College, Published and Distributed by The Mathematical Association of America, 2015.
[3] MAA Publications, Proofs Without Words and Beyond,
https://www.maa.org/press/periodicals/convergence/proofs-without-words-and-beyond
Автор:
Верица Спасковска II-A год., ПСУ Јахја Кемал, Струмица
Награден експеримент со втора награда на Ноември - Месец на науката 2018 во категоријата I-IV год.
Професор:
Хатиџе Чобан
Објавено на ПОИМ:
9 јуни 2019 година
Начин на цитирање на статијата:
В. Спасковска, Докази без зборови, Портал ПОИМ на Институтот за математика, ПМФ, Скопје, 9 јуни 2019 год., http://poim-pmf.weebly.com/dokazi-bez-zborovi.html
Авторизираните статии објавени на Порталот подлежат на законска заштита. Се забранува користење на статиите без наведување на авторот или изворот.