|
СТАТИИ ОД МЕСЕЦОТ НА НАУКАТАСе залагаме за зголемување на свеста за местото и улогата на математиката во науките, технологијата, наставата, природата и културата.
|
|
буквите во математичките задачи и формули
Математиката е дел од нашето секојдневие, а бројките и буквите се основата на нашето образование. Кога ми дојде оваа идеја, прво се запрашав како би можела да соединам два сосема спротивни поими (поради тоа што прва асоцијација за буквите се јазиците, а за бројките математиката).
Главна компонента во математиката се броевите. Тие се распределени во множества кои се означуваат со следните латинични букви: N, Z, Q, I, R.
МНОЖЕСТВА
N – Множеството на природните броеви, во кое спаѓаат 1,2,3,4, итн. Ова е најмало од сите множества.
Z – Множеството на целите броеви во кое спаѓаат нулата, природните броеви и нивните спротивни, кои се нарекуваат негативни цели броеви.
Q – Множеството на рационалните броеви. Во ова множество спаѓаат сите дропки p/q , каде што p и q се цели броеви и q e различен од 0. Бидејќи q може да биде и 1 следува дека во множеството на рационалните броеви спаѓаат и целите броеви.
I – Множеството на ирационалните броеви. Во ова множество спаѓаат сите бесконечни непериодични децимални броеви како што се, на пример, броевите: π , √2, √5, -√2, -√5 итн.
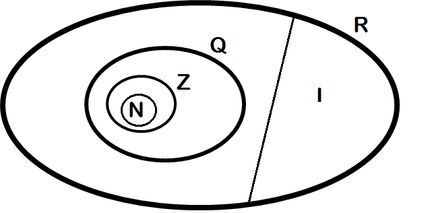
R – Множеството на реалните броеви. Ова множество претставува унија од множеството на рационалните и од множеството ирационалните броеви (прикажано на Веновиот дијаграм подолу).
Главна компонента во математиката се броевите. Тие се распределени во множества кои се означуваат со следните латинични букви: N, Z, Q, I, R.
МНОЖЕСТВА
N – Множеството на природните броеви, во кое спаѓаат 1,2,3,4, итн. Ова е најмало од сите множества.
Z – Множеството на целите броеви во кое спаѓаат нулата, природните броеви и нивните спротивни, кои се нарекуваат негативни цели броеви.
Q – Множеството на рационалните броеви. Во ова множество спаѓаат сите дропки p/q , каде што p и q се цели броеви и q e различен од 0. Бидејќи q може да биде и 1 следува дека во множеството на рационалните броеви спаѓаат и целите броеви.
I – Множеството на ирационалните броеви. Во ова множество спаѓаат сите бесконечни непериодични децимални броеви како што се, на пример, броевите: π , √2, √5, -√2, -√5 итн.
R – Множеството на реалните броеви. Ова множество претставува унија од множеството на рационалните и од множеството ирационалните броеви (прикажано на Веновиот дијаграм подолу).
|
|
|
|
|
Венов дијаграм кој ја покажува врската меѓу множествата N, Z, Q, I и R
ГЕОМЕТРИЈА
|
1. Бројот ПИ (π)
Пи (π), Лудолфов број или Арихмедова константа е ирационален реален број, кој го претставува односот на обиколката на круг и неговиот дијаметар. Бројот π има широка употреба во математиката, физиката и инженерството, но се употребува и во други науки. Бројот π исто така е познат како Арихмедова константа (што не е исто со Арихмедов број) и како Лудолфов број (по геманскиот математичар Лудолф ван Цојлен кој го пресметал π на многу децимали). |
Постојат различни начини за изразување на π како дропка, а еден од нив е претствавување во вид 22/7. Приближната вредност на π на пет децимали изнесува 3,14159. Тој, во математичките задачи, се пресметува заокружен на неговата најмала вредност: 3,14. Денови на бројот ПИ се 14 март (датумот се чита како што го читаат Американците, прво месецот, а потоа денот), односно 22 јули, поради дропката 22/7 (овој датум се чита како што го читаме ние, прво денот, а потоа месецот).
|
2. Агли
Во геометријата, покрај грчката буква π, се употребуваат и други грчки букви како ознаки за агли (α, β, γ, δ, φ, ϑ). На пример, забирот на аглите во еден триаголник е 180°, а тоа го запишуваме како α+β+γ=180°. |
|
3. Плоштина, периметар и волумен
Периметарот, плоштината и волуменот се основните пресметки што ги правиме за една геометриска фигура. Тие се бележат со буквите:
|
ПЕРИМЕТАР, ПЛОШТИНА,
ВОЛУМЕН
|
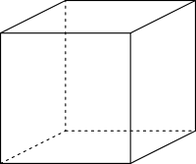
Тие букви претставуваат одредени броеви. Секоја буква има одредено значење. На пример, да ги разгледаме формулите за периметар и плоштината на квадрат, и плоштина и волумен на коцка. Со а да ја означиме должината на страната на квадратот, а со b должината на страната на коцката (прикажани на цртежот подолу). Тогаш:
- Формулата за периметар на квадрат е: L = a+a+a+a=4а
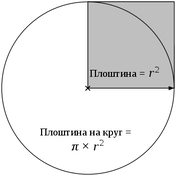
- Формулата за плоштина на квадрат е: P = a×a
- Формулата за плоштина на коцка е: P= 6×b×b
- Формулата за волумен на коцка е: V = b×b×b
|
|
АЛГЕБРА
Алгебрата е важна гранка во математиката. Таа постои од многу одамна, но со текот на времето сѐ повеќе и повеќе се усовршува. Елементарната алгебра ги изучува математичките симболи и правила за манипулирање со овие симболи. Тие симболи (кои денес се пишуваат со букви од латиницата или со грчки букви) претставуваат величини без фиксни вредности, кои се нарекуваат променливи или непознати. (Такви се а и b од претходниот пример). Променливите во математиката обично се означуваат со буквите од латиницата, x, y, z итн.
Примери. x + 2 е алгебарски израз (наречен бином), x + 2 = 5 е линеарна равенка со една непозната (тоа е x). Подолу на сликата (лево) е прикажан систем равенки со три непознати, а на сликата десно - формулата што е решение на квадратна равенка со коефициенти а, b, c.
|
|
МАТЕМАТИЧКА ЛОГИКА
Во математичката логика се употребуваат неколку важни симболи, коишто се означуваат со букви.
Тоа се T (што значи точно) и ⊥ (што значи неточно). Некаде, наместо обратно завртениот симбол Т (за неточно), се користи буквата F. Покрај овие букви, се среќаваат и буквите: обратно завртено А, т.е. ∀ (што значи „за секој“) и обратно завртено Е, т.е. ∃ (што значи „за некој“).
Тоа се T (што значи точно) и ⊥ (што значи неточно). Некаде, наместо обратно завртениот симбол Т (за неточно), се користи буквата F. Покрај овие букви, се среќаваат и буквите: обратно завртено А, т.е. ∀ (што значи „за секој“) и обратно завртено Е, т.е. ∃ (што значи „за некој“).
Користена литература:
[1] Ј. Стефановски, Н. Целакоски, Д. Ачовски, Ж. Мадевски, Г. Шопкоски, А. Алексова, Математика за седмо одделение, Алби, 2002.
[2] Ж. Мадевски, Н. Целакоски, Р. Ансаров, Геометрија со збирка задачи за VIII одделение, Просветно дело, 1996.
[3] Ј. Стефановски, Д. Ачовски, Алгенба за VIII одделение, Просветно дело, 1990.
Автор:
Ивана Иванова VII одд., ООУ „ Страшо Пинџур“- Неготино
Проект презентиран на Ноември – Месец на науката 2019 во категоријата 7-9 одд.
Професор:
Катерина Јаневска
Објавено на ПОИМ:
04 февруари 2020 година
Начин на цитирање на статијата:
И. Иванова, Буквите во математичките задачи и формули, Портал ПОИМ на Институтот за математика, ПМФ, Скопје, 04 февруари 2020 год., http://poim-pmf.weebly.com/bukvite-vo-matematikata.html
[1] Ј. Стефановски, Н. Целакоски, Д. Ачовски, Ж. Мадевски, Г. Шопкоски, А. Алексова, Математика за седмо одделение, Алби, 2002.
[2] Ж. Мадевски, Н. Целакоски, Р. Ансаров, Геометрија со збирка задачи за VIII одделение, Просветно дело, 1996.
[3] Ј. Стефановски, Д. Ачовски, Алгенба за VIII одделение, Просветно дело, 1990.
Автор:
Ивана Иванова VII одд., ООУ „ Страшо Пинџур“- Неготино
Проект презентиран на Ноември – Месец на науката 2019 во категоријата 7-9 одд.
Професор:
Катерина Јаневска
Објавено на ПОИМ:
04 февруари 2020 година
Начин на цитирање на статијата:
И. Иванова, Буквите во математичките задачи и формули, Портал ПОИМ на Институтот за математика, ПМФ, Скопје, 04 февруари 2020 год., http://poim-pmf.weebly.com/bukvite-vo-matematikata.html
Авторизираните статии објавени на Порталот подлежат на законска заштита. Се забранува користење на статиите без наведување на авторот или изворот.
