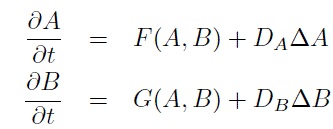НАУЧНО - ПОПУЛАРНИ СТАТИИСе залагаме за зголемување на свеста за местото и улогата на математиката во науките, технологијата, наставата, природата и културата.
|
Зошто тигрите имаат линии?
|
Секој повеќеклеточен организам го започнува животот од една клетка која наизглед има проста структура и не поседува никаква шара. Но, сепак таа се развива во многу покомплициран организам кој понекогаш се одликува со сложени облици и шари. Одговорот за оваа појава, наречена морфогенеза, го има понудено британскиот математичар Алан Тјуринг уште во 1952 година. Тјуринговата теорија за тоа како се формираат шарите кај организмите, како на пример линиите кај тигрите или точките кај леопардите, која е строго математички основана, експериментално е потврдена дури после 60 години.
|
Познато е дека последните години од својот краток живот, Тјуринг ги има посветено на работа во полето наматематичката биологија. Во 1952 година, тој го објавува својот труд The chemical basis of morphogenesis, во кој ја изложува својата теорија за формирање на шарите кај живите организми. Како што вели тој самиот, за целосно разбирање на неговата теорија потребни се добри знаења од математиката, малку биологија и малку елементарна хемија
Alan Turing (1912-1954)
Според Тјуринговата теорија, шарите кај организмите се генерирани од пар од морфогени, супстанции А и B кои земно делуваат како „активатор“ и „инхибитор“ (A ја зголемува продукцијата на B, но B ја намалува продукцијата на A). Овие супстанции реагираат (се соединуваат и формираат нови соединенија) и дифузираат (од средина со поголема, кон средина со помала концентрација) и притоа стабилната состојба на овој систем претставува хетерогена просторна шара од нивните концентрации.
Начинот на кој овие хемикалии заемно делуваат (на ниво на една клетка) може да се измоделира со помош на системот равенки на реакција и дифузија со кои се дефинира брзината на промена на концентрациите на супстанците A и B, односно
Начинот на кој овие хемикалии заемно делуваат (на ниво на една клетка) може да се измоделира со помош на системот равенки на реакција и дифузија со кои се дефинира брзината на промена на концентрациите на супстанците A и B, односно
каде што A=A(x,t) и B=B(x,t) се густините, концентрациите на супстанциите A и B, соодветно, на позицијата x во временскиот момент t, Delta е Лапласовиот оператор и DA и DB се коефициентите на дифузија на А и B, соодветно. Функциите F и G обично се нелинеарни функции и ја претставуваат компонентата на реакција која покажува како се менува концентрацијата на секоја од хемикалиите врз основа на сегашната состојба.
Математичкиот модел на системот равенки на реакција и дифузија не е најглавниот придонес на Тјуринг. Имено, тој забележал и дека нестабилноста на системот равенки е индуцирана од присуството на дифузија, но исто така тој ги окарактеризирал решенијата на системот, и најважно, ги поврзал овие решенија со одредени биолошки појави. Така, периодичните решенија над линеарна област (како на пример кожата на змијата) продуцираат шара составена од линии. Истите решенија, но над поправоаголни области може да продуцираат исто така шара со линии, но може да има и присуство на точки. Имено, со менување на параметрите во системот равенки на реакција и дифузија се добиваат најразлични шари (види Generating Textures on Arbitrary Surfaces Using Reaction-Diffusion).
Математичкиот модел на системот равенки на реакција и дифузија не е најглавниот придонес на Тјуринг. Имено, тој забележал и дека нестабилноста на системот равенки е индуцирана од присуството на дифузија, но исто така тој ги окарактеризирал решенијата на системот, и најважно, ги поврзал овие решенија со одредени биолошки појави. Така, периодичните решенија над линеарна област (како на пример кожата на змијата) продуцираат шара составена од линии. Истите решенија, но над поправоаголни области може да продуцираат исто така шара со линии, но може да има и присуство на точки. Имено, со менување на параметрите во системот равенки на реакција и дифузија се добиваат најразлични шари (види Generating Textures on Arbitrary Surfaces Using Reaction-Diffusion).
Строго математички базираната Тјурингова теорија за формирање на шарите кај организмите, 60 години била третирана како спекулативна теорија, се' до нејзината експериментална потврда во 2012 година од страна на биолозите од Кралскиот колеџ (King's Coledge) од Лондон. Овие истражувачи ги идетификувале специфичните морфогени одговорни за креирањето на шарите - FGF (Fibroblast Growth Factor) и Shh (Sonic Hedgehog). Со експерименти изведени над ембриони на глувци, тие покажале дека кога активноста на овие морфогени се зголемува или намалува, се појавуваат шари на непцето во устата на глувците, на истиот начин на кој тие се генерираат со помош на Тјуринговите равенки.
Оваа експериментална потврда, не само што и' дава признание на Тјуринговата теорија, туку овозможува во иднина морфогените да се користат во регенеративната медицина за обновување на структурата на ткивата од само една матична (стем) клетка. Познавањето на математичкиот модел на биолошката појава, овозможува посакуваните резултати да може да се симулираат пред да станат реалност и притоа да се направи правилниот избор на параметри.
Извори:
[1] A. M. Turing, The Chemical Basis of Morphogenesis, Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences, Vol. 237, No. 641. (Aug. 14, 1952), pp. 37-72
[2] Bjarni V. Halldórsson, Why do tigers have stripes? Turing’s work on mathematical biology
[3] Alan Turing's 1950s tiger stripe theory proved
[4] Christina Kuttler, Reaction-Diffusion equations with applications
[5] Avner Friedman, What Is Mathematical Biology and How Useful Is It?, Notices of the AMS, August 2010, pp.851-857
[6] Greg Turk, Generating Textures on Arbitrary Surfaces Using Reaction-Diffusion
[7] S. BARRY COOPER, JAN VAN LEEUWEN, Alan Turing HIS WORK AND IMPACT, Elsevier, 2013
Автор:
Ирена Стојковска, Институт за математика, Природно-математички факултет, Скопје
Објавено на ПОИМ:
2 јули 2015
Начин на цитирање на статијата:
И. Стојковска, Зошто тигрите имаат линии?, Портал ПОИМ на Институтот за математика, ПМФ, Скопје, 2 јули 2015, http://poim-pmf.weebly.com/zosto-tigrite-imaat-linii.html
Оваа експериментална потврда, не само што и' дава признание на Тјуринговата теорија, туку овозможува во иднина морфогените да се користат во регенеративната медицина за обновување на структурата на ткивата од само една матична (стем) клетка. Познавањето на математичкиот модел на биолошката појава, овозможува посакуваните резултати да може да се симулираат пред да станат реалност и притоа да се направи правилниот избор на параметри.
Извори:
[1] A. M. Turing, The Chemical Basis of Morphogenesis, Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences, Vol. 237, No. 641. (Aug. 14, 1952), pp. 37-72
[2] Bjarni V. Halldórsson, Why do tigers have stripes? Turing’s work on mathematical biology
[3] Alan Turing's 1950s tiger stripe theory proved
[4] Christina Kuttler, Reaction-Diffusion equations with applications
[5] Avner Friedman, What Is Mathematical Biology and How Useful Is It?, Notices of the AMS, August 2010, pp.851-857
[6] Greg Turk, Generating Textures on Arbitrary Surfaces Using Reaction-Diffusion
[7] S. BARRY COOPER, JAN VAN LEEUWEN, Alan Turing HIS WORK AND IMPACT, Elsevier, 2013
Автор:
Ирена Стојковска, Институт за математика, Природно-математички факултет, Скопје
Објавено на ПОИМ:
2 јули 2015
Начин на цитирање на статијата:
И. Стојковска, Зошто тигрите имаат линии?, Портал ПОИМ на Институтот за математика, ПМФ, Скопје, 2 јули 2015, http://poim-pmf.weebly.com/zosto-tigrite-imaat-linii.html
Download (PDF)
Авторизираните статии објавени на Порталот подлежат на законска заштита. Се забранува користење на статиите без наведување на авторот или изворот.