СТАТИИ ЗА НАСТАВАТА ПО МАТЕМАТИКАСе залагаме за зголемување на свеста за местото и улогата на математиката во науките, технологијата, наставата, природата и културата.
|
Танграми: Поглед кон математиката на еден креативен начин
|
Танграмите се еден вид сложувалки, од типот на дисекции, односно фигура исечена на делчиња, а потоа од делчињата со преместување се формира нова фигура. Во случајот на танграмите, почетната фигура е квадрат, со точно одреден начин на на кој треба да се исечат делчињата. Танграмите се одличен избор за проучување на својствата на геoметриските фигури и соодносот меѓу различни фигури по вид и големина.
Се верува дека танграмите ги создале во Кина (во време на владеењето на династијата Сонг 960-1279 год.). Во Европа, тие се донесени на почетокот од 19-тиот век. Набрзо тие стекнале светска популарност, која и до ден денес се одржува. Иако тие главно служеле за забава, се смета дека танграмите се „најстариот психолошки тест на светот“. Денес, употребата на тангамите е многу поширока. Танграмите поседуваат едукативна вредност и може да се користат во наставата по математика. |
1. Како да се направат делчињата на танграмот?
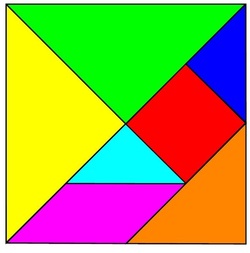
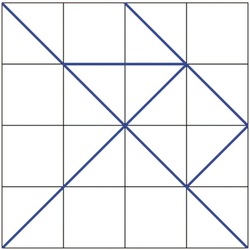
За да ги направите сами танграмските делчиња, најнапред исечете еден квадрат (од подебел картон). Големината на страната на квадратот е по желба, на пример може да биде 12cm долга. Обележете го квадратот како на дадената слика и исечете го по должината на сините линии. Така ќе добиете 7 делчиња на танграмот: 2 големи триаголници, 1 среден триаголник, 2 мали триаголници, 1 квадрат и 1 паралелограм.
За да ги направите сами танграмските делчиња, најнапред исечете еден квадрат (од подебел картон). Големината на страната на квадратот е по желба, на пример може да биде 12cm долга. Обележете го квадратот како на дадената слика и исечете го по должината на сините линии. Така ќе добиете 7 делчиња на танграмот: 2 големи триаголници, 1 среден триаголник, 2 мали триаголници, 1 квадрат и 1 паралелограм.
Слика 1. Мрежа за изработка на делчињата на танграмот
2. Составување фугури од тангамот
Основно и едниствено правило при составувањето на фигури од делчињата на танграмот е
Основно и едниствено правило при составувањето на фигури од делчињата на танграмот е
ТРЕБА ДА СЕ ИСКОРИСТАТ СИТЕ 7 ДЕЛЧИЊА И ПРИ ТОА
НЕ Е ДОЗВОЛЕНО ПРЕКЛОПУВАЊЕ НА ДЕЛЧИЊАТА.
НЕ Е ДОЗВОЛЕНО ПРЕКЛОПУВАЊЕ НА ДЕЛЧИЊАТА.
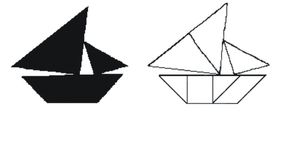
Типична танграмска сложувалка се состои од тоа што се задава исполнета или контурна слика на фигурата која треба да се состави од 7-те делчиња на танграмот. Пример на една танграмска сложувалка, за дадена исполнета слика (лево) и нејзиното решение (десно):
Слика 2. Танграмска сложувалка: исполнета слика (лево) и нејзиното решение (десно)
Пожелно е да се почне со составување на поедноставни фигури, а за учениците од пониските одделенија, за почеток да им се даде сликата со решението на танграмот, и да се побара од нив самите да ги разместат делчињата од танграмот според прикажаната шема. Во изворите на крајот од оваа статија, може да најдете линкови до страници со танграмски сложувалки за почетници.
3. Примена на танграмите во наставата по математика
На првиот час со примена на танграмите, откако ќе се направат делчињата на танграмот, може да се премине на следните активности (дадени преку прашања и задачи). Видот на прашањата и задачите и нивната тежина и обем би требало да варира во зависност од возраста на учениците.
1. Именувај ги делчињата на танграмот. (2 „големи“ рамнокраки правоаголни триаголници, 1 „среден“ рамнокрак правоаголен триаголник, 2 „мали“ рамнокраки правоаголни триаголници, 1 квадрат и 1 паралелограм)
2. Може ли да составиш квадрат од само две делчиња од танграмот? (се составува од двата големи триаголници кога ќе се спојат со најдолгите страни)
3. Може ли да составиш квадрат од точно три делчиња од танграмот? (се составува од едниот среден триаголник и двата мали триаголници кои се поставуваат со нивните пократки страни по должината на најдолгата страна на средниот триаголник)
4. Може ли да составиш квадрат од точно 4 делчиња од танграмот? А од точно 5 делчиња? На колку различни начини може да го направиш тоа?
5. Дали постои друг начин на составување на квадрат од сите 7 делчиња на танграмот?
Понатаму, танграмите може да послужат за увежбување на плоштина на геометриски слики. Еве неколку прашања и задачи.
Нека секој мал квадрат на мрежата од која се изработуваат делчињата на танграмот има плоштина од 1 квадратна единица (кв. ед.).
1. Најди ја плоштината на секој од 7-те делчиња на танграмот. (плоштините на големите триаголници се по 4 кв. ед., на средниот триаголник е 2 кв. ед., на малите триаголници се по 1 кв. ед., на квадратот е 2 кв. ед. и на паралелограмот е 2 кв. ед.)
2. Кој дел од плоштината на танграмскиот квадрат е плоштината на секое од делчињата? (плоштините на големите триаголници се по 1/4 од плоштината на танграмскиот квадрат, на средниот триаголник е 1/8, на малите триаголници се по 1/16, на квадратот е 1/8 и на паралелограмот е 1/8)
3. Колку изнесува плоштината на една танграмска сложувалка составена од сите 7 делчиња на танграмот (дадете пример на сложувалка)? (одговорот е едноставен, исто колку и плоштината на танграмскиот квадрат, односно 16 кв. ед.)
Исто така, кога веќе се увежбуваат плоштините на геметриските слики, корисно би било учениците да видат дека со два комплета танграми (14 танграмски делчиња: 4 големи триаголници, 2 средни триаголници, 4 мали триаголници, 2 квадрата и 2 паралелограма) може да се илустрира Питагоровата теорема.
3. Примена на танграмите во наставата по математика
На првиот час со примена на танграмите, откако ќе се направат делчињата на танграмот, може да се премине на следните активности (дадени преку прашања и задачи). Видот на прашањата и задачите и нивната тежина и обем би требало да варира во зависност од возраста на учениците.
1. Именувај ги делчињата на танграмот. (2 „големи“ рамнокраки правоаголни триаголници, 1 „среден“ рамнокрак правоаголен триаголник, 2 „мали“ рамнокраки правоаголни триаголници, 1 квадрат и 1 паралелограм)
2. Може ли да составиш квадрат од само две делчиња од танграмот? (се составува од двата големи триаголници кога ќе се спојат со најдолгите страни)
3. Може ли да составиш квадрат од точно три делчиња од танграмот? (се составува од едниот среден триаголник и двата мали триаголници кои се поставуваат со нивните пократки страни по должината на најдолгата страна на средниот триаголник)
4. Може ли да составиш квадрат од точно 4 делчиња од танграмот? А од точно 5 делчиња? На колку различни начини може да го направиш тоа?
5. Дали постои друг начин на составување на квадрат од сите 7 делчиња на танграмот?
Понатаму, танграмите може да послужат за увежбување на плоштина на геометриски слики. Еве неколку прашања и задачи.
Нека секој мал квадрат на мрежата од која се изработуваат делчињата на танграмот има плоштина од 1 квадратна единица (кв. ед.).
1. Најди ја плоштината на секој од 7-те делчиња на танграмот. (плоштините на големите триаголници се по 4 кв. ед., на средниот триаголник е 2 кв. ед., на малите триаголници се по 1 кв. ед., на квадратот е 2 кв. ед. и на паралелограмот е 2 кв. ед.)
2. Кој дел од плоштината на танграмскиот квадрат е плоштината на секое од делчињата? (плоштините на големите триаголници се по 1/4 од плоштината на танграмскиот квадрат, на средниот триаголник е 1/8, на малите триаголници се по 1/16, на квадратот е 1/8 и на паралелограмот е 1/8)
3. Колку изнесува плоштината на една танграмска сложувалка составена од сите 7 делчиња на танграмот (дадете пример на сложувалка)? (одговорот е едноставен, исто колку и плоштината на танграмскиот квадрат, односно 16 кв. ед.)
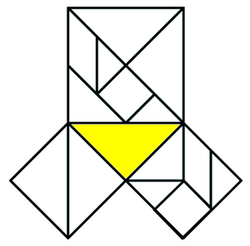
Исто така, кога веќе се увежбуваат плоштините на геметриските слики, корисно би било учениците да видат дека со два комплета танграми (14 танграмски делчиња: 4 големи триаголници, 2 средни триаголници, 4 мали триаголници, 2 квадрата и 2 паралелограма) може да се илустрира Питагоровата теорема.
Слика 3. Илустрација на Питагоровата теорема со два комплета танграми
Ги поттикнуваме наставниците да ги раскажат своите искуства или да дадат свој прилог задачи и решенија во врска со примената на танаграмите во наставата по математика и при развивањето на математичкото мислење.
4. Наместо заклучок...
Покрај увежбувањето на својствата на геометриските фигури, добро е да се знае дека танграмите служат и за поттикнување на креативноста за што сведочат и следните фотографии на полици за книги инспирирани од делчињата на танграмот.
4. Наместо заклучок...
Покрај увежбувањето на својствата на геометриските фигури, добро е да се знае дека танграмите служат и за поттикнување на креативноста за што сведочат и следните фотографии на полици за книги инспирирани од делчињата на танграмот.
Креативноста нема граници. Десертот секогаш доаѓа на крајот...
Едноставно е да се подготви: Земете едно квадратно парче леб. Отстранете ја кората. Од добиениот квадрат исечете ги со нож танграмските делчиња. Премачкајте ги со еурокрем (или некој друг намаз по желба). Составете фигура од танграмските делчиња и сервирајте ја со соодветна декорација. Пријатен апетит!
Извори:
[1] Centre for Innovation in Mathematics Teaching, Tangrams - Introduction, http://www.cimt.plymouth.ac.uk/resources/puzzles/tangrams/tangint.htm
[2] Tech it Out UK, Tangram History, http://www.techitoutuk.com/projects/tangrams/history.html
[3] Activity Village, Tangrams, http://www.activityvillage.co.uk/tangrams
[4] Education.com, Easy Tangrams Puzzles, http://www.education.com/slideshow/easy-tangrams-puzzles/
Автор:
Ирена Стојковска, Институт за математика, Природно математички факултет, Скопје
Објавено на ПОИМ:
11 јануари 2015
Начин на цитирање на статијата:
И. Стојковска, Танграми: Поглед кон математиката на еден креативен начин, Портал ПОИМ на Институтот за математика, ПМФ, Скопје, 11 јануари 2015, http://poim-pmf.weebly.com/tangrami.html
Извори:
[1] Centre for Innovation in Mathematics Teaching, Tangrams - Introduction, http://www.cimt.plymouth.ac.uk/resources/puzzles/tangrams/tangint.htm
[2] Tech it Out UK, Tangram History, http://www.techitoutuk.com/projects/tangrams/history.html
[3] Activity Village, Tangrams, http://www.activityvillage.co.uk/tangrams
[4] Education.com, Easy Tangrams Puzzles, http://www.education.com/slideshow/easy-tangrams-puzzles/
Автор:
Ирена Стојковска, Институт за математика, Природно математички факултет, Скопје
Објавено на ПОИМ:
11 јануари 2015
Начин на цитирање на статијата:
И. Стојковска, Танграми: Поглед кон математиката на еден креативен начин, Портал ПОИМ на Институтот за математика, ПМФ, Скопје, 11 јануари 2015, http://poim-pmf.weebly.com/tangrami.html
Download (PDF)
Авторизираните статии објавени на Порталот подлежат на законска заштита. Се забранува користење на статиите без наведување на авторот или изворот.