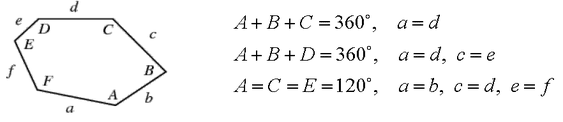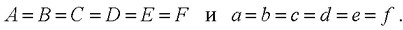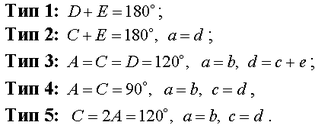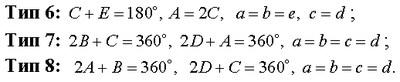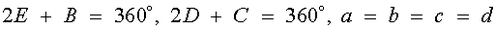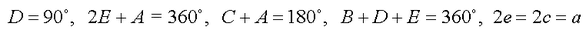СТАТИИ ЗА НАСТАВАТА ПО МАТЕМАТИКАСе залагаме за зголемување на свеста за местото и улогата на математиката во науките, технологијата, наставата, природата и културата.
|
ПАРКЕТИРАЊЕ СО ПЕТАГОЛНИЦИ
Ако една рамна површина може да се покрие користејќи само идентични копии на една иста рамнинска фигура, без да се остава простор измеѓу и без да има преклопување, тогаш велиме дека таа фигура ја паркетира рамнината. Општо познато е дека секој триаголник и секој четириаголник, било да е конвексен или не, може да паркетира една рамнина.
Во 1963 година покажано е дека има точно 3 типа конвексни неправилни шестаголници со кои може да се паркетира рамнина. Тоа се следните шестаголници:
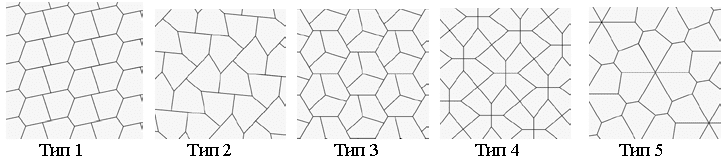
Равенките што ги опишуваат овие три типа шестаголници, ако шестаголникот е зададен со елементи како на цртежот подолу, се:
Се разбира, паркетирањето со правилни шестаголници (како на цртежот десно), е специјален случај на сите три паркетирања за
Ниту еден конвексен седумаголник, осумаголник или кој било друг n-аголник (n>8) не паркетира рамнина.
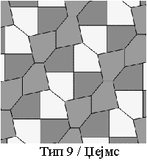
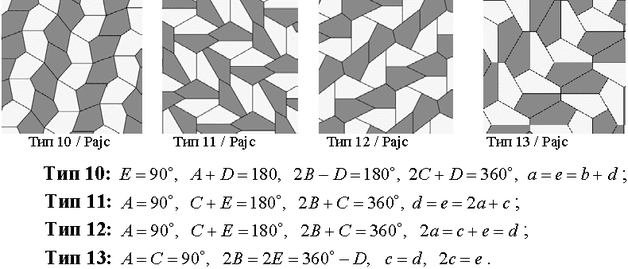
Работите стануваат поинтересни кога се работи за петаголници. Правилен петаголник не може да паркетира рамнина, но тоа може да се направи со помош на некои неправилни конвексни петаголници. Имено, потрагата и класифицирањето на неправилните конвексни петаголници со кои може да се паркетира рамнина трае скоро еден век. Овој интересен проблем, чија формулација може да ја разбере и дете, има богата историја. Таа се врзува со осумнаесетиот од славните Хилбертови 23 проблеми. Решавањето на проблемот започнува со германскиот математичар Карл Рајнхард (Karl Reinhardt, 1895 - 1941) кој во 1918 година открил 5 типа конвексни петаголници со кои може да се паркетира рамнина. Да појасниме: тој не открил 5 петаголника, туку открил 5 класи петаголници при што секоја од нив може да се опише со равенки. На цртежите се дадени по еден претставник од секоја класа петаголници на Рајнхард:
Работите стануваат поинтересни кога се работи за петаголници. Правилен петаголник не може да паркетира рамнина, но тоа може да се направи со помош на некои неправилни конвексни петаголници. Имено, потрагата и класифицирањето на неправилните конвексни петаголници со кои може да се паркетира рамнина трае скоро еден век. Овој интересен проблем, чија формулација може да ја разбере и дете, има богата историја. Таа се врзува со осумнаесетиот од славните Хилбертови 23 проблеми. Решавањето на проблемот започнува со германскиот математичар Карл Рајнхард (Karl Reinhardt, 1895 - 1941) кој во 1918 година открил 5 типа конвексни петаголници со кои може да се паркетира рамнина. Да појасниме: тој не открил 5 петаголника, туку открил 5 класи петаголници при што секоја од нив може да се опише со равенки. На цртежите се дадени по еден претставник од секоја класа петаголници на Рајнхард:
Нивните равенки се:
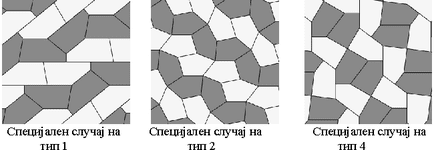
Во секоја од овие класи спаѓаат и разни специјални случаи, како на пример, случаите кога две од станите на петаголникот се паралелни. Такви се, на пример овие:
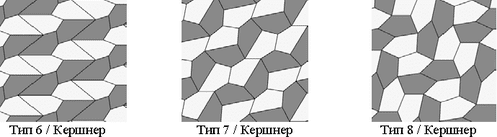
Многумина сметале дека Рајнхардовата листа е комплетна, кога во 1968 година Р. Б. Кершнер (R. B. Kershner) открил уште три.
Кершнеровите петаголници се зададени со равенките:
Во 1975 година, Ричард Џејмс (Richard James) открил уште еден тип петаголни паркети чии равенки се:
Истата година, Марџори Рајс (Marjorie Rice) домаќинка од Сан Диего, САД, ја прочитала статијата за Џејмсовото откритие во списанието Scientific American. Како математичар аматер, во периодот од 1976 до 1977 година, успеала да открие уште четири типа петаголници што паркетираат рамнина.
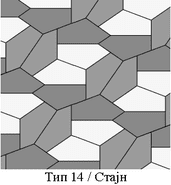
Во 1985 година Ролф Стајн (Rolf Stein) го открил четиринаесеттиот тип чии равенки се:
Но, трагата остинала, сè до пред една година, кога тројца истражувачи од универзитетот во Вашингтон, Кејси Ман, Џенифер Меклауд и Дејвид Вон Дероу (во оригинал: Casey Mann, Jennifer McLoud и David Von Derau), го откриле петнаесеттиот тип користејќи компјутерско пребарување низ разни можности. Овој петаголник има агли од 60, 135, 105, 90, 150 степени, а неговите страни ги задоволуваат равенствата
a = c = e, b = 2a.
Сè уште не знаеме дали овие се сите петаголни конвексни паркети и дали има уште што чекаат да бидат откриени.
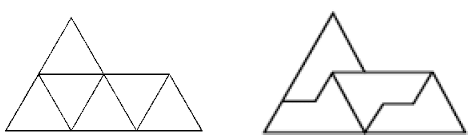
Една рамнина може да се паркетира и со неконвексни петаголници. Такво е, на пример, сфингиното паркетирање каде што се користи неконвексен петаголник формиран од шест рамнострани триаголници. Сфингата може да ја паркетира рамнината периодично, местејќи две сфинги една до друга за да формираат паралелограм (како на сликата долу десно). Потоа рамнината се паркетира со транслација на овој паралелограм.
Една рамнина може да се паркетира и со неконвексни петаголници. Такво е, на пример, сфингиното паркетирање каде што се користи неконвексен петаголник формиран од шест рамнострани триаголници. Сфингата може да ја паркетира рамнината периодично, местејќи две сфинги една до друга за да формираат паралелограм (како на сликата долу десно). Потоа рамнината се паркетира со транслација на овој паралелограм.
Испитувањето на петаголните паркети е интересно заради нивната потенцијална примена. Многу структури во природата, од кристалите до вирусите, се изградени од блокови што се принудени геометриски да се поврзат во една целина која би изградила една нова структура. Примената е неизбежна и во архитектурата, но и во фармацијата, зашто многу хемиски соединенија се создаваат од хемиски градбени блокови.
Литература:
[1] Maths in a minute: Tiling troubles, + Plus Magazine, 25 август 2015
[2] Jaap Scherphius, Pentagon Tilngs, www.jaapsch.net/tilings
[3] Martin Gardner, Time Travel and Other Mathematical Bewilderments: W. H. Freeman and Co., (1988) 163-176.
[4] Eyder Peralta, With Discovery, 3 Scientists Chip Away at an Unsolvable Math Problem
[5] Кит Девлин, Милениумските проблеми, Магор, 2005
[6] Ivan Niven, Convex Polygons that Cannot Tile the Plane, The American Mathematical Monthly, Vol. 85, No. 10 (Dec., 1978), pp. 785-792
[7] Teruhisa Sugimoto, Tohru Ogawa, Tiling Problem of Convex Pentagon, Forma, 15, 75–79, 2000
[1] Maths in a minute: Tiling troubles, + Plus Magazine, 25 август 2015
[2] Jaap Scherphius, Pentagon Tilngs, www.jaapsch.net/tilings
[3] Martin Gardner, Time Travel and Other Mathematical Bewilderments: W. H. Freeman and Co., (1988) 163-176.
[4] Eyder Peralta, With Discovery, 3 Scientists Chip Away at an Unsolvable Math Problem
[5] Кит Девлин, Милениумските проблеми, Магор, 2005
[6] Ivan Niven, Convex Polygons that Cannot Tile the Plane, The American Mathematical Monthly, Vol. 85, No. 10 (Dec., 1978), pp. 785-792
[7] Teruhisa Sugimoto, Tohru Ogawa, Tiling Problem of Convex Pentagon, Forma, 15, 75–79, 2000
Автор:
Весна Целакоска-Јорданова, Институт за математика, Природно математички факултет, Скопје
Објавено на ПОИМ:
20 февруари 2017
Начин на цитирање на статијата:
В. Целакоска-Јорданова, Паркетирање со петаголници, Портал ПОИМ на Институтот за математика, ПМФ, Скопје, 20 февруари 2017, http://poim-pmf.weebly.com/parketiranje-so-petagolnici.html
Dowload (PDF)
Весна Целакоска-Јорданова, Институт за математика, Природно математички факултет, Скопје
Објавено на ПОИМ:
20 февруари 2017
Начин на цитирање на статијата:
В. Целакоска-Јорданова, Паркетирање со петаголници, Портал ПОИМ на Институтот за математика, ПМФ, Скопје, 20 февруари 2017, http://poim-pmf.weebly.com/parketiranje-so-petagolnici.html
Dowload (PDF)
Авторизираните статии објавени на Порталот подлежат на законска заштита. Се забранува користење на статиите без наведување на авторот или изворот.