НАУЧНО - ПОПУЛАРНИ СТАТИИСе залагаме за зголемување на свеста за местото и улогата на математиката во науките, технологијата, наставата, природата и културата.
|
Прочитајте математички трилер!
„СТРИКО ПЕТРОС И ГОЛДБАХОВАТА ХИПОТЕЗА“
ОД АПОСТОЛОС ДОКСИАДИС
|
Оваа возбудлива книга, којашто го остава читателот без здив до последната страница и која, за жал, не е преведена на македонски јазик, ни го приближува духот на математиката и истражувањата во математиката. Тaа претставува една математичка детективска приказна за потрагата по одговорот на една мистерија...Голдбаховата хипотеза. Тоа е најстариот и најпознатиот нерешен проблем од теоријата на броеви и општо, од математиката. За оние коишто не ја знаат, таа гласи:
СЕКОЈ ПАРЕН БРОЈ ПОГОЛЕМ ОД 2 МОЖЕ ДА СЕ ПРЕТСТАВИ КАКО ЗБИР ОД ДВА ПРОСТИ БРОЈА.
Интересно е да се спомене дека Кристијан Голдбах ја формулирал хипотезата (позната и како бинарна) на 7 јуни 1742 година (во едно писмо упатено до Ојлер) на следниов начин:
Секој природен број поголем од 2 може да се претстави како збир од три прости броеви.
|
Голдбах го сметал и бројот 1 за прост број, што од денешна гледна точка не е вообичаено. Малку е познато, дури и меѓу математичарите, дека Голдбаховата хипотеза во денешната форма ја дал Ојлер. Неговата забелешка била во следнава форма: кога би било така, т.е. кога секој природен број поголем од 2, би се претставувал како збир од три прости броеви, тогаш, ако станува збор за парен број, еден од тие три прости броеви би бил 2 (зашто збирот на три непарни прости броеви е непарен број, а само 2 е парен број). Очигледен е заклучокот дека секој парен број поголем од 2 може да се претстави како збир на два прости броја. Ојлер бил уверен дека оваа хипотеза е точна, само што не успеал да ја докаже.
Покрај бинарната Голдбахова хипотеза, позната е и тернарната Голбахова хипотеза:
Покрај бинарната Голдбахова хипотеза, позната е и тернарната Голбахова хипотеза:
Секој непарен природен број поголем од 5 може да се претстави како збир од три прости броја.
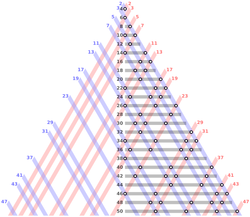
Слика 1. Паровите прости броеви на коишто се разложуваат првите 24 парни броеви
Но, да се вратиме на делото. Тоа започнува со една мисла на Харди од неговата книга „Извинување на еден математичар“:
На Архимед ќе се сеќаваат и кога Есхила ќе го заборават, зашто јазиците умираат, а математичките идеи не. Зборот „бесмртност“ можеби е смешен, но математичарите за неа имаат најголеми изгледи, што и да значи тоа.
Делото започнува со описот на необичниот, ексцентричниот стрико Петрос (полното име му е Петрос Папахристос), кој живее осамено и главно деновите ги поминува со своите книги и играјќи шах. Тој е прикажан како отпадник, како црна овца на семејството, а зошто е тоа така, ни раскажува неговиот внук. Петрос Папахристос бил надарен математичар, кој целиот свој живот, почнувајки од студиите во Германија кај познатиот професор Каратеодори, го посветил на својата опсесија: докажувањето на Голдбаховата хипотеза. Од Германија заминал за Англија, а таму соработувал со познатите личности од теоријата на броеви: Харди, Литлвуд и самоукиот математички гениј Сриниваса Рамануџан. Но, сакајќи ја славата само за себе, тој се изолирал од сите: заминал на универзитетот во Минхен и таму работел сам, притоа доаѓајќи до разни меѓурезултати коишто не се осмелил да ги објави, за некој да не му ја преземе работата и славата. Потоа, тој се повлекол во едно село во предградието на Атина и таму, грозничаво ја продолжил својата работа. Таму го открил шахот, како игра што го релаксира мозокот и овозможува подлабока концентрација. Во меѓувреме, неговиот внук, кој студирал економија/математика во Америка, ја открил вистината за својот стрико. Тој му е лут зашто го натерал цело лето да ја решава Голдбаховата хипотеза, без да користи никаква литература и никаква помош. Но, лутината спаѓа и по завршувањето на студиите, тој често оди кај својот стрико, да ја слуша приказната за неговиот живот и напредокот во работата. На крајот на делото, слично како во анегдотата за доказот на маргината на последната теорема на Ферма, остануваме во недоумица. Петрос Папахристос умира докажувајќи ја теоремата, но не остава зад себе никаков пишан документ. На неговата надгробна плоча, неговиот омилен внук дал да се исклеса Голдбаховата хипотеза онака како што гласи.
Во делото се спомнуваат и други, многу познати проблеми, како што се на пример, последната теорема на Ферма (којашто ја докажал Ендру Вајлс (Andrew Wiles) во 1995 година, а кој во последниот период на својата работа соработувал со Ричард Тејлор (Richard Taylor)) и Римановата хипотеза (којашто сé уште не е докажана). Се спомнува и дека Харди ја докажал тернарната Голдбахова хипотеза, само што неговиот доказ има една голема мана: ја користи Римановата хипотеза.
Покрај тоа, се спомнуваат многу математичари, како на пример, Каратеодори, Харди, Литлвуд, Рамануџан, Гедел, Тјуринг, Кронекер, Галоа, Ојлер,Ферма ... како и познати и помалку познати анегдоти поврзани со нив.
Искрено ја препорачувам оваа математичка лектира на сите, и на оние кои знаат математика и на оние коишто математиката ја сметаат само за тежок училиштен предмет. И, за крај, книгата изобилува со прекрасни мисли за животот и математиката и овде ќе цитираме некои од нив (преводот од хрватски го прави авторот на оваа статија).
Вистинската математика нема никаква врска со примената, а ни со пресметувањата кои ги учиш на училиште. Таа проучува апстрактни интелектуални конструкти, кои, барем додека математичарот е окупиран со нив, ни во најмал дел не го допираат физичкиот, сетилниот свет.
Математичарите имаат подеднакво задоволство од своето проучување како и шахистите во шахот. Поточно, психолошкиот профил на вистинскиот математичар е поблизок до поетот или композиторот, со други зборови, до некој кој се занимава со создавање Убавина и којшто е во потрага по Складот и Совршенството. Тој е дијаметрална спротивност на практичниот човек, инженерот, политичарот или... – застана за миг, барајќи нешто пониско на својата вредносна скала - ... всушност, бизнисменот.
Знаеш ли што одговорил Давид Хилберт кога колегите го прашале зошто никогаш не се обидел да ја докаже таканаречената „Последна теорема на Ферма“? ... Рекол: „Зошто да ја убиеш кокошката што несе златни јајца?“ Мислел, гледаш, на тоа дека секогаш кога големите математичари се обидуваат да решат големи проблеми, се создава одлична математика – таканаречени „меѓурезултати“, дури и кога почетниот проблем останува нерешен.
Осаменоста на истражувачот кој се бави со изворни математички сознанија не може да се спореди со ниедна друга осаменост. ...Тој живее во потполно непристапен свет и за пошироката јавност и за поблиската околина. Дури ни оние што му се најблиски не можат да учествуваат ниту во неговата среќа ниту во неговата тага, на ниеден битен начин, зашто им е просто невозможно да ја разберат нивната содржина. Единствено друштво на коешто може вистински да припаѓа еден математичар, е друштвото на своите колеги...
... Клучно за еден математичар е да проведува време подалеку од проблемот со кој се бави. За да може умот да ја свари направената работа и да ги обработи неговите резултати на несвесно ниво, му треба опуштање, исто толку колку што му треба оптоварување. Колку и да е освежувачко истражувањето на математичките идеи за мирниот ум, толку тоа може да стане и неподносливо кога мозокот му е преплавен со умор и исцрпен од постојано напрегање.
Теоремите до кои се доаѓа со строги докази, навистина се апсолутни и вечни, но методите со кои до нив се доаѓа, воопшто не се. Тие се само избор на математичарот условен од околностите – и всушност затоа се менуваат толку често.
За жал, во математиката не постои сребрен медал. Првиот што ќе разгласи и објави, ја добива целата слава. За вториот не останува ништо.
Математиката е како стебло со цврсти корени (аксиоми), масивно стебло (строг доказ) и гранки коишто постојано се шират и на кои цветаат чудесни цветови (теореми).
Да научиш малку вистинска математика, дури и само мал дел, за мене беше непроценливо вредна животна поука. ... Нематематичар не може да сфати каква среќа му е ускратена. Мешавина на Вистината и Убавината која се открива со разбирање на некоја важна теорема, не може да се открие со ниту една друга активност, освен со (не би знаел точно) мистичните религии.
На оние што не се стручни, морам на ова место да им кажам дека во математичките книги не може нормално да се ужива како во романите, в кревет, во када, навален на мек наслон или наслонет на комода. Овде „да читаш“ значи да разбираш, а за тоа обично ви е потребна тврда подлога, хартија, молив и многу време.
Оние што сакаат да дознаат повеќе за оваа книга, за Голдбаховата хипотеза, за Хардиевата книга „Извинување на еден математичар“, за милениумските проблеми, можат да ги погледнат следните линкови:
[1] Stric Petros i Goldbahova slutnja / Najbolje knjige
[2] Goldbach Conjecture / Wolfram Math World
[3] Goldbach Conjecture, The Prime Glossary
[4] Hardy: A Mathematician's Apology
[5] Милениумските проблеми - Кит Девлин
[6] Apostolos Doxiadis / Biography
Автор:
Весна Целакоска-Јорданова, Институт за математика, Природно математички факултет, Скопје
Објавено на ПОИМ:
31 јануари 2015
Начин на цитирање на статијата:
В. Целакоска-Јорданова, Прочитајте математички трилер! „Срико Петрос и Голдбаховата хипотеза“ од Апостолос Доксиадис, Портал ПОИМ на Институтот за математика, ПМФ, Скопје, 9 јануари 2015, http://poim-pmf.weebly.com/matematicki-triler.html
На Архимед ќе се сеќаваат и кога Есхила ќе го заборават, зашто јазиците умираат, а математичките идеи не. Зборот „бесмртност“ можеби е смешен, но математичарите за неа имаат најголеми изгледи, што и да значи тоа.
Делото започнува со описот на необичниот, ексцентричниот стрико Петрос (полното име му е Петрос Папахристос), кој живее осамено и главно деновите ги поминува со своите книги и играјќи шах. Тој е прикажан како отпадник, како црна овца на семејството, а зошто е тоа така, ни раскажува неговиот внук. Петрос Папахристос бил надарен математичар, кој целиот свој живот, почнувајки од студиите во Германија кај познатиот професор Каратеодори, го посветил на својата опсесија: докажувањето на Голдбаховата хипотеза. Од Германија заминал за Англија, а таму соработувал со познатите личности од теоријата на броеви: Харди, Литлвуд и самоукиот математички гениј Сриниваса Рамануџан. Но, сакајќи ја славата само за себе, тој се изолирал од сите: заминал на универзитетот во Минхен и таму работел сам, притоа доаѓајќи до разни меѓурезултати коишто не се осмелил да ги објави, за некој да не му ја преземе работата и славата. Потоа, тој се повлекол во едно село во предградието на Атина и таму, грозничаво ја продолжил својата работа. Таму го открил шахот, како игра што го релаксира мозокот и овозможува подлабока концентрација. Во меѓувреме, неговиот внук, кој студирал економија/математика во Америка, ја открил вистината за својот стрико. Тој му е лут зашто го натерал цело лето да ја решава Голдбаховата хипотеза, без да користи никаква литература и никаква помош. Но, лутината спаѓа и по завршувањето на студиите, тој често оди кај својот стрико, да ја слуша приказната за неговиот живот и напредокот во работата. На крајот на делото, слично како во анегдотата за доказот на маргината на последната теорема на Ферма, остануваме во недоумица. Петрос Папахристос умира докажувајќи ја теоремата, но не остава зад себе никаков пишан документ. На неговата надгробна плоча, неговиот омилен внук дал да се исклеса Голдбаховата хипотеза онака како што гласи.
Во делото се спомнуваат и други, многу познати проблеми, како што се на пример, последната теорема на Ферма (којашто ја докажал Ендру Вајлс (Andrew Wiles) во 1995 година, а кој во последниот период на својата работа соработувал со Ричард Тејлор (Richard Taylor)) и Римановата хипотеза (којашто сé уште не е докажана). Се спомнува и дека Харди ја докажал тернарната Голдбахова хипотеза, само што неговиот доказ има една голема мана: ја користи Римановата хипотеза.
Покрај тоа, се спомнуваат многу математичари, како на пример, Каратеодори, Харди, Литлвуд, Рамануџан, Гедел, Тјуринг, Кронекер, Галоа, Ојлер,Ферма ... како и познати и помалку познати анегдоти поврзани со нив.
Искрено ја препорачувам оваа математичка лектира на сите, и на оние кои знаат математика и на оние коишто математиката ја сметаат само за тежок училиштен предмет. И, за крај, книгата изобилува со прекрасни мисли за животот и математиката и овде ќе цитираме некои од нив (преводот од хрватски го прави авторот на оваа статија).
Вистинската математика нема никаква врска со примената, а ни со пресметувањата кои ги учиш на училиште. Таа проучува апстрактни интелектуални конструкти, кои, барем додека математичарот е окупиран со нив, ни во најмал дел не го допираат физичкиот, сетилниот свет.
Математичарите имаат подеднакво задоволство од своето проучување како и шахистите во шахот. Поточно, психолошкиот профил на вистинскиот математичар е поблизок до поетот или композиторот, со други зборови, до некој кој се занимава со создавање Убавина и којшто е во потрага по Складот и Совршенството. Тој е дијаметрална спротивност на практичниот човек, инженерот, политичарот или... – застана за миг, барајќи нешто пониско на својата вредносна скала - ... всушност, бизнисменот.
Знаеш ли што одговорил Давид Хилберт кога колегите го прашале зошто никогаш не се обидел да ја докаже таканаречената „Последна теорема на Ферма“? ... Рекол: „Зошто да ја убиеш кокошката што несе златни јајца?“ Мислел, гледаш, на тоа дека секогаш кога големите математичари се обидуваат да решат големи проблеми, се создава одлична математика – таканаречени „меѓурезултати“, дури и кога почетниот проблем останува нерешен.
Осаменоста на истражувачот кој се бави со изворни математички сознанија не може да се спореди со ниедна друга осаменост. ...Тој живее во потполно непристапен свет и за пошироката јавност и за поблиската околина. Дури ни оние што му се најблиски не можат да учествуваат ниту во неговата среќа ниту во неговата тага, на ниеден битен начин, зашто им е просто невозможно да ја разберат нивната содржина. Единствено друштво на коешто може вистински да припаѓа еден математичар, е друштвото на своите колеги...
... Клучно за еден математичар е да проведува време подалеку од проблемот со кој се бави. За да може умот да ја свари направената работа и да ги обработи неговите резултати на несвесно ниво, му треба опуштање, исто толку колку што му треба оптоварување. Колку и да е освежувачко истражувањето на математичките идеи за мирниот ум, толку тоа може да стане и неподносливо кога мозокот му е преплавен со умор и исцрпен од постојано напрегање.
Теоремите до кои се доаѓа со строги докази, навистина се апсолутни и вечни, но методите со кои до нив се доаѓа, воопшто не се. Тие се само избор на математичарот условен од околностите – и всушност затоа се менуваат толку често.
За жал, во математиката не постои сребрен медал. Првиот што ќе разгласи и објави, ја добива целата слава. За вториот не останува ништо.
Математиката е како стебло со цврсти корени (аксиоми), масивно стебло (строг доказ) и гранки коишто постојано се шират и на кои цветаат чудесни цветови (теореми).
Да научиш малку вистинска математика, дури и само мал дел, за мене беше непроценливо вредна животна поука. ... Нематематичар не може да сфати каква среќа му е ускратена. Мешавина на Вистината и Убавината која се открива со разбирање на некоја важна теорема, не може да се открие со ниту една друга активност, освен со (не би знаел точно) мистичните религии.
На оние што не се стручни, морам на ова место да им кажам дека во математичките книги не може нормално да се ужива како во романите, в кревет, во када, навален на мек наслон или наслонет на комода. Овде „да читаш“ значи да разбираш, а за тоа обично ви е потребна тврда подлога, хартија, молив и многу време.
Оние што сакаат да дознаат повеќе за оваа книга, за Голдбаховата хипотеза, за Хардиевата книга „Извинување на еден математичар“, за милениумските проблеми, можат да ги погледнат следните линкови:
[1] Stric Petros i Goldbahova slutnja / Najbolje knjige
[2] Goldbach Conjecture / Wolfram Math World
[3] Goldbach Conjecture, The Prime Glossary
[4] Hardy: A Mathematician's Apology
[5] Милениумските проблеми - Кит Девлин
[6] Apostolos Doxiadis / Biography
Автор:
Весна Целакоска-Јорданова, Институт за математика, Природно математички факултет, Скопје
Објавено на ПОИМ:
31 јануари 2015
Начин на цитирање на статијата:
В. Целакоска-Јорданова, Прочитајте математички трилер! „Срико Петрос и Голдбаховата хипотеза“ од Апостолос Доксиадис, Портал ПОИМ на Институтот за математика, ПМФ, Скопје, 9 јануари 2015, http://poim-pmf.weebly.com/matematicki-triler.html
Download (PDF)
Авторизираните статии објавени на Порталот подлежат на законска заштита. Се забранува користење на статиите без наведување на авторот или изворот.