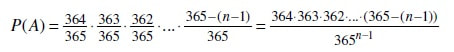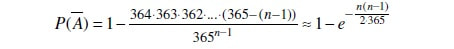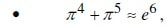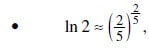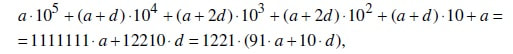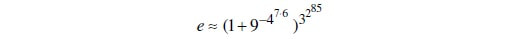НАУЧНО - ПОПУЛАРНИ СТАТИИСе залагаме за зголемување на свеста за местото и улогата на математиката во науките, технологијата, наставата, природата и културата.
|
МАТЕМАТИЧКИ ПОГЛЕД НА КОИНЦИДЕНЦИИТЕ

„Пред малку само што помислив на тебе, и ти тукушто ми се јави! Каква коинциденција!“ Дали сте се нашле некогаш, во ваква или во слична ситуација? Да бидете сведоци на реализација на многу редок, неочекуван, навидум невозможен настан? Нема да погрешиме ако претпоставиме дека секој од нас доживеал нешто слично во животот и тоа можеби повеќе од еднаш. Но, дали треба коинциденциите да нè изненадуваат? Да почнеме со ред.
Чудно би било кога не би имало коинциденции
Ќе се обидеме да дадеме едноставен одговор на последното прашање, се надеваме разбирлив дури и за оние кои се почетници во терминологијата на теоријата на веројатност. Имено, има голем број настани кои е возможно да се случат и кои заслужуваат да ги наречеме „коинциденции“, да го означиме нивниот број со N. Тука спаѓаат телефонски повици или средби со стари пријатели кои многу оддамна не сте ги слушнале или виделе и тоа токму тогаш кога сте помислиле на нив; потоа совпаѓање на датуми на родендени, годишнини, таму каде што најмалку очекувате, па дури и немили настани како, на пример, погодување гром двапати на исто место и многу други. Нека секој од тие настани може да се случи со многу мала веројатност во текот на одреден период, да речеме една недела. Да ја означиме таа веројатност со p. Тогаш, производот Np го означува просечниот или очекуваниот број на појавувања на коинциденциите во тој период и за N големо и p мало, овој број може да биде со разумна големина, што ни дава математичко, т.е. веројатносно оправдување дека коинциденција сепак ќе случи, порано или подоцна.
Колку ретките настани се навистина ретки?
Како што видовме случувањето на коинциденциите има убаво објаснување во теоријата на веројатност. Доколку нив ги третираме како ретки настани - настани коишто имаат мала веројатност да се случат, но сепак нивното случување не е исклучено, горното објаснување значи дека ретките настани не треба да се занемаруваат, затоа што порано или подоцна некој редок настан може да се случи. Од друга страна, многу често, последиците од ретките настани се со огромни размери, па затоа стабилните држави не треба да се двоумат да инвестираат во реализација на програми за заштита од поплави, земјотреси и слични елементарни непогоди. Паралелно со тоа, осигурителните компании веќе задолжуваат актуари коишто треба да ги предвидат последиците, да изработат модели за справување со ретки настани.
Чудно би било кога не би имало коинциденции
Ќе се обидеме да дадеме едноставен одговор на последното прашање, се надеваме разбирлив дури и за оние кои се почетници во терминологијата на теоријата на веројатност. Имено, има голем број настани кои е возможно да се случат и кои заслужуваат да ги наречеме „коинциденции“, да го означиме нивниот број со N. Тука спаѓаат телефонски повици или средби со стари пријатели кои многу оддамна не сте ги слушнале или виделе и тоа токму тогаш кога сте помислиле на нив; потоа совпаѓање на датуми на родендени, годишнини, таму каде што најмалку очекувате, па дури и немили настани како, на пример, погодување гром двапати на исто место и многу други. Нека секој од тие настани може да се случи со многу мала веројатност во текот на одреден период, да речеме една недела. Да ја означиме таа веројатност со p. Тогаш, производот Np го означува просечниот или очекуваниот број на појавувања на коинциденциите во тој период и за N големо и p мало, овој број може да биде со разумна големина, што ни дава математичко, т.е. веројатносно оправдување дека коинциденција сепак ќе случи, порано или подоцна.
Колку ретките настани се навистина ретки?
Како што видовме случувањето на коинциденциите има убаво објаснување во теоријата на веројатност. Доколку нив ги третираме како ретки настани - настани коишто имаат мала веројатност да се случат, но сепак нивното случување не е исклучено, горното објаснување значи дека ретките настани не треба да се занемаруваат, затоа што порано или подоцна некој редок настан може да се случи. Од друга страна, многу често, последиците од ретките настани се со огромни размери, па затоа стабилните држави не треба да се двоумат да инвестираат во реализација на програми за заштита од поплави, земјотреси и слични елементарни непогоди. Паралелно со тоа, осигурителните компании веќе задолжуваат актуари коишто треба да ги предвидат последиците, да изработат модели за справување со ретки настани.
Да се вратиме на коинциденциите и нивното восприемање како ретки настани. Но, да видиме дали секоја коинциденција е редок настан. Роденденскиот проблем е класичен пример во теоријата на веројатност за тоа колку неочекуваното може да очекуваме да се случи, па затоа е познат и како роденденски парадокс. Проблемот гласи вака: „Под претпоставка дека родендените на луѓето се рамномерно распределени во една година од 365 дена, одреди ја веројатноста меѓу n случајно избрани луѓе, најмалку двајца да имаат роденден во ист ден.“ Па, ако со А го означиме настанот никои двајца од групата со n луѓе да немаат роденден во ист ден, тогаш веројатноста на тој настан е
каде што првиот множител е веројатноста вториот човек да нема роденден во ист ден со првиот, вториот множител е веројатноста третиот човек да нема роденден во ист ден ниту со првиот ниту со вториот, под претпоставка дека првите двајца немаат роденден во ист ден, и сè така до последниот, (n-1)-ви множител е веројатноста n-тиот човек да нема роденден во ист ден со никој од претходните (n-1) луѓе, под претпоставка дека секој од (n-1)-те луѓе има роденден во различен ден. Настанот чија веројатност ја бараме е впрочем спротивниот настан од настанот А т.е. најмалку двајца меѓу n случајно избрани луѓе да имаат роденден во ист ден, па неговата веројатност е
Последната апроксимација е корисна за приближно да ја пресметаме оваа веројатност за дадено n. Така, за n=5, ќе добиеме дека веројатноста најмалку двајца меѓу 5 случајно избрани луѓе да имаат роденден во ист ден е 0,0271 или 2,71%. Но, за n=23, веројатноста најмалку двајца меѓу 23 случајно избрани луѓе да имаат роденден во ист ден е 0,5 или 50%, додека за n=75, веројатноста најмалку двајца меѓу 75 случајно избрани луѓе да имаат роденден во ист ден е навистина голема, таа приближно иснесува 0,9995 или 99,95%. Овие бројки ни покажуваат дека колку и да ни изгледа редок настанот меѓу одредена група луѓе да сретнеме најмалку двајца кои имаат роденден во ист ден, сепак тоа и не е баш така „ретко“, имено веќе во група од 86-мина, со сигурност (до 4 децимали) може да очекуваме најмалку двајца да имаат роденден во ист ден - скоро сигурна коинциденција!
Сега, да го видоизмениме роденденскиот проблем во следниот облик: „Под претпоставка дека родендените на луѓето се рамномерно распределени во една година од 365 дена, одреди ја веројатноста меѓу n случајно избрани луѓе, најмалку еден да има роденден во ист ден како твојот роденден.“ Во овој случај добиваме настан со помала веројатност, за која исто така се покажува дека не е баш мала. Имено, потребни се најмалку 253 луѓе за со веројатност поголема од 1/2, односно поголема од 50%, да најдете барем еден кој има роденден во ист ден како вашиот. Имајќи го предвид проценетиот број пријатели и познаници на еден просечен човек, околу 600, не е воопшто чудно да се познавате најмалку со еден човек со кој делите ист роденден.
И математиката не е имуна на коинциденции
Коинциденциите се толку интересни за истражување што во математиката постои посебен термин „математичка коинциденција“. Под математичка коинциденција се подразбира еднаквост или приближна еднаквост на два израза за која нема теоретско објаснување (или сè уште не е најдено). Да наведеме некои од нив:
И математиката не е имуна на коинциденции
Коинциденциите се толку интересни за истражување што во математиката постои посебен термин „математичка коинциденција“. Под математичка коинциденција се подразбира еднаквост или приближна еднаквост на два израза за која нема теоретско објаснување (или сè уште не е најдено). Да наведеме некои од нив:
со точност до 4-та децимала,
со точност до 4-та децимала,
- 2^5 ∙ 9^2 = 2592, еден од многуте Фридманови броеви, броеви кои може да се запишат користејќи ги сите свои цифри точно еднаш, четирите основни операции, спротивен број, загради и степенување,
- броевите 31, 331, 3331, 33331, 333331, 3333331 и 33333331 се сите прости броеви, но веќе следниот број 333333331 = 17 ∙ 19607843 не е прост број,
- вкупниот број секунди во шест недели е 10!.
Повеќе математички коинциденции може да најдете на следниот линк. Но, дали секој „чуден“ математички исказ е навистина математичка коинциденција или е факт за кој постои математички доказ?
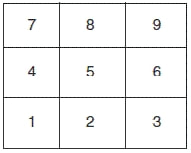
Да го погледнеме распоредот на цифрите од 1 до 9 на класичниот калкулатор.
Да го погледнеме распоредот на цифрите од 1 до 9 на класичниот калкулатор.
За шестцифрените броеви формирани со „читање“ на цифрите во секој ред, колона и двете дијагонали, во едната, па потоа во обратаната насока, односно за броевите: 123321, 321123, 456654, 654456, 789987, 987789, 147741, 741147, 258852, 852258, 369963, 963369, 159951, 951159, 357753 и 753357, важи дека секој од нив е делив со 37. Коинциденција или математички докажлив факт? Да забележиме дека првите три цифри на секој од овие броеви формираат аритметичка прогресија, па да ги изначиме со a, a + d и a + 2d. Тогаш, за броеви добиени на начинот како погоре имаме:
па не само што секој од нив е делив со 37, туку и со 1221.
Еве и една извонредно изненадувачка апроксимација на бројот е,
Еве и една извонредно изненадувачка апроксимација на бројот е,
и тоа со точност до 18457734525360901453873570-та децимала! Чудно е како некој воопшто дошол до овој факт. Математичко објаснување? Да. Постои. Оваа апроксимација е добиена со замена за n=3^(2^85) во низата (1+1/n)^n чија гранична вредност е бројот e. Тоа што сепак е за спомнување е тоа што во оваа апроксимација секоја од цифрите од 1 до 9 е искористена точно еднаш.
Коинциденција наместо заклучок
Верувајте во случувањата на коинциденциите, на чудата. Ви посакуваме многу среќни коинциденции во годината што иде!
Коинциденција наместо заклучок
- Првиот ден од 2018 година е во првиот ден од неделата - понеделник. Каква коинциденција!
Верувајте во случувањата на коинциденциите, на чудата. Ви посакуваме многу среќни коинциденции во годината што иде!
Извори:
[1] Geoffrey Grimmett, What a coincidence!, https://plus.maths.org/content/what-coincidence
[2] Marc Lange, What Are Mathematical Coincidences (and Why Does It Matter)? https://philosophy.unc.edu/files/2013/10/mathcoincMINDpublished.pdf
Автор:
Ирена Стојковска, Институт за математика, Природно-математички факултет, Скопје
Објавено на ПОИМ:
29 декември 2017
Начин на цитирање на статијата:
И. Стојковска, Математички поглед на коинциденциите, Портал ПОИМ на Институтот за математика, ПМФ, Скопје, 29 декември 2017, http://poim-pmf.weebly.com/matematicki-pogled-na-koincidenciite.html
Download (PDF)
Авторизираните статии објавени на Порталот подлежат на законска заштита. Се забранува користење на статиите без наведување на авторот или изворот.