НАУЧНО - ПОПУЛАРНИ СТАТИИСе залагаме за зголемување на свеста за местото и улогата на математиката во науките, технологијата, наставата, природата и културата.
|
КАКО СЕ ПРОЦЕНУВА БРОЈОТ НА ЛУЃЕ НА ЈАВНИ СОБИРИ

Понекогаш кога слушаме вести или читаме некој дневен весник наидуваме на изјави од типот: „На овој настан присуствуваа околу 15000 лица.“ Некој друг, за истиот тој настан, направил проценка од 7000 лица. Која е поточна? И како се прави една ваква проценка?
Методот за пресметување на бројот на луѓе на масовни собири го дал новинарот и професор по новинарство на Универзитетот Беркли во Калифорнија, Херберт Џејкобс (Herbert Jacobs, 1903-1987), на крајот од шеесетите години на минатиот век. Од прозорецот на својата канцеларија, Џејкобс ги гледал студентите што се собирале на плоштадот, протестирајќи против војната во Виетнам.
Бетонската подлога на овој плоштад e прошарана со квадратна решетка (сликата долу лево), па така Џејкобс ги пребројал студентите кои стоеле во некои од квадратите и го пресметал просечниот број на студенти во еден квадрат. Потоа го помножил тој број со вкупниот број квадрати од решетката.
Методот за пресметување на бројот на луѓе на масовни собири го дал новинарот и професор по новинарство на Универзитетот Беркли во Калифорнија, Херберт Џејкобс (Herbert Jacobs, 1903-1987), на крајот од шеесетите години на минатиот век. Од прозорецот на својата канцеларија, Џејкобс ги гледал студентите што се собирале на плоштадот, протестирајќи против војната во Виетнам.
Бетонската подлога на овој плоштад e прошарана со квадратна решетка (сликата долу лево), па така Џејкобс ги пребројал студентите кои стоеле во некои од квадратите и го пресметал просечниот број на студенти во еден квадрат. Потоа го помножил тој број со вкупниот број квадрати од решетката.
Плоштадот пред Универзитетот Беркли во Калифорнија, САД
Џејкобс извел одредени правила кои и денес се применуваат при проценка на посетеноста на собирите. Слабо посетен собир е оној каде што еден човек се наоѓа на распон на рацете до својот најблизок сосед. Приближно пресметано, тоа е еден човек на секој квадратен метар. Густо посетен собир е оној на којшто има по еден човек приближно на секои 0,42 квадратни метри, додека вистински страшна маса луѓе би имала еден човек на секоја четвртина квадратен метар или 0,25 квадратни метри.
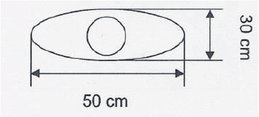
До слични бројки може да дојдеме и според расудувањата на д-р Дирк Оберхагеман (ориг.: Dirk Oberhagemann), германски истражувач и стручњак за однесување на толпа луѓе. Имено, еден просечен човек, заедно со својата облека, зафаќа 0,15 квадратни метри (види ја сликата долу). Тоа би значело дека максималната можна густина е 6,6 луѓе на метар квадратен. Меѓутоа, според него, реалноста покажала дека максималната густина на еден собир е четворица на метар квадратен, што повторно не' доведува до истата бројка од 0,25 квадратни метри за еден човек при максимално посетен собир.
До слични бројки може да дојдеме и според расудувањата на д-р Дирк Оберхагеман (ориг.: Dirk Oberhagemann), германски истражувач и стручњак за однесување на толпа луѓе. Имено, еден просечен човек, заедно со својата облека, зафаќа 0,15 квадратни метри (види ја сликата долу). Тоа би значело дека максималната можна густина е 6,6 луѓе на метар квадратен. Меѓутоа, според него, реалноста покажала дека максималната густина на еден собир е четворица на метар квадратен, што повторно не' доведува до истата бројка од 0,25 квадратни метри за еден човек при максимално посетен собир.
Местото што го зафаќа еден просечен човек стоејќи
Значи, ако ја имаме плоштината на вкупната површина, која денес лесно се наоѓа користејќи сателитски снимки на Google Earth, и ја поделиме со плоштината што ја зафаќа еден човек во однос на проценетата густина на посетеност на собирот, приближно ќе го добиеме бројот на присутни лица.
Ова значи и дека, ако некој направи одредена пресметка за бројноста на луѓето на еден собир, таа може да се провери дали е точна или не, едноставно ако се подели плоштината на вкупната површина со проценетиот број лица. Ако добиениот број не се совпаѓа со нашата проценка на густината, тогаш станува збор за погрешна пресметка (намерна или ненамерна).
Така на пример, за верскиот празник Водици во Охрид во 2016 година, коментаторот на телевизија соопшти дека на брегот на Езерото имало 20000 лица што го следеле овој настан. Дали оваа бројка е реална? Од снимките на дронот, но и од многуте слики направени од присутните, може да се види каде и на кој дел од брегот на Eзерото стојат луѓето. Очигледно е дека луѓето се густо распоредени на потегот од пристништето по улицата Коста Абраш, но не до крајот, туку само до таму од каде што може убаво да се види настанот. Со помош на Google Earth, пресметувајќи плоштина на различни полигони, може да се утврди дека плоштината на целото пристаниште и споменатиот дел од брегот изнесува околу 3600 квадратни метри. Според тоа, ако оваа квадратура ја поделиме со 0,42 (онолку место колку што зафаќа еден човек на густо посетен собир), ќе добиеме дека станува збор за 8570 лица.
Ова значи и дека, ако некој направи одредена пресметка за бројноста на луѓето на еден собир, таа може да се провери дали е точна или не, едноставно ако се подели плоштината на вкупната површина со проценетиот број лица. Ако добиениот број не се совпаѓа со нашата проценка на густината, тогаш станува збор за погрешна пресметка (намерна или ненамерна).
Така на пример, за верскиот празник Водици во Охрид во 2016 година, коментаторот на телевизија соопшти дека на брегот на Езерото имало 20000 лица што го следеле овој настан. Дали оваа бројка е реална? Од снимките на дронот, но и од многуте слики направени од присутните, може да се види каде и на кој дел од брегот на Eзерото стојат луѓето. Очигледно е дека луѓето се густо распоредени на потегот од пристништето по улицата Коста Абраш, но не до крајот, туку само до таму од каде што може убаво да се види настанот. Со помош на Google Earth, пресметувајќи плоштина на различни полигони, може да се утврди дека плоштината на целото пристаниште и споменатиот дел од брегот изнесува околу 3600 квадратни метри. Според тоа, ако оваа квадратура ја поделиме со 0,42 (онолку место колку што зафаќа еден човек на густо посетен собир), ќе добиеме дека станува збор за 8570 лица.
Собир на верниците за време на Водици во Охрид во 2016 год.
Но, ако сметаме дека луѓето се многу збиени еден до друг и ја искористиме бројката од 0,25 квадратни метри што може да ги зафаќа еден човек, тогаш би добиле бројка од 14400 лица. Веројатно вистината е некаде измеѓу.
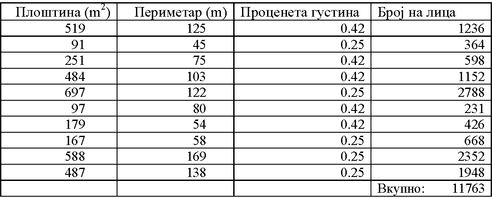
Може да се направи и попрацизна пресметка. Имено, од сликата се гледа дека луѓето некаде се погусто, а некаде поретко разместени, па ако ги искористиме податоците од Google Earth и нашата проценка на густината во секој од полигоните, би добиле една ваква табела:
Може да се направи и попрацизна пресметка. Имено, од сликата се гледа дека луѓето некаде се погусто, а некаде поретко разместени, па ако ги искористиме податоците од Google Earth и нашата проценка на густината во секој од полигоните, би добиле една ваква табела:
Ако сметаме дека сме направиле грешка од 10%, можеме да заклучиме дека настанот го следеле меѓу 10587 и 12939 лица или грубо, меѓу 10500 и 13000 лица. Според тоа, 20000 присутни на овој настан е преценета бројка. Оваа бројка би се постигнала, само ако на целата плоштината од 3560 квадратни метри, луѓето се рамномерно распоредени со густина од 5,6 луѓе на метар квадратен, односно 0,18 метри квадратни за еден човек, што воопшто не одговара на сликата од собирот.
Денес, компаниите како што е, на пример, Digital Design and Imaging Service, користат софистицирани методи за проценка на бројноста на масовни собири кои ја пресметуваат бројноста со грешка до најмногу 10%.
Денес, компаниите како што е, на пример, Digital Design and Imaging Service, користат софистицирани методи за проценка на бројноста на масовни собири кои ја пресметуваат бројноста со грешка до најмногу 10%.
Литература:
[1] Rob Goodier, The Curious Science of Counting a Crowd, www.popularmechanics.com/science/a7121/the-curious-science-of-counting-a-crowd/
[2] Ray Watson, Paul Yip, How many were there when it mattered? Estimating the sizes of crowds, Significance, Vol.8, Issue 3, 104–107, 2011
[3] Dr. Dirk Oberhagemann, Static and Dynamic Crowd Densities at Major Public Events, Technical Report TB 13 - 01, Technisch-Wissenschaftlicher Beirat (TWB), March 2012
[4] Prof. Dr. G. Keith Still, Crowd Safety and Risk Analysis, Static crowd density (general), http://www.gkstill.com/Support/crowd-density/CrowdDensity-1.html
[1] Rob Goodier, The Curious Science of Counting a Crowd, www.popularmechanics.com/science/a7121/the-curious-science-of-counting-a-crowd/
[2] Ray Watson, Paul Yip, How many were there when it mattered? Estimating the sizes of crowds, Significance, Vol.8, Issue 3, 104–107, 2011
[3] Dr. Dirk Oberhagemann, Static and Dynamic Crowd Densities at Major Public Events, Technical Report TB 13 - 01, Technisch-Wissenschaftlicher Beirat (TWB), March 2012
[4] Prof. Dr. G. Keith Still, Crowd Safety and Risk Analysis, Static crowd density (general), http://www.gkstill.com/Support/crowd-density/CrowdDensity-1.html
Автори:
Весна Целакоска-Јорданова, Институт за математика, Природно математички факултет, Скопје
Ирена Стојковска, Институт за математика, Природно математички факултет, Скопје
Објавено на ПОИМ:
18 јануари 2017
Начин на цитирање на статијата:
В. Целакоска-Јорданова, И Стојковска, Како се проценува бројот на луѓе на јавни собири, Портал ПОИМ на Институтот за математика, ПМФ, Скопје, 18 јануари 2017, http://poim-pmf.weebly.com/kako-se-procenuva-brojot-na-lugje-na-javni-sobiri.html
Весна Целакоска-Јорданова, Институт за математика, Природно математички факултет, Скопје
Ирена Стојковска, Институт за математика, Природно математички факултет, Скопје
Објавено на ПОИМ:
18 јануари 2017
Начин на цитирање на статијата:
В. Целакоска-Јорданова, И Стојковска, Како се проценува бројот на луѓе на јавни собири, Портал ПОИМ на Институтот за математика, ПМФ, Скопје, 18 јануари 2017, http://poim-pmf.weebly.com/kako-se-procenuva-brojot-na-lugje-na-javni-sobiri.html
Download (PDF)
Авторизираните статии објавени на Порталот подлежат на законска заштита. Се забранува користење на статиите без наведување на авторот или изворот.