НАУЧНО - ПОПУЛАРНИ СТАТИИСе залагаме за зголемување на свеста за местото и улогата на математиката во науките, технологијата, наставата, природата и културата.
|
Џон Форбс Неш (1923 – 2015): Пофалба на извондредниот ум
|
Прекрасниот ум на Џон Неш, славниот математичар од Универзитетот во Принстон и добитник на Нобеловата награда, згасна на 23 мај, 2015 година. Тој и неговата сопруга ги загубија своите животи во трагична сообраќајна несреќа, кога таксито со кое се враќале кон својот дом неконтролирано излегло од патот, удирајќи во заштитната ограда, а потоа во друг автомобил, со јачина од која двајцата патници излетале од возилото. Џон Неш имаше 86, а неговата сопруга Алиша 82 години.
Славата која Неш ја стекна уште во студентските денови се должи пред сé на неговиот придонес кон теоријата на игри за кој многу подоцна, во 1994 година, ја подели Нобеловата награда за економија со Рајнхард Селтен (Reinhard Selten) и Џон Харшањи (John Harsanyi). Фундаментален придонес даде и во областа на диференцијалната геометрија и парцијалните диференцијални равенки. Сепак, научниот придонес во игрите се издвојува по својот невообичаен апликативен потенцијал, опфаќајќи најразлични активности како што се секојдневните општествени интеракции, спорт, бизнис, политика, право, дипломатија, војна. Нешовиот придонес кон теоријата на игри извршил влијаниe во економијата, развојната биологија, вештачката интелигенција, компјутерските науки, теоретската физика, психологијата, воената теорија, социологијата... |
1. Биографски податоци
Џон Форбс Неш (John Forbes Nash Jr.) е роден во Блуфилд, Западна Вирџинија (САД) на 13 јуни 1928 година. Неговиот татко бил електроинженер, а мајка му учителка. Учел во државно училиште. Родителите постојано барале можности за надополнување на неговото образование, па така посетувал неколку напредни курсеви од различни области, меѓу кои хемија (која му била омилена) и математика. Добил стипендија за Карнеги институтот за технологија, каде што првично ја одбрал насоката хемискo инженерство. Подоцна се префрлил на хемија, за на крајот да се одлучи за математика. На Карнеги се заинтересирал за „преговарачкиот проблем“ кој останал нерешен во книгата на Џон вон Нојман, "The Theory of Games and Economic Behavior" (1928). Учествувал и во тамошната работна група за теорија на игри. По дипломирањето и магистратурата, во 1948 бил примен на Универзитетот во Харвард, но подоцна ја прифатил понудата од шефот на математичкиот оддел во Принстон, Соломон Лифшиц (Solomon Lefscheetz) и стипендијата за постдипломски студии на овој универзитет. Препораката која неговиот ментор Ричард Дафин (Richard Duffin) притоа ја напишал, се состоела од само една реченица: „Овој човек е генијалец.“ На Принстон тој ја започнува својата работа на теоријата на еквилибриум, која подоцна ќе стане позната под името Нешов еквилибиум.
Животот на Џон Неш беше одбележан и од неизвесната борба со менталната болест (параноидна шизофренија). По појавата на првите очигледни знаци (во 1959 година), Неш поминал неколку години во психијатриски установи, а некаде од 1970 неговата состојба полека се подобрила. Во средината на 1980-тите се враќа на академските активности. „Ова нарушување го имав многу долго време, околу 25 години“, - изјави Неш во интервјуто дадено во 2004 за Нобеловата веб страна (http://www.nobelprize.org/). Престојувал во болниците „секогаш недоброволно и секогаш со обиди за легално аргументиран отпуст“. Со текот на времето, тој престанал да ги зема лековите и се вратил на нормалните активности и истражувањето. Често изјавувал дека си го повратил здравјето едноставно отфрлајќи ги ирационалните мисли, иако сметал дека тие се изворот на неговата невообичаена инспирација и творештво.
Џон Форбс Неш (John Forbes Nash Jr.) е роден во Блуфилд, Западна Вирџинија (САД) на 13 јуни 1928 година. Неговиот татко бил електроинженер, а мајка му учителка. Учел во државно училиште. Родителите постојано барале можности за надополнување на неговото образование, па така посетувал неколку напредни курсеви од различни области, меѓу кои хемија (која му била омилена) и математика. Добил стипендија за Карнеги институтот за технологија, каде што првично ја одбрал насоката хемискo инженерство. Подоцна се префрлил на хемија, за на крајот да се одлучи за математика. На Карнеги се заинтересирал за „преговарачкиот проблем“ кој останал нерешен во книгата на Џон вон Нојман, "The Theory of Games and Economic Behavior" (1928). Учествувал и во тамошната работна група за теорија на игри. По дипломирањето и магистратурата, во 1948 бил примен на Универзитетот во Харвард, но подоцна ја прифатил понудата од шефот на математичкиот оддел во Принстон, Соломон Лифшиц (Solomon Lefscheetz) и стипендијата за постдипломски студии на овој универзитет. Препораката која неговиот ментор Ричард Дафин (Richard Duffin) притоа ја напишал, се состоела од само една реченица: „Овој човек е генијалец.“ На Принстон тој ја започнува својата работа на теоријата на еквилибриум, која подоцна ќе стане позната под името Нешов еквилибиум.
Животот на Џон Неш беше одбележан и од неизвесната борба со менталната болест (параноидна шизофренија). По појавата на првите очигледни знаци (во 1959 година), Неш поминал неколку години во психијатриски установи, а некаде од 1970 неговата состојба полека се подобрила. Во средината на 1980-тите се враќа на академските активности. „Ова нарушување го имав многу долго време, околу 25 години“, - изјави Неш во интервјуто дадено во 2004 за Нобеловата веб страна (http://www.nobelprize.org/). Престојувал во болниците „секогаш недоброволно и секогаш со обиди за легално аргументиран отпуст“. Со текот на времето, тој престанал да ги зема лековите и се вратил на нормалните активности и истражувањето. Често изјавувал дека си го повратил здравјето едноставно отфрлајќи ги ирационалните мисли, иако сметал дека тие се изворот на неговата невообичаена инспирација и творештво.
Во периодот од 1945 до 1996, има објавено 23 научни студии. Некои од останатите резултати ја опфаќаат реалната алгебарска геометрија [1], диференцијалната геометрија (Нешовата теорема за изометрично сместување на Риманови површини во Евклидски простор), теоријата на сингуларност, нелинеарните параболични диференцијални равенки. Во биографијата Прекрасниот ум, [2] чиј автор е Силвија Насар (Sylvia Nasar), се зборува за разочарувањето кое го доживеал откако разбрал дека италјанскиот математичар Енио де Гиорги (Ennio de Giorgi) го докажал Хилбертовиот деветнаесетти проблем (кој се однесува на елиптичните парцијални диференцијални равенки) само неколку месеци пред тој да го добие резултатот. Секој од нив применил различен пристап во доказот, а се сметало дека ако само едниот го решел проблемот, ќе го добиел Филдсовиот медал.
Подоцнежните активности во напредната теорија на игри го покажуваат истиот нестандарден пристап кон проблемите кој го имал и во младоста. Покрај другото, предложил и одредени хипотези за менталните болести. Размислувањето на неприфатлив начин го споредил со невклопеност во вообичаените општествени функции и „штрајкување“, посматрано од економско гледиште. Размислувал и за проблеми од еволутивната психологија, за вредноста на човечките разлики и потенцијалните придобивки од нестандардните улоги и однесување [3]. Сметал дека луѓето може да бидат контролирани и мотивирани преку парите до тој степен што ќе го загубат рационалниот однос кон нив. Притоа ги критикува групите на интерес кои промовираат квази-доктрини засновани на Кејнзијанската (John Maynard Keynes) економија каде што е дозволена манупулативна краткорочна инфлација и тактика на задолжување, којашто на крајот ја ослабува валутата. Предлагал глобален систем на „индустриски потрошувачки ценовен индекс“ кој ќе го поддржи развојот на „поидеални пари“ на кои луѓето ќе можат да им веруваат, наместо на нестабилните „лоши пари“. [4][5]
Во 2011 година, Националната агенција за безбедност (NSA) на САД ги обелодени писмата кои Неш ги напишал во 1950-те, во кои предлага нова машина за кодирање и декодирање. Овие писма покажуваат дека тој предвидел многу од концептите во модерната криптографија што се засновани на сметачката комплексност. [6]
2. Прекрасниот ум
Филмот Прекрасен ум (А Beautiful Mind, 2001) e снимен според истоимената биографија од 1998 на Силвија Насар. Тој е инспириран од академските достигнувања на научникот Џон Неш, но и од неговата борба со шизофренијата која безмалку му ги уништи кариерата и семејството. Филмот доби Оскар за најдобар филм, Џенифер Конели (Jennifer Connelly) како Алиша Неш го доби Оскарот за најдобра споредна женска улога, а Расел Кроу (Russell Crowe) во улогата на Џон Неш беше номиниран за најдобар актер. Неверојатно партнерство. Прекрасни умови, прекрасни срца, – се зборовите на Кроу по веста за несреќата.
Според Неш, оскаровскиот филм е своевидно уметничко видување на искуствата произлезени од менталната болест, кoja не ја опишува прецизно природата на неговите халуцинации. [7]
Подоцнежните активности во напредната теорија на игри го покажуваат истиот нестандарден пристап кон проблемите кој го имал и во младоста. Покрај другото, предложил и одредени хипотези за менталните болести. Размислувањето на неприфатлив начин го споредил со невклопеност во вообичаените општествени функции и „штрајкување“, посматрано од економско гледиште. Размислувал и за проблеми од еволутивната психологија, за вредноста на човечките разлики и потенцијалните придобивки од нестандардните улоги и однесување [3]. Сметал дека луѓето може да бидат контролирани и мотивирани преку парите до тој степен што ќе го загубат рационалниот однос кон нив. Притоа ги критикува групите на интерес кои промовираат квази-доктрини засновани на Кејнзијанската (John Maynard Keynes) економија каде што е дозволена манупулативна краткорочна инфлација и тактика на задолжување, којашто на крајот ја ослабува валутата. Предлагал глобален систем на „индустриски потрошувачки ценовен индекс“ кој ќе го поддржи развојот на „поидеални пари“ на кои луѓето ќе можат да им веруваат, наместо на нестабилните „лоши пари“. [4][5]
Во 2011 година, Националната агенција за безбедност (NSA) на САД ги обелодени писмата кои Неш ги напишал во 1950-те, во кои предлага нова машина за кодирање и декодирање. Овие писма покажуваат дека тој предвидел многу од концептите во модерната криптографија што се засновани на сметачката комплексност. [6]
2. Прекрасниот ум
Филмот Прекрасен ум (А Beautiful Mind, 2001) e снимен според истоимената биографија од 1998 на Силвија Насар. Тој е инспириран од академските достигнувања на научникот Џон Неш, но и од неговата борба со шизофренијата која безмалку му ги уништи кариерата и семејството. Филмот доби Оскар за најдобар филм, Џенифер Конели (Jennifer Connelly) како Алиша Неш го доби Оскарот за најдобра споредна женска улога, а Расел Кроу (Russell Crowe) во улогата на Џон Неш беше номиниран за најдобар актер. Неверојатно партнерство. Прекрасни умови, прекрасни срца, – се зборовите на Кроу по веста за несреќата.
Според Неш, оскаровскиот филм е своевидно уметничко видување на искуствата произлезени од менталната болест, кoja не ја опишува прецизно природата на неговите халуцинации. [7]
Прекрасен ум (А Beautiful Mind, 2001)
Настаните прикажани во филмот значително се разликуваат од вистинските, но неговите креатори тврдат дека воопшто немале намера да дадат точен приказ на Нешовиот живот. На пример, додека Неш се движел на релација помеѓу Принстонскиот универзитет и Масачусетскиот институт за технологија и бил ангажиран како консултант за корпорацијата RAND во Калифорнија, во филмот е прикажано дека работел за Министерството за одбрана во Пентагон. Се вели дека тој страда од шизофрени халуцинaции уште за време на студиите, но во реалноста тие се појавиле неколку години подоцна. Во филмот тој страда од визуелни халуцинации, додека вистинскиот Неш имал само звучни халуцинации. Додека филмскиот лик во 1994 вели „земам понови лекови“, тој всушност од 1970 година не користел никакви лекови. Исто така, не држел говор при доделувањето на Нобеловата награда ниту почесно предавање, најверојатно поради неговата нестабилност. Дискусиите за Нешовиот еквилибриум, пак, во филмот се во голема мера поедноставени.
Натаму, не се споменува дека освен синот кој го добил во бракот со Алиша, тој претходно имал уште еден син од врската со болничарката Еленор Стир (Eleanor Stier, 1921-2005). Што се однесува до ликовите во филмот, само мал дел од нив одговараат на вистински личности. Не се споменува ниту тоа дека Џон и Алиша се развеле во 1963 и иако живееле заедно од 1970, ја обновиле својата врска во 1990-тите и повторно се венчале во 2001. Сепак според авторката Силвија Насар, иако далеку од вистинските настани, наративот во филмот е верен на духот на Нешовата приказна [8]. Oбид за прецизно опишување на биографските моменти од животот на Џон Неш е направен во документарниот филм Брилјантно лудило (A Brilliant Madness, [9]).
3. Нешовиот Еквилибриум
Дисертацијата под наслов Некооперативни игри [10], напишана на 27 страници, Џон Неш ја поднел на Мaтематичкиот факултет во Принстон во мај 1950, еден месец пред својот 22 роденден. Во неа е претставен концептот за еквилибриум во некооперативните игри, кој подоцна ќе стане доминантен во економските анализи и предвидувања, но и во многу други области и аспекти од секојдневната пракса.
Најпрво, што е игра? Може да ја посматраме како процес на интерактивно делување, во кој одлуките и исходите за секој од учесниците (т.н. играчи) зависат од дејствата на сите останати учесници. Кога ја бираме својата акција (стратегија) во игра, мора да го имаме предвид она што го прават другите играчи. Но, исто така мора да имаме предвид дека и тие размислуваат за нашиот избор на стратегии, а и за она што го мислиме за нивното размислување итн. Ги анализираме и мотивите на противниците, нивните верувања, нивните способности, достапните информации... Ова создава една комплексна слика во која дејствувањето наликува на таинствена уметничка вештина. Сепак, многу од аспектите на стратегиите и нивниот избор може систематски да се истражуваат, а дисциплината која се бави со тоа се нарекува Tеорија на игри.
Нешовиот еквилибриум (НЕ) се однесува на конечни игри со n играчи претставени преку нивните множества од чисти стратегии и соодветни функции на добивка, дефинирани за секоја комбинација од чисти стратегии. Точката на еквилибриум е всушност решението на играта, а со неа е поврзана вредност – добивка која ја обезбедува секој од играчите. Клучниот Нешов резултат (од кој всушност и произлегува овој концепт), е доказот за постоење на барем една еквилибриумска точка во секоја ваква игра и претставува обопштување на постоечкиот концепт на решение во нула-сума игра со двајца играчи.
Накратко, НЕ е состојба (избор на стратегии) во која ниту еден од играчите нема интерес да ја промени својата стратегија. Причината е во тоа што доколку одбере друга стратегија при непроменети стратегии на другите играчи, ќе добие стриктно помала добивка од онаа која веќе ја обезбедил во НЕ. Ако играта има единствен НЕ, тогаш тој ќе биде усвоен, т.е. играчите ќе ги играат неговите стратегии. Притоа, потребните услови кои тоа ќе го гарантираат се следните:
- делувањето на играчите е целосно во насока на максимизирање на сопствените добивки;
- играчите се интелигентни, рационални и беспрекорни во изведувањето на акциите;
- постои општо знаење дека сите играчи ги исполнуваат наведените услови, вклучително и овој услов.
Натаму, не се споменува дека освен синот кој го добил во бракот со Алиша, тој претходно имал уште еден син од врската со болничарката Еленор Стир (Eleanor Stier, 1921-2005). Што се однесува до ликовите во филмот, само мал дел од нив одговараат на вистински личности. Не се споменува ниту тоа дека Џон и Алиша се развеле во 1963 и иако живееле заедно од 1970, ја обновиле својата врска во 1990-тите и повторно се венчале во 2001. Сепак според авторката Силвија Насар, иако далеку од вистинските настани, наративот во филмот е верен на духот на Нешовата приказна [8]. Oбид за прецизно опишување на биографските моменти од животот на Џон Неш е направен во документарниот филм Брилјантно лудило (A Brilliant Madness, [9]).
3. Нешовиот Еквилибриум
Дисертацијата под наслов Некооперативни игри [10], напишана на 27 страници, Џон Неш ја поднел на Мaтематичкиот факултет во Принстон во мај 1950, еден месец пред својот 22 роденден. Во неа е претставен концептот за еквилибриум во некооперативните игри, кој подоцна ќе стане доминантен во економските анализи и предвидувања, но и во многу други области и аспекти од секојдневната пракса.
Најпрво, што е игра? Може да ја посматраме како процес на интерактивно делување, во кој одлуките и исходите за секој од учесниците (т.н. играчи) зависат од дејствата на сите останати учесници. Кога ја бираме својата акција (стратегија) во игра, мора да го имаме предвид она што го прават другите играчи. Но, исто така мора да имаме предвид дека и тие размислуваат за нашиот избор на стратегии, а и за она што го мислиме за нивното размислување итн. Ги анализираме и мотивите на противниците, нивните верувања, нивните способности, достапните информации... Ова создава една комплексна слика во која дејствувањето наликува на таинствена уметничка вештина. Сепак, многу од аспектите на стратегиите и нивниот избор може систематски да се истражуваат, а дисциплината која се бави со тоа се нарекува Tеорија на игри.
Нешовиот еквилибриум (НЕ) се однесува на конечни игри со n играчи претставени преку нивните множества од чисти стратегии и соодветни функции на добивка, дефинирани за секоја комбинација од чисти стратегии. Точката на еквилибриум е всушност решението на играта, а со неа е поврзана вредност – добивка која ја обезбедува секој од играчите. Клучниот Нешов резултат (од кој всушност и произлегува овој концепт), е доказот за постоење на барем една еквилибриумска точка во секоја ваква игра и претставува обопштување на постоечкиот концепт на решение во нула-сума игра со двајца играчи.
Накратко, НЕ е состојба (избор на стратегии) во која ниту еден од играчите нема интерес да ја промени својата стратегија. Причината е во тоа што доколку одбере друга стратегија при непроменети стратегии на другите играчи, ќе добие стриктно помала добивка од онаа која веќе ја обезбедил во НЕ. Ако играта има единствен НЕ, тогаш тој ќе биде усвоен, т.е. играчите ќе ги играат неговите стратегии. Притоа, потребните услови кои тоа ќе го гарантираат се следните:
- делувањето на играчите е целосно во насока на максимизирање на сопствените добивки;
- играчите се интелигентни, рационални и беспрекорни во изведувањето на акциите;
- постои општо знаење дека сите играчи ги исполнуваат наведените услови, вклучително и овој услов.
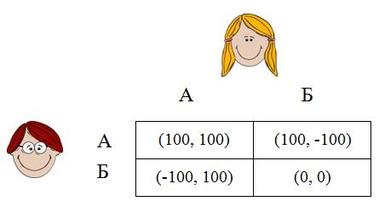
Ќе илустрираме еден очигледен пример на НЕ. Играчите (ќе ги викаме Тина и Томе) имаат по две стратегии А и Б, со чие играње може да добијат 100 денари, да загубат 100 денари или пак да останат со непроменета добивка. Притоа, ако и двајцата ја одберат стартегијата А ќе добијат по 100 денари, ако одберат Б кога другиот избрал А ќе загубат 100 денари, а ако и двајцата ја одберат Б тогаш ниту добиваат ниту губат. Оваа ситуација може да се прикаже во вид на (би)матрица (види слика). Па, ако и Тина и Томе го знаат ова, тогаш немаат никаква причина да отстапат од стратегијата А. Следствено, исходот (А,А) овде ќе биде (единствениот) НЕ. Секако, во повеќето случаи, дури и во едноставните игри со двајца играчи и две стратегии (т.н. 2х2 игри), ситуацијата не е вака очигледна и бара дополнителни анализи.
Условите кои овозможуваат еквилибриумска игра се доста ограничувачки, бидејќи наметнуваат високи барања чие исполнување во реалноста е малку веројатно. Друг проблем е што еквилибриумот е најчесто во вид на мешана стратегија, т.е. распределба од веројатности над множеството од чисти стратегии (акции). Ова го наметнува прашањето, како ќе се прави избор на идеалната стратегија при одреден потег и какво ќе биде нејзиното значење? Дополнителен проблем пак, настанува кај игрите кои имаат повеќе од еден НЕ, бидејќи тогаш се јавува потребата за избор помеѓу нив, т.н. координација на еквилибриум. Овие и многу други прашања кои произлегуваат од анализите на практичните ситуации, се теми кои се разгледуваат во различни подобласти од теоријата на игри.
4. Последните денови ...
Набргу по доаѓањето на Алберт Ајнштајн во Принстон во 1950-тите, Неш се сретнал со него при што му зборувал за своите идеи околу гравитацијата. Откако повеќе од еден час му објаснувал сложени математички теории, Ајнштајн го посоветувал да научи нешто повеќе за физиката. Но, се чини дека физичарот објавил слични идеи неколку години подоцна. Интересот за општата теорија на релативност не го напуштила Неш до крајот на животот. Само неколку денови пред смртта, тој му објаснувал на францускиот математичар Седрик Вилани (Cédric Villani) дека се наоѓа на работ на големо откритие во врска со Ајнштајновата теорија. Се обидувал да воведе нова мера на закривеност на просторот и времето, односно на промените на просторно-временските димензии во присуство на енергија. Вилани изјави за The Times: Сметаше дека открил замена за равенката. Оваа замена, сметал Неш, ќе овозможела дополнително објаснување на квантната гравитација.
Несреќата во која Џон и Алиша Неш трагично ги завршија своите животи, се случи при нивното враќање од Норвешка каде Џон ја прими Абеловата награда за математика за 2015 година, заедно со Луис Ниренберг (Louis Nirenberg) од Универзитетот Њу Јорк. Со неа му беше оддадено признание за неговиот придонес кон теоријата на парцијалните диференцијални равенки. Професорот Ниренберг изјави: Пред околу 20 години, кога некој ме праша, „Дали постојат математичари кои ги сметате за генијални?“, одговорив, „Можам да се сетам на еден, а тоа е Џон Неш.“ Тој имаше извонреден ум. Размислуваше за нештата поинаку од другите луѓе.
Извори:
[1] Nash, John Forbes (1952). "Real algebraic manifolds". Annals of Mathematics 56 (3): 405–21. doi:10.2307/1969649. JSTOR 1969649. MR 0050928.
[2] Nasar, Sylvia (1998). A Beautiful Mind. Simon & Schuster. ISBN 0-684-81906-6.
[3] Neubauer, David (June 1, 2007). "John Nash and a Beautiful Mind on Strike"
[4] Zuckerman, Julia (April 27, 2005) "Nobel winner Nash critiques economic theory", The Brown Daily Herald
[5] Nash, John (2002). "Ideal Money". Southern Economic Journal 69 (1): 411.doi:10.2307/1061553. JSTOR 1061553
[6] "John Nash's Letter to the NSA ; Turing's Invisible Hand"
[7] http://www.nobelprize.org/mediaplayer/index.php?id=429 (видео материјал)
[8] "A Real Number", Slate Magazine, 2001
[9] А Brilliant Madness
[10] Nash, John Forbes (1950), "Non-Cooperative Games" (PDF), PhD thesis, Princeton University
Автор:
Невена Серафимова, Воена академија „Генерал Михаило Апостолски“, Скопје
Објавено на ПОИМ:
12 јуни 2015
Начин на цитирање на статијата:
Н. Серафимова, Џон Форбс Неш (1923 - 2015): Пофалба на извондредниот ум, Портал ПОИМ на Институтот за математика, ПМФ, Скопје, 12 јуни 2015, http://poim-pmf.weebly.com/john-nash.html
Условите кои овозможуваат еквилибриумска игра се доста ограничувачки, бидејќи наметнуваат високи барања чие исполнување во реалноста е малку веројатно. Друг проблем е што еквилибриумот е најчесто во вид на мешана стратегија, т.е. распределба од веројатности над множеството од чисти стратегии (акции). Ова го наметнува прашањето, како ќе се прави избор на идеалната стратегија при одреден потег и какво ќе биде нејзиното значење? Дополнителен проблем пак, настанува кај игрите кои имаат повеќе од еден НЕ, бидејќи тогаш се јавува потребата за избор помеѓу нив, т.н. координација на еквилибриум. Овие и многу други прашања кои произлегуваат од анализите на практичните ситуации, се теми кои се разгледуваат во различни подобласти од теоријата на игри.
4. Последните денови ...
Набргу по доаѓањето на Алберт Ајнштајн во Принстон во 1950-тите, Неш се сретнал со него при што му зборувал за своите идеи околу гравитацијата. Откако повеќе од еден час му објаснувал сложени математички теории, Ајнштајн го посоветувал да научи нешто повеќе за физиката. Но, се чини дека физичарот објавил слични идеи неколку години подоцна. Интересот за општата теорија на релативност не го напуштила Неш до крајот на животот. Само неколку денови пред смртта, тој му објаснувал на францускиот математичар Седрик Вилани (Cédric Villani) дека се наоѓа на работ на големо откритие во врска со Ајнштајновата теорија. Се обидувал да воведе нова мера на закривеност на просторот и времето, односно на промените на просторно-временските димензии во присуство на енергија. Вилани изјави за The Times: Сметаше дека открил замена за равенката. Оваа замена, сметал Неш, ќе овозможела дополнително објаснување на квантната гравитација.
Несреќата во која Џон и Алиша Неш трагично ги завршија своите животи, се случи при нивното враќање од Норвешка каде Џон ја прими Абеловата награда за математика за 2015 година, заедно со Луис Ниренберг (Louis Nirenberg) од Универзитетот Њу Јорк. Со неа му беше оддадено признание за неговиот придонес кон теоријата на парцијалните диференцијални равенки. Професорот Ниренберг изјави: Пред околу 20 години, кога некој ме праша, „Дали постојат математичари кои ги сметате за генијални?“, одговорив, „Можам да се сетам на еден, а тоа е Џон Неш.“ Тој имаше извонреден ум. Размислуваше за нештата поинаку од другите луѓе.
Извори:
[1] Nash, John Forbes (1952). "Real algebraic manifolds". Annals of Mathematics 56 (3): 405–21. doi:10.2307/1969649. JSTOR 1969649. MR 0050928.
[2] Nasar, Sylvia (1998). A Beautiful Mind. Simon & Schuster. ISBN 0-684-81906-6.
[3] Neubauer, David (June 1, 2007). "John Nash and a Beautiful Mind on Strike"
[4] Zuckerman, Julia (April 27, 2005) "Nobel winner Nash critiques economic theory", The Brown Daily Herald
[5] Nash, John (2002). "Ideal Money". Southern Economic Journal 69 (1): 411.doi:10.2307/1061553. JSTOR 1061553
[6] "John Nash's Letter to the NSA ; Turing's Invisible Hand"
[7] http://www.nobelprize.org/mediaplayer/index.php?id=429 (видео материјал)
[8] "A Real Number", Slate Magazine, 2001
[9] А Brilliant Madness
[10] Nash, John Forbes (1950), "Non-Cooperative Games" (PDF), PhD thesis, Princeton University
Автор:
Невена Серафимова, Воена академија „Генерал Михаило Апостолски“, Скопје
Објавено на ПОИМ:
12 јуни 2015
Начин на цитирање на статијата:
Н. Серафимова, Џон Форбс Неш (1923 - 2015): Пофалба на извондредниот ум, Портал ПОИМ на Институтот за математика, ПМФ, Скопје, 12 јуни 2015, http://poim-pmf.weebly.com/john-nash.html
Download (PDF)
Авторизираните статии објавени на Порталот подлежат на законска заштита. Се забранува користење на статиите без наведување на авторот или изворот.