НАУЧНО - ПОПУЛАРНИ СТАТИИСе залагаме за зголемување на свеста за местото и улогата на математиката во науките, технологијата, наставата, природата и културата.
|
Мистеријата за датумот на Велигден
|
Од симетричноста на верските симболи до архитектурата на верските објекти, сликовито е прикажана примената на математиката во религијата. Точноста на одредувањето на деновите на верските обреди и правилата за нивно пресметување кои ги налагаат религиите, укажуваат на тоа дека математика отсекогаш имала голем удел во религиите.
|
Секоја година, според православниот верски календар, верските празници кои ги празнуваат православните христијани паѓаат на истите датуми. Но, не сите верски празници. На пример, што се случува со Велигден? Во христијанството познат како еден од најзначајните денови во годината, Велигден секоја година се одбележува во недела, но на различен датум. Како поточно се определува тој датум? Објаснувањето лежи во малку историја, астрономија, и секако – во изобилство од математички пресметки.
1. Историјата за празнувањето на Велигден
И покрај тоа што во многу земји низ светот Божиќните празници добиваат поголемо внимание, Велигден има поголемо религиско значење во христијанството. Одбележувањето на распнувањето на Исус Христос (Велики петок) и неговото воскресение (Велигден), претставува признавање на една од главните мистерии и ветувања на оваа религија: простување на гревовите и вечен живот.
1. Историјата за празнувањето на Велигден
И покрај тоа што во многу земји низ светот Божиќните празници добиваат поголемо внимание, Велигден има поголемо религиско значење во христијанството. Одбележувањето на распнувањето на Исус Христос (Велики петок) и неговото воскресение (Велигден), претставува признавање на една од главните мистерии и ветувања на оваа религија: простување на гревовите и вечен живот.
Токму поради големата важност на овој ден, Христијанската црква се стремела кон тоа да ги запази сите историски податоци од различните посланија. До средината на вториот век, се јавил проблемот за конкретниот датум на кој треба да се прославува Велигден. Христијаните се поделиле на две групи кои се одлучиле за различни датуми, според календарот што тогаш се користел. Едната група ја формирале Евреите кои го примиле христијанството како религија, а другата група ја формирале римските и александриските христијани. Првата група со текот на времето се распаднала, па се зголемила желбата на христијаните да се одделат од зависноста од еврејските авторитети, за да се избере еден датум за Велигден. Христијанската црква, во 325 година го донела следново правило: Неделата на Велигден, годишнината од воскресението, треба да се слави на првата недела после паскаловата полна месечина која доаѓа точно или по рамноденица, а паскаловата полна месечина се зема да биде точно на 14-тиот ден од паскаловата млада месечина. И покрај ова правило, проблемите за наоѓањето на точниот датум продолжиле. Римјаните сметале дека рамноденица е на 25 март, а Александријците го користеле 21 март.
2. Пресметување на датумот на Велигден според Јулијанскиот календар
Низ историјата сметањето на времето претрпело различни промени. Со ширењето на христијанството се донеле и нови, астрономски приспособени календари. На почетокот, Римјаните го користеле календарот AUC – Ab Urbe Condita или „од основањето на Рим“. Овој календар не бил адекватен за развивањето на Римската империја, па во 45 век п.н.е., (што е 709 AUC), римскиот император Јулие Цезар ги прифатил предлозите на астрономите и го присвоил подоцна наречениот Јулијански календар. Јулијанскиот календар во една година броел 365 дена и секоја четврта (престапна) година добивала по еден ден повеќе, т.е. 366. Јулијанската соларна година била долга 365,25 дена.
Традиционалните начини за наоѓање на датумот на Велигден, вклучуваат: табели за месечеви циклуси, златни броеви, паскалова полна месечина и соодветна буква/број за секој ден од неделата. За пресметување на датумот на Велигден без користење табели, воведен е поимот епакт. Во продолжение ќе ги објасниме поимите потребни за пресметување на точниот датум.
Месечевиот циклус познат како метонски циклус е долг 19 години. Под златен број (G) го подразбираме бројот што ја укажува позицијата на некоја конкретна година во метонскиот циклус. Златниот број варира помеѓу 1 и 19. Првата година пред новата ера се смета како прва година од метонскиот циклус, па златниот број G се пресметува со формулата:
2. Пресметување на датумот на Велигден според Јулијанскиот календар
Низ историјата сметањето на времето претрпело различни промени. Со ширењето на христијанството се донеле и нови, астрономски приспособени календари. На почетокот, Римјаните го користеле календарот AUC – Ab Urbe Condita или „од основањето на Рим“. Овој календар не бил адекватен за развивањето на Римската империја, па во 45 век п.н.е., (што е 709 AUC), римскиот император Јулие Цезар ги прифатил предлозите на астрономите и го присвоил подоцна наречениот Јулијански календар. Јулијанскиот календар во една година броел 365 дена и секоја четврта (престапна) година добивала по еден ден повеќе, т.е. 366. Јулијанската соларна година била долга 365,25 дена.
Традиционалните начини за наоѓање на датумот на Велигден, вклучуваат: табели за месечеви циклуси, златни броеви, паскалова полна месечина и соодветна буква/број за секој ден од неделата. За пресметување на датумот на Велигден без користење табели, воведен е поимот епакт. Во продолжение ќе ги објасниме поимите потребни за пресметување на точниот датум.
Месечевиот циклус познат како метонски циклус е долг 19 години. Под златен број (G) го подразбираме бројот што ја укажува позицијата на некоја конкретна година во метонскиот циклус. Златниот број варира помеѓу 1 и 19. Првата година пред новата ера се смета како прва година од метонскиот циклус, па златниот број G се пресметува со формулата:
G = 1 + mod (Y, 19),
каде што Y е конкретната година од новата ера. Изразот mod (Y, 19) го означува остатокот при делење на Y со 19.
Пример 1.
Ако Y = 2015, остатокот при делење на 2015 со 19 е 1, па златниот број на 2015 година е G = 1 + mod (2015, 19) = 1 + 1 = 2. Значи, оваа 2015 година од новата ера е 2-ра година во метонскиот циклус.
Паскалова полна месечина е првата полна месечина која се случува на или по рамнодневица, којашто традиционално се зема да биде 21 март. Полна месечина настанува 14 дена по соодветната млада месечина, што се зема како прв ден. Значи, паскаловата нова месечина се случува порано од 13 дена пред 21 март. Паскаловата млада месечина варира помеѓу 8 март и 5 април, додека паскаловата полна месечина е помеѓу 21 март и 18 април.
Земајќи ги предвид овие датуми на паскалова полна месечина, можеме да побараме каде варира датумот на Велигден. Ако на 21 март има полна месечина, најблиската можна недела по 21 март би била 22 март. Ако на 18 април има полна месечина и е недела, Велигден би дошол на 25 април, но никако подоцна. Значи, неделата на Велигден може да биде на кој било датум помеѓу 22 март и 25 април според Јулијанскиот календар.
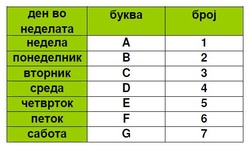
Бидејќи Велигден се слави во недела, мора да постои начин да се најде точниот ден на кој доаѓа некој датум. За оваа цел се задаваат букви/броеви на деновите во неделата. Седум букви A – G или броевите од 1 до 7 се задаваат на деновите од неделата (види Слика 1). Така, буквата А се задава на првиот ден во годината – први јануари, па останатите продолжуваат редоследно во циклус. 8 јануари ја добива повторно буквата А, на 9 јануари одговара B и т.н. Во престапни години, 29 февруари ја добива истата буква како и 1 март. Овие букви се викаат „календарски букви“ и главно се користат во табеларни пресметувања.
Пример 1.
Ако Y = 2015, остатокот при делење на 2015 со 19 е 1, па златниот број на 2015 година е G = 1 + mod (2015, 19) = 1 + 1 = 2. Значи, оваа 2015 година од новата ера е 2-ра година во метонскиот циклус.
Паскалова полна месечина е првата полна месечина која се случува на или по рамнодневица, којашто традиционално се зема да биде 21 март. Полна месечина настанува 14 дена по соодветната млада месечина, што се зема како прв ден. Значи, паскаловата нова месечина се случува порано од 13 дена пред 21 март. Паскаловата млада месечина варира помеѓу 8 март и 5 април, додека паскаловата полна месечина е помеѓу 21 март и 18 април.
Земајќи ги предвид овие датуми на паскалова полна месечина, можеме да побараме каде варира датумот на Велигден. Ако на 21 март има полна месечина, најблиската можна недела по 21 март би била 22 март. Ако на 18 април има полна месечина и е недела, Велигден би дошол на 25 април, но никако подоцна. Значи, неделата на Велигден може да биде на кој било датум помеѓу 22 март и 25 април според Јулијанскиот календар.
Бидејќи Велигден се слави во недела, мора да постои начин да се најде точниот ден на кој доаѓа некој датум. За оваа цел се задаваат букви/броеви на деновите во неделата. Седум букви A – G или броевите од 1 до 7 се задаваат на деновите од неделата (види Слика 1). Така, буквата А се задава на првиот ден во годината – први јануари, па останатите продолжуваат редоследно во циклус. 8 јануари ја добива повторно буквата А, на 9 јануари одговара B и т.н. Во престапни години, 29 февруари ја добива истата буква како и 1 март. Овие букви се викаат „календарски букви“ и главно се користат во табеларни пресметувања.
Слика1. Календарски букви и броеви потребни за традиционалниот начин на пресметување на датумот на Велигден
Главната формула за пресметување на календарскиот број C (број кој одговара на календарската буква) е C = mod (F + D – 1, 7), каде што F ни го претставува календарскиот број на првиот ден од месецот, D е денот во месецот, а C ни го дава календарскиот број на датумот кој го бараме. Со оваа формула добиваме броеви од 0 до 6. За да го приспособиме овој опсег да биде од 1 до 7, формулата добива едно „-1“ во аргументот на конгруенцијата, и „+1“ надвор. За упростување на формулата, со R го означуваме денот во март, па R = F + D. Календарскиот број го добиваме со формулата:
C = 1 + mod (R – 2, 7)
Да се вратиме на редните календарски броеви/букви на деновите. Распоредот на овие броеви/букви се менува во текот на годините, поради две причини:
Прво, секоја соларна година има 52 недели и 1 ден, последниот и првиот ден во годината би имале иста соодветна буква/број. Одовде следува дека во следната година овие букви ќе се „поместат“ за една, односно понеделник ја добива буквата А наместо B, вторник - B наместо C, и така натаму, недела - G наместо А. Ова поместување за едно место на назад, е познато како регресија.
Второ, престапната година добива уште еден ден, 29 февруари, па календарските букви ќе се поместат уште еднаш. Со ова поместување, гледаме дека годината која доаѓа по престапна година има регресија 2.
Календарската буква/број на денот во неделата е строго поврзана со бројот на регресии кои се случиле пред годината која е во прашање. Можеме да го пресметамекалендарскиот број N во некоја година Y со помош на бројот на регресии Г до крајот на годината Y. Овде се зема предвид престапната година во Јулијанскиот календар.
Бројот на регресии Г до крајот на годината Y, почнувајќи од 1 година од новата ера е Y – 1. Првата година од новата ера има 0 регресии. Во продолжение, во периодот помеѓу првата година и Y, има [Y/4] регресии, каде што изразот [Y/4] означува цел дел од бројот што се добива при делење на годината Y со 4. Значи, до крајот на годината Y вкупниот број на регресии е
Прво, секоја соларна година има 52 недели и 1 ден, последниот и првиот ден во годината би имале иста соодветна буква/број. Одовде следува дека во следната година овие букви ќе се „поместат“ за една, односно понеделник ја добива буквата А наместо B, вторник - B наместо C, и така натаму, недела - G наместо А. Ова поместување за едно место на назад, е познато како регресија.
Второ, престапната година добива уште еден ден, 29 февруари, па календарските букви ќе се поместат уште еднаш. Со ова поместување, гледаме дека годината која доаѓа по престапна година има регресија 2.
Календарската буква/број на денот во неделата е строго поврзана со бројот на регресии кои се случиле пред годината која е во прашање. Можеме да го пресметамекалендарскиот број N во некоја година Y со помош на бројот на регресии Г до крајот на годината Y. Овде се зема предвид престапната година во Јулијанскиот календар.
Бројот на регресии Г до крајот на годината Y, почнувајќи од 1 година од новата ера е Y – 1. Првата година од новата ера има 0 регресии. Во продолжение, во периодот помеѓу првата година и Y, има [Y/4] регресии, каде што изразот [Y/4] означува цел дел од бројот што се добива при делење на годината Y со 4. Значи, до крајот на годината Y вкупниот број на регресии е
Г = Y – 1 + [Y / 4]
Први јануари во првата година од новата ера бил во сабота. Ова значи дека календарската буква на недела во првата година од новата ера била B, и календарскиот број 2. Значи, кога mod (Г, 7) = 0, календарскиот број на недела е N = 2; кога mod (Г, 7) = 1, календарскиот број на недела ќе се врати за 1, па N = 1; а кога mod (Г, 7) = 2, календарскиот број на недела ќе се врати повторно за 1, па N = 7. Одовде добиваме:
N = 7 – mod (Г – 2, 7)
Ако овде го замениме претходно добиениот израз за регресија, имаме:
N = 7 - mod (Y – 1 + [Y / 4] – 2, 7) = 7 - mod (Y – 3 + [Y / 4], 7) = 7 - mod (Y + 4 + [Y / 4], 7)
Пример 1. (продолжува)
Календарскиот број на денот недела оваа 2015 година е:
N = 7 – mod (2015 + 4 + [2015/4], 7) = 7 – mod (2019 + 503, 7) = 7 – mod ( 2522, 7) = 7 – 2 = 5
Значи редниот календарски број на денот недела оваа 2015 година е 5, а соодветната буква е Е.
Користејќи го знаењето за определување на календарската буква или редниот број на денот во неделата, можеме лесно да го определиме денот од неделата W на кој ќе биде некој конкретен датум. Нека C е календарскиот реден број на избраниот датум, и N календарскиот реден број на денот недела. Ако C – N = 0, нашиот избран датум очигледно е недела. По оваа логика, ако C – N = 1, се работи за понеделник, ако C – N = 2, тоа е вторник и т.н. За да ги избегнеме негативните вредности за W, формулата ја поставуваме на следниов начин:
Календарскиот број на денот недела оваа 2015 година е:
N = 7 – mod (2015 + 4 + [2015/4], 7) = 7 – mod (2019 + 503, 7) = 7 – mod ( 2522, 7) = 7 – 2 = 5
Значи редниот календарски број на денот недела оваа 2015 година е 5, а соодветната буква е Е.
Користејќи го знаењето за определување на календарската буква или редниот број на денот во неделата, можеме лесно да го определиме денот од неделата W на кој ќе биде некој конкретен датум. Нека C е календарскиот реден број на избраниот датум, и N календарскиот реден број на денот недела. Ако C – N = 0, нашиот избран датум очигледно е недела. По оваа логика, ако C – N = 1, се работи за понеделник, ако C – N = 2, тоа е вторник и т.н. За да ги избегнеме негативните вредности за W, формулата ја поставуваме на следниов начин:
W = 1 + mod (C – n + 7, 7)
Конечно, дојдовме до терминот епакт. Имено, под епакт (Е) на една година, ја подразбираме староста на месечината, во денови, на 1 јануари во годината. Доколку на 1 јануари имаме млада месечина, таа година има епакт 0. За пресметување на Јулијанскиот епакт, се користи претходно воведениот поим за златен број, G. Така, Јулијанскиот епакт се пресметува според следнава формула:
E = mod (11 • (G – 3), 30)
Една карактеристика на епактот е дека во секоја следна година, тој се зголемува за 11. Оваа карактеристика следува од фактот дека една месечева година (354 дена) е за 11 дена пократка од соларната година (365 дена). Бидејќи еден лунарен циклус не надминува 30 дена, вредноста на епактот никогаш не е поголема од 30, што ни ја дава вредноста на модулот во формулата.
На Слика 2 шематски е прикажан алгоритмот за пресметување на точниот датум на Велигден според Јулијанскиот календар, за некоја конкретна година Y.
На Слика 2 шематски е прикажан алгоритмот за пресметување на точниот датум на Велигден според Јулијанскиот календар, за некоја конкретна година Y.
Слика2. Алгоритам за пресметување на точниот датум на Велигден според Јулијанскиот календар
Пример 1. (продолжува)
Да го употребиме овој алгоритам за да го пресметаме датумот на кој Велигден се славеше оваа, 2015 година.
Y = 2015
G = 1 + mod (2015, 19) = 1 + 1 = 2
E = mod (11 (2 – 3), 30) = mod (11 (-1), 30) = mod (-11, 30) = mod (19, 30) = 19
R = 21 + mod (54 – 19, 30) = 21 + mod (35, 30) = 21 + 5 = 26
C = 1 + mod (26 + 2, 7) = 1 + mod (28, 7) = 1
N = 7 – mod (2015 + 4 + [2015 / 4], 7) = 7 – mod (2019 + 503, 7) = 7 – mod (2522, 7) = 7 – 2 = 5
S = 26 + 7 – mod (1 – 5, 7) = 33 – 3 =30
Значи, според Јулијанскиот календар, оваа година Велигден беше на 30-тиот ден од Март.
3. Префрлање на датумот од Јулијански во Грегоријански календар
Иако долги години Јулијанскиот календар се користел од страна на Римската империја, и од таму – христијанската црква, со текот на времето, грешката која ја давало пресметувањето во однос на овој календар излегла на виделина. Должината на една година во Јулијанскиот календар е 365,25 дена, а должината на една астрономна тропска година е долга приближно 365,2422 дена. Значи Јулијанската година е подолга од вистинската должина на една година за 0,0078 дена, или тоа е приближно 11 минути. Оваа грешка се акумулирала со текот на времето, па до 1582 година, рамноденицата се случувала на 11 март, цели 10 дена пред денот кога се очекувала – 21 март.
Доколку оваа грешка продолжела да се занемарува, Велигден би требало да се слави во лето, а со текот на времето дури и во зима. Овие промени не биле прифатливи од страна на Римо-Католичката црква, бидејќи Велигден се сметал за еден од најважните денови во годината за христијанската вера. Папата Грегориј III, (римски папа од 18 март 731, до неговата смрт на 29 ноември 741) наредил да се направат соодветни реформи на Јулијанскиот календар. Новиот календар, заедно со сите реформи ја запазува точноста и вистинската должина на годината. Познат е под името Грегоријански календар, според папата Грегори III, и тоа е календарот кој и денес се користи секаде во светот.
Православната црква не ги прифатила овие промени, па православниот Велигден се пресметува на погоре прикажаниот начин. Бидејќи датумот на кој православните христијани го слават Велигден, треба сепак да се прилагоди на Грегоријанскиот календар, на крај на пресметките добиениот датум се „поместува“ за онолку дена колкава што е грешката на Јулијанскиот календар, акумулирана се до соодветната година. Така,до оваа, 2015 година, грешката нараснала на 13 дена, а на 28 февруари 2100 година по Грегоријански календар, истата ќе достигне 14 дена.
Пример 1. (продолжува)
Да се вратиме на нашиот пример. Оваа година, според Јулијанскиот календар, добивме дека Велигден беше на 30 март. Нам ни е потребен овој ден, но пресметан во Грегоријански календар. Бидејќи грешката меѓу овие два календара сé до 2100 година е со големина од 13 дена, овој датум треба да го поместиме за 13 дена нанапред. Значи, 30 + 13 = 43, т.е. оваа 2015 година Велигден ќе биде на 43-тиот ден од март, односно на 43 - 31 = 12 април.
Сега, да го пресметаме датумот на кој Велигден ќе се слави следната 2016 година..
Y = 2016
G = 1 + mod (2016, 19) = 1 + 2 = 3
E = mod (11 (3 – 3), 30) = 0
R = 21 + mod (54 – 0, 30) = 21 + 24 = 45
C = 1 + mod (45 + 2, 7) = 1 + mod (47, 7) = 1 + 5 = 6
N = 7 – mod (2016 + 4 + [2016 / 4], 7) = 7 – mod (2020 + 504, 7) = 7 – 4 = 3
S = 45 + 7 – mod (6 – 3, 7) = 52 – 3 = 49
Значи, според Јулијанскиот календар, следната 2016 година Велигден ќе биде на 49-тиот ден од Март, односно 49 – 31 = 18 април. Додека, според Грегоријанскиот календар, тоа ќе биде на 18 + 13 = 31-виот ден од април, што одговара на 1-ви мај.
На Слика 3 е дадена табела со точните датуми на православниот Велигден, во текот на 30 години.
Да го употребиме овој алгоритам за да го пресметаме датумот на кој Велигден се славеше оваа, 2015 година.
Y = 2015
G = 1 + mod (2015, 19) = 1 + 1 = 2
E = mod (11 (2 – 3), 30) = mod (11 (-1), 30) = mod (-11, 30) = mod (19, 30) = 19
R = 21 + mod (54 – 19, 30) = 21 + mod (35, 30) = 21 + 5 = 26
C = 1 + mod (26 + 2, 7) = 1 + mod (28, 7) = 1
N = 7 – mod (2015 + 4 + [2015 / 4], 7) = 7 – mod (2019 + 503, 7) = 7 – mod (2522, 7) = 7 – 2 = 5
S = 26 + 7 – mod (1 – 5, 7) = 33 – 3 =30
Значи, според Јулијанскиот календар, оваа година Велигден беше на 30-тиот ден од Март.
3. Префрлање на датумот од Јулијански во Грегоријански календар
Иако долги години Јулијанскиот календар се користел од страна на Римската империја, и од таму – христијанската црква, со текот на времето, грешката која ја давало пресметувањето во однос на овој календар излегла на виделина. Должината на една година во Јулијанскиот календар е 365,25 дена, а должината на една астрономна тропска година е долга приближно 365,2422 дена. Значи Јулијанската година е подолга од вистинската должина на една година за 0,0078 дена, или тоа е приближно 11 минути. Оваа грешка се акумулирала со текот на времето, па до 1582 година, рамноденицата се случувала на 11 март, цели 10 дена пред денот кога се очекувала – 21 март.
Доколку оваа грешка продолжела да се занемарува, Велигден би требало да се слави во лето, а со текот на времето дури и во зима. Овие промени не биле прифатливи од страна на Римо-Католичката црква, бидејќи Велигден се сметал за еден од најважните денови во годината за христијанската вера. Папата Грегориј III, (римски папа од 18 март 731, до неговата смрт на 29 ноември 741) наредил да се направат соодветни реформи на Јулијанскиот календар. Новиот календар, заедно со сите реформи ја запазува точноста и вистинската должина на годината. Познат е под името Грегоријански календар, според папата Грегори III, и тоа е календарот кој и денес се користи секаде во светот.
Православната црква не ги прифатила овие промени, па православниот Велигден се пресметува на погоре прикажаниот начин. Бидејќи датумот на кој православните христијани го слават Велигден, треба сепак да се прилагоди на Грегоријанскиот календар, на крај на пресметките добиениот датум се „поместува“ за онолку дена колкава што е грешката на Јулијанскиот календар, акумулирана се до соодветната година. Така,до оваа, 2015 година, грешката нараснала на 13 дена, а на 28 февруари 2100 година по Грегоријански календар, истата ќе достигне 14 дена.
Пример 1. (продолжува)
Да се вратиме на нашиот пример. Оваа година, според Јулијанскиот календар, добивме дека Велигден беше на 30 март. Нам ни е потребен овој ден, но пресметан во Грегоријански календар. Бидејќи грешката меѓу овие два календара сé до 2100 година е со големина од 13 дена, овој датум треба да го поместиме за 13 дена нанапред. Значи, 30 + 13 = 43, т.е. оваа 2015 година Велигден ќе биде на 43-тиот ден од март, односно на 43 - 31 = 12 април.
Сега, да го пресметаме датумот на кој Велигден ќе се слави следната 2016 година..
Y = 2016
G = 1 + mod (2016, 19) = 1 + 2 = 3
E = mod (11 (3 – 3), 30) = 0
R = 21 + mod (54 – 0, 30) = 21 + 24 = 45
C = 1 + mod (45 + 2, 7) = 1 + mod (47, 7) = 1 + 5 = 6
N = 7 – mod (2016 + 4 + [2016 / 4], 7) = 7 – mod (2020 + 504, 7) = 7 – 4 = 3
S = 45 + 7 – mod (6 – 3, 7) = 52 – 3 = 49
Значи, според Јулијанскиот календар, следната 2016 година Велигден ќе биде на 49-тиот ден од Март, односно 49 – 31 = 18 април. Додека, според Грегоријанскиот календар, тоа ќе биде на 18 + 13 = 31-виот ден од април, што одговара на 1-ви мај.
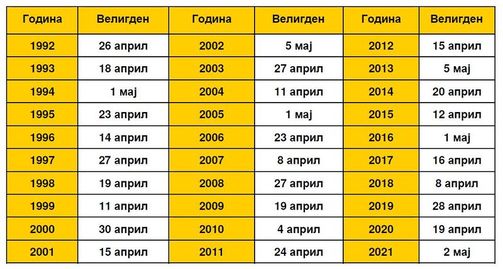
На Слика 3 е дадена табела со точните датуми на православниот Велигден, во текот на 30 години.
Слика3. Точните датуми на православниот Велигден
Извори:
[1] Ng Yoke Leng, The Sun in the Church, Department of Mathematics, National University of Singapore, 2002/2003
[2] Julian and Gregorian calenders, http://en.wikipedia.org/wiki/Conversion_between_Julian_and_Gregorian_calendars
Автор:
Ивона Ѓероска, студент на Институт за математика, Природно математички факултет, Скопје
Објавено на ПОИМ:
2 јуни 2015
Начин на цитирање на статијата:
И. Ѓероска, Мистеријата за датумот на Велигден, Портал ПОИМ на Институтот за математика, ПМФ, Скопје, 2 јуни 2015, http://poim-pmf.weebly.com/datumot-na-veligden.html
[1] Ng Yoke Leng, The Sun in the Church, Department of Mathematics, National University of Singapore, 2002/2003
[2] Julian and Gregorian calenders, http://en.wikipedia.org/wiki/Conversion_between_Julian_and_Gregorian_calendars
Автор:
Ивона Ѓероска, студент на Институт за математика, Природно математички факултет, Скопје
Објавено на ПОИМ:
2 јуни 2015
Начин на цитирање на статијата:
И. Ѓероска, Мистеријата за датумот на Велигден, Портал ПОИМ на Институтот за математика, ПМФ, Скопје, 2 јуни 2015, http://poim-pmf.weebly.com/datumot-na-veligden.html
Download (PDF)
Авторизираните статии објавени на Порталот подлежат на законска заштита. Се забранува користење на статиите без наведување на авторот или изворот.