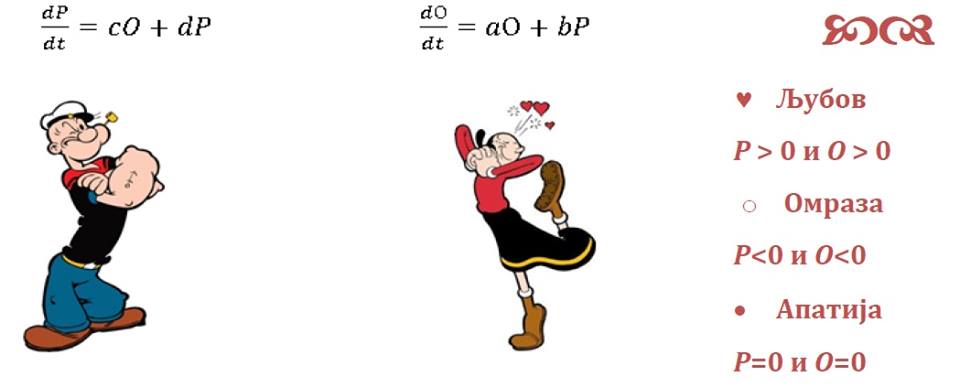1 / 2
|
(Не)Возможна ослободителна стратегија (PDF)
3 ноември 2021 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Математичките загатки отсекогаш привлекувале големо внимание кај секој од нас. Многу често на прв поглед тие изгледаат нерешливи, конфузни и многу комплицирани. Многу често имаме случаи во кои нашата цел не е решавање на загатката, туку разбирање на решението на загатката. Исто така, не се ретки случаите во кои врз база на даденото решение на една загатка, се обидуваме да најдеме нејзино поелегантно решение. Една таква загатка е и загатката позната под името 100 затвореници, која за прв пат била дадена во 2003 година од страна на данскиот компјутерски научник Питер Бро Милтерсен. Како што кажува и самото име на оваа загатка, станува збор за затвореници чија крајна цел е да добијат ослободителна пресуда, односно да ја победат управата на затворот во играта која се игра под одредени правила. Овој проблем е поставен во многу различни верзии, но секоја од нив ја има истата цел. Во продолжение ќе наведеме две познати верзии на овој проблем. Прво ќе ја наведеме првичната формулација на проблемот, а потоа верзијата во која најчесто се среќава овој проблем, т.е. формулацијата како загатка. Труд објавен во Математички омнибус 9 (2021). |
|
Фибоначиевите броеви, теоријата на Елиот и тргувањето со хартии од вредност (PDF)
25 октомври 2021 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Познато е дека Фибоначиевите броеви се појавуваат во математиката, посебно во геометријата при изучувањето на златниот пресек, како и кај разни „златни“ фигури, потоа кај Паскаловиот триаголник, но се појавуваат и на некои многу необични места: во природата, во архитектурата, во музичките форми и во економијата, посебно кај финансиските пазари. Финансиските пазари можат да се опишат како бикови или мечки. Биковите (анг. Bull markets) имаат растечка вредност на акциите и стабилна економија, додека кај мечките (анг. Bear markets) вредноста на акциите опаѓа и економијата е во рецесија. Интересно е тоа што ваквите пазари често сами себе се засилуваат поради тоа што исто така ги претставуваат мислите и очекувањата на инвеститорите. Да видиме како сето ова има врска со Фибоначиевите броеви. Елиот забележал дека пазарите мечки се состојат од 2 импулсивни бранови и 1 корективен бран, притоа формирајќи вкупно 3 бранови. Исто така, пазар бик се состои од 3 импулсивни, па 2 корективни бранови, со што се добиваат вкупно 5 бранови. Целосен пазарен циклус би бил комбинација од сите овие движења, односно би се состоел од 8 бранови... Труд објавен во Математички омнибус 9 (2021). |
|
Идентитетот на троен производ на Јакоби (PDF)
21 октомври 2021 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Во овој труд се презентира едноставен елементарен доказ на идентитетот на троен производ на Карл Густав Јакоби (1804-1851), кој претставува централен резултат во теоријата на елиптични функции. За соодветни вредности на 𝑞 и 𝑧, се добиваат класични идентитети познати од аналтичката теорија на броеви. Доказот е според презентацијата во книгата Квантна анализа (Quantum calculus) на Виктор Кац, која се заснова на теоријата на 𝑞 − редови. Ги даваме дефинициите на 𝑞 −дифернцијали и 𝑞 − биномни коефициенти и ги презентираме нивните основни својства. Од овие теореми на 𝑞 −анализа се изведуваат класичните биномни формули на Гаус и Хајне. Од нив, преку прост процес на определување гранична вредност, ќе се добијат познатите идентитети на Ојлер за 𝑞 − редови со бесконечно многу суманди. Труд објавен во Математички омнибус 9 (2021). |
|
Пандемиски игри и стратегии (PDF)
30 септември 2021 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Светот е исправен пред предизвиците на првата сериозна пандемија во вистински глобално поврзан свет. Најдени во една состојба на неизвесност, со многу непознати и неодговорени прашања, поединци, групи и глобални субјекти се обидуваат да ги најдат потребните одговори и да ги применат неопходните мерки. Не е тешко да разбереме дека преземените дејства подразбираат комплексна организација и координација на неколку нивоа. Државите, областите и регионите се налик на сврзани садови и ако некој од нив ја загуби контролата над ситуацијата, опасноста ќе се пренесе на други места. Така, богатите и развиени земји сфаќаат дека индивидуалните напори не се доволни и дека една навидум стабилна состојба може бргу да се влоши ако се појават сериозни епидемии во соседството, во неразвиени земји или области, или пак во случај на интензивна сообраќајна размена со ризични подрачја. Ова подразбира дека е потребна соработка (кооперативност) и не само координација за решавање на настанатите проблеми. Среде една, наизглед хаотична ситуација, и науката се обидува да помогне и да одговори на дел од прашањата. Но тоа не е воопшто лесно, земајќи предвид дека сериозните пандемии се ретки настани и едноставно нема доволно податоци од кои ќе се извлечат статистички значајни заклучоци. Труд објавен во Математички омнибус 9 (2021). |
|
Што е заедничко за мешање чај во шолја, боење темиња во триаголник и фер поделба на трошоци за станарина? (PDF)
29 септември 2021 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Колку добро може да измешаме чај во една шолја? Дали со таканаречено идеално мешање само во круг и без протресување на шолјата може да ја измешаме течноста толку добро, што по нејзиното сталожување сите молекули ќе бидат разместени во положба различна од почетната? Одговорот на ова прашање е негативен. Ако честичките чај во чашата ги сметаме за точки, тогаш (со занемарлива грешка) по секое мешање барем една молекула ќе се врати во почетната положба од којашто почнала да се движи. Овој заклучок му се припишува на холандскиот математичар Брауер (L. E. J. Brouwer). Тој ја формулирал и докажал познатата Tеорема на Брауер за неподвижна точка, од којашто директно следува заклучокот. Оваа теоремата заради едноставноста, и покрај тополошката природа, наоѓа примена во многу различни, па дури и неочекувани области, како што се економијата и теоријата на игри. Дел од заслугата за тоа имаат разните дополнувања на оваа теорема, како и тврдењата еквивалентни на неа. Интересен еквивалент на теоремата на Брауер од аспект на комбинаториката е Шпернеровата лема. Труд објавен во Математички омнибус 9 (2021). |
|
Декомпозиција на матрица на сингуларни вредности, анализа на нејзината временска и просторна сложеност и примена при компресија на слики (PDF)
6 септември 2021 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Идејата зад декомпозицијата на матрица на сингуларни вредности лежи во обопштувањето на спектралната декомпозиција или уште позната како факторизација со сопствени вредности којашто се изведува кај квадратните матрици. Декомпозицијата на матрица на сингуларни вредности има прилично долга историја, со тоа што првпат овој метод бил разгледуван од страна на математичарите во доцниот XIX век. Но, важните примени на оваа техника почекале сѐ додека пресметковната моќ на компјутерите не станала достапна во втората половина на XX век, кога биле развиени различни алгоритми за нејзина ефикасна имплементација. Во овој труд e претставена практичната примена на декомпозицијата на сингуларни вредности при компресија на дигитални слики, односно намалување на меморискиот капацитет којшто е потребен за нивно чување. Секако, треба да сме свесни дека SVD (Singular Value Decomposition) претставува компромис меѓу посакуваниот степен на компресија кој сакаме да го постигнеме и задржувањето на прифатлив квалитет на сликата, која нема да отстапува многу од оригиналот. Исто така, се соочивме со предизвици при преминот од теорија во пракса, при што ги искористивме знаењата од линеарна алгебра за да ја намалиме временската сложеност на овој алгоритам. На крајот, беше покажано дека со мала модификација на постапката, истиот метод може да се употреби за компресија и на црно-бели и на слики во боја. Труд објавен во Математички омнибус 9 (2021). |
|
Одлучувањето на младата популација во доменот на личните финансии: повеќекритериумски пристап (PDF)
30 јуни 2021 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Како едно од најбрзо растечките полиња на дисциплината операциони истражувања, повеќекритериумското одлучување се однесува на донесување одлука во услови на голем број критериуми кои можат да бидат меѓусебно конфликтни. Повеќекритериумското одлучување забележува огромна примена во последните неколку децении, во донесувањето одлуки во секојдневниот живот, но и во голем број други области: бизнис, образование, политика, медицина, животна средина, енергетика, спорт и др. Во процесот на одлучување во доменот на личните финансии постојат конфликтни критериуми при избирање на соодветната финансиска опција, особено кога се има предвид односот ризик – принос. Идеалната комбинација би била остварување на високи приноси, истовремено минимизирајќи ги ризиците, иако, во реалноста, средствата што имaат потенцијал да остварат високи приноси, обично носат и високи ризици. При одлучувањето во ситуации од секојдневниот живот, луѓето вообичаено донесуваат одлуки врз основа на интуиција. Од друга страна, за посложени проблеми, особено за оние што вклучуваат финансиска компонента, важно е проблемот да се структурира и да се вклучат повеќе критериуми во анализата. Труд објавен во Математички омнибус 9 (2021). |
|
Користење на матрична факторизација во системи за препорачување (PDF)
29 јуни 2021 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Под систем за препорачување се подразбира систем кој тежи да ја предвиди оцената или преферирањето на одреден објект од страна на специфичен корисник. Последните години ваков тип системи се неизбежен дел од платформите кои се трудат да го погодат вкусот на своите корисници и да им ги понудат оние производи или содржини кои ним најмногу би им се допаднале. Најпознат пример за ваков систем е платформата Нетфликс (Netflix) која врши селекција на филмови и серии кои би им се допаднале на нивните корисници. Ваквите системи добија најголема популарност кога оваа компанија го објави познатиот натпревар “The Netflix Prize”, во кој понудија еден милион долари на оној кој ќе го подобри постоечкиот систем за препораки за 10%. Во овој труд е анализирано решението кое победи на натпреварот, кое се базира на факторизација на матрици, односно запишување на матрицата од веќе дадени оцени, како производ од две други матрици. Труд објавен во Математички омнибус 9 (2021). |
|
Бриеровиот скор и предвидувачките турнири (PDF)
6 декември 2020 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Неизвесноста на идните настани и желбата да се знае што ќе се случи, кај секого буди интерес за предвидување. Интересот е помасовен, ако исходите од тие настани имаат глобално значење. „Колку случаи на заболени од COVID-19 ќе бидат регистрирани до 1 април 2021 година?“ е само едно од прашањата од глобален интерес во моментот на издавањето на овој труд. Слични актуелни прашања за настани во блиска иднина се поставуваат на предвидувачките турнири на кои индивидуалци или тимови се обидуваат да дадат веројатносна проценка за нивна реализација. Победник на предвидувачкиот турнир е тимот кој има најголема предвидувачка способност, која пак се мери со помош на Бриеровиот скор. Труд објавен во Математички омнибус 7 (2020). |
|
Демографските промени низ призмата на математичките модели (PDF)
2 септември 2020 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Уште во 17-тиот век, Џон Гронт (John Graunt, 1620 – 1674), ги поставил основите на демографијата како наука, истражувајќи ги неделните статистики на смртни случаи и крштевања во Лондон. Во 18-тиот век, оваа навидум општествена дисциплина, ја покажува својата интердисциплинарност, дел од научниот свет ја препознава како феномен со статистички правилности. Влечејќи информации од економијата, социологијата, статистиката, медицината, биологијата, антропологијата и историјата, демографијата станува основа за планирањето и општествен развој. Нашата идеја овде е да укажеме на важноста и примената на математичките модели без кои проекциите на населението и анализата на индексните стапки на смртност, новородени, фертилитет, миграција не би биле возможни. Труд објавен во Математички омнибус 7 (2020). |
|
Феноменот „Пропаст на коцкарот“ и случајното талкање (PDF)
20 август 2020 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Во последната деценија, коцкањето стана една од најпосакуваните „занимации“ ширум светот. Дел од луѓето кои се искусни во практикување на таа активност, вложуваат пари со надеж дека ќе добијат многу повеќе. Постојат и такви кои „пробуваат само еднаш“, а со самото тоа, свесно или несвесно, се доведуваат до работ да изгубат сè, т.е. до таканаречената пропаст на коцкарот. Во овој труд се презентирани генералните заклучоци добиени за коцкарот кој се обидел со постојано вложување (обложување) да освои максимални € N без да доживее коцкарска пропаст. Дали може да успее? Колкава е веројатноста да успее? И кое е очекуваното времетраење на една коцкарска игра до постигнување на посакуваната добивка или до коцкарската пропаст? Труд објавен во Математички омнибус 7 (2020). |
|
Формални граматики и нивна примена во дизајн на програмски јазици (PDF)
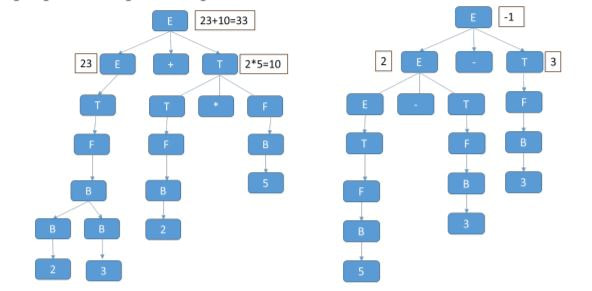
4 август 2020 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Формалните граматики несомнено претставуваат револуционен изум кој довел до развој на компјутерските науки, посебно развојот на програмските јазици како средство за комуникација помеѓу човекот и машината. Овој труд ја прикажува логичката страна, односно математичкиот концепт, за конструкција на една таква граматика. Разработката е направена преку илустрација на градењето на една од најосновните граматики, граматиката за формирање на правилни математички изрази, која е подмножество на секоја граматика за програмски јазик. Труд објавен во Математички омнибус 7 (2020). |
|
Игрите Еренфојт-Фрајсе: за логичките искази и строгите докази (PDF)
14 јули 2020 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Теоријата на игри е полна со длабоки загатки, кои се извор на чести несогласувања околу предложените решенија. Логичкиот пристап при решавање на ови проблеми се чини најсоодветен бидејќи се однесува директно на размислувањето, знаењето и спротиставеноста, како и поради неговата функција во утврдување на валидноста на аргументите. Игрите Еренфојт – Фрајсе се меѓу малкуте методи кои може да се применат кај конечните структури, а со тоа и во многубројни проблеми од компјутерската наука. Нивната примена е погодна и транспарентна кај релациони структури со унарни и бинарни релации, како што се графовите, линеарните и делумните подредувања, кои доминираат во многу области од компјутерската наука. Овие игри може да бидат интересни и за љубителите на креативни, но ригорозни математички докази. Труд објавен во Математички омнибус 7 (2020). |
|
Техники за генерирање случајни променливи во системи за масовно опслужување од типот M/M/n (PDF)
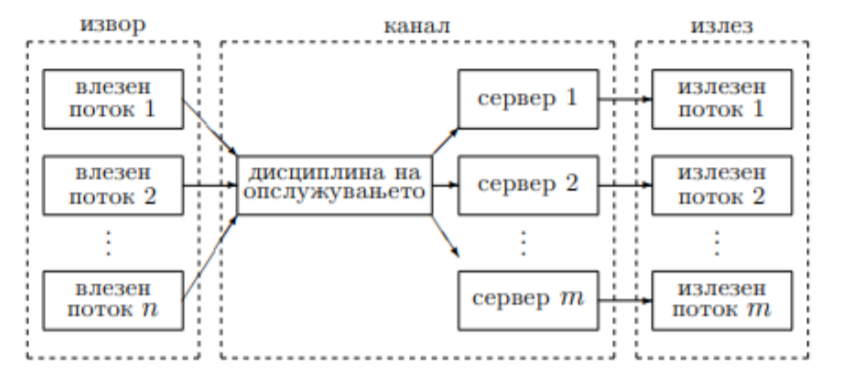
30 април 2020 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Теоријата на масовно опслужување е област во која се конструирани математички модели со чија помош може да се регулираат масовните појави од секојдневието. Имено, оваа област ни нуди можност да се справиме со редиците на чекање кои настануваат во банките, продавниците, бензинските пумпи, но и во централите до кои пристигнуваат некакви сигнали, итн. Едни од поедноставните модели на масовно опслужување се оние со Пoасонов влезен поток и експоненцијално време на опслужување. Со техниките за генерирање на случајните променливи од овие системи се обезбедува подобро разбирање на системите. Труд објавен во Математички омнибус 7 (2020). |
|
Визуализација на податоци (PDF)
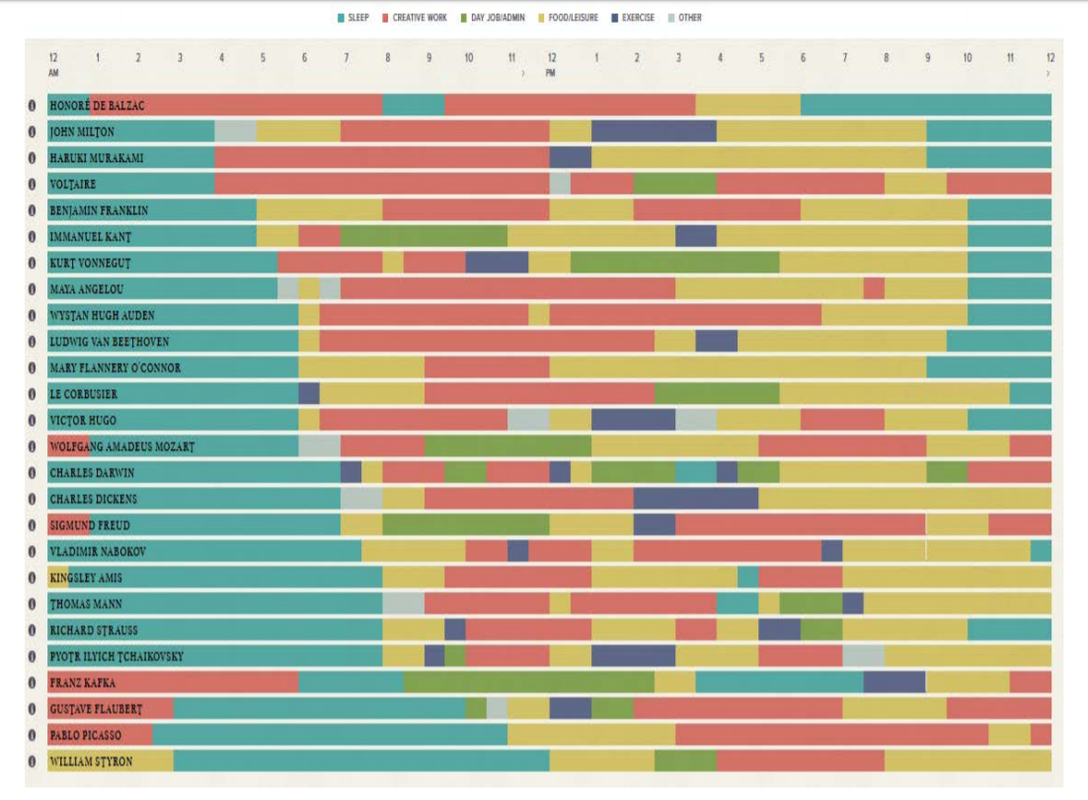
27 април 2020 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) „Визуализацијата ви дава одговори на прашања на кои не сте ни помислиле.“ – Бен Шнеидерман. Постојат многу различни дијаграми за визуализација на податоци, во основна и напредна верзија, нивни варијанти и комбинации, уредени во зависност од тоа што сакаме да потенцираме пред публиката. Визуализацијата е добра, кога е едукативна, дава реално значење на податоците, дава нова перспектива на веќе разгледуван проблем, ја предизвикува имагинацијата и љубопитноста на луѓето. Но, таа исто така може да биде и лоша, да ги искривува информациите и да го одвлекува вниманието од проблемот кој се разгледува. Труд објавен во Математички омнибус 7 (2020). |
|
Примена на диференцијални равенки во биологија (PDF)
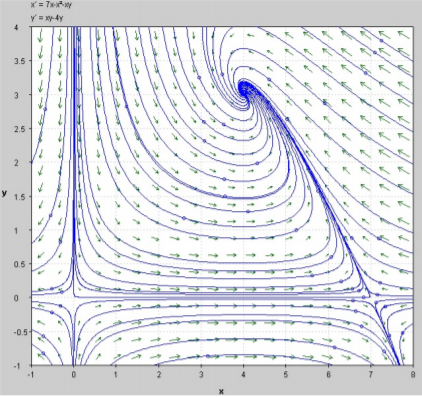
24 април 2020 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Разгледени се два различни биолошки модели кои се изразуваат преку нелинеарни системи од диференцијални равенки. Тие обично се поедноставни во идеални услови. Од друга страна, во природните процеси тешко може да се предвидат сите надворешни фактори, но сепак овие модели дават доволна индикација дека еколошките модели како и многу други природни појави се стремат кон стабилност. Труд објавен во Математички омнибус 7 (2020). |
|
Магични квадрати (PDF)
21 март 2020 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) За историјата на магичните квадрати, нивните општи својства, некои методи за конструирање на магични квадрати, геомагични квадрати, примена на магичните квадрати во наставата по математика и неколку сѐ уште нерешени проблеми за магичните квадрати. Труд објавен во Математички омнибус 7 (2020). |
|
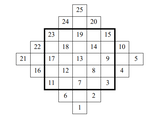
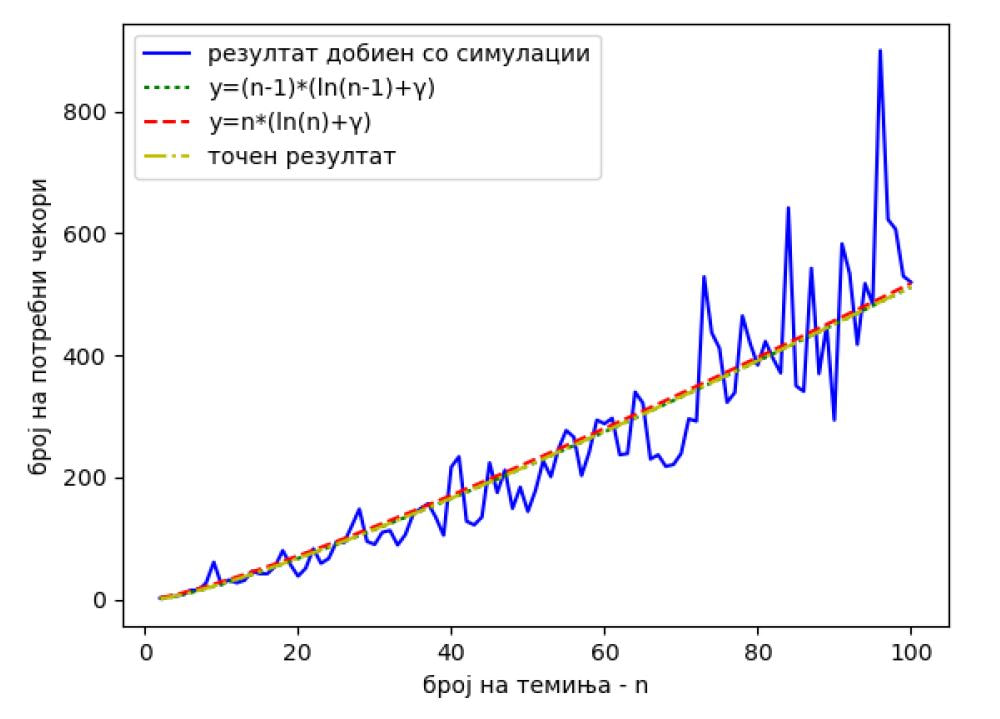
Теорија на графови и задачата на собирање купони (PDF)
11 јуни 2019 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Основната верзија на задачата на собирање купони гласи: Во секоја кутија со житарици има по еден купон кој носи одредена награда, така што постојат r различни видови награди. Еден човек купува по едно пакување од кутијата со житарици, сѐ додека не собере барем по еден награден купон од сите видови награди. Колку кутии со житарици треба да купи човекот? Решението на задачата на собирање купони може да го поистоветиме со очекуваното време за целосно покривање на комплетниот граф. Труд објавен во Математички омнибус 5 (2019). |
|
Шапли-Шубик индекс на моќност - од теорија до секојдневие (PDF)
7 јуни 2019 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Секој од нас се нашол во ситуација да направи избор во одреден момент, односно да се приклучи кон една или друга коалиција, кои застапуваат различни ставови, или поточно кажано се во конфликт. Притоа, важно е определувањето на оптималната стратегија, што може да се изведе со определување на интензитетот на важност на поединецот во групата, односно коалицијата. Труд објавен во Математички омнибус 5 (2019). |
|
Бинарни квадратни форми (PDF)
5 јуни 2019 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Наизглед едноставниот пробем на претставување на прост број како сума од два квадрати бил доволен поттик за формирање на теоријата на Лагранж за редукција на квадратни форми. Оваа теорија не само што целосно ги решава пробелмите на Ферма, туку нуди и алгоритамски пристап кон решавањето на слични проблеми од теоријата на броеви. Труд објавен во Математички омнибус 5 (2019). |
|
Обопштување на поимот функција: вовед во дистрибуции (PDF)
26 март 2019 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Кон средината на минатиот век, научниците согледале дека функциите и нивните својства не биле доволни за опишување на некои физички феномени. Потребата за обопштување на поимот функција довела до воведување на обопштените функции или дистрибуции. Развојот на теоријата на дистрибуции им овозможил на научниците да им дадат математичко значење на бројни пими кои до тогаш биле сфаќани интуитивно, како на пример Дираковата „функција“ и нејзините изводи. Труд објавен во Математички омнибус 5 (2019). |
|
Патување во времето (PDF)
26 март 2019 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Овој труд претставува еден обид да се одговори на некои прашања меѓу кои: 1. Дали светот во кој живееме е строго детерминиран во настаните, или, пак, ние можеме да влијаеме врз идните настани? 2. Дали постои машина – времеплов која би патувала низ времето (во минатото и во иднината), а ние визуелно или звучно би добиле некои информации во врска со патувањето? 3. Дали и луѓе би можеле да патуваат заедно со таа машина? 4. Која е научната основа на патувањето во времето? 5. Дали постојат паралелни светови? Труд објавен во Математички омнибус 5 (2019). |
|
На „темната страна“: од заблуда и манипулација до лага и измама (PDF)
17 март 2019 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Што сé може да се сретне на темната страна на математичката уметност? Броевите се моќно оружје, кои вешти раце можат лесно да ги претворат во средство за измама и манипулација, создадени се нови поими како математичарство и доказничарство. Од друга страна, пак, техниките на измама се издвоиле како своевиден биолошки механизам на преживување. Како се користат некои од овие техники, целите, пристапот и моделите кои притоа се применуваат, се разгледуваат низ теоретски и практични примери од економијата, политиката, теоријата на игри и хипер-игри. Труд објавен во Математички омнибус 5 (2019). |
|
Одлучување во услови на ризик и неизвесност (PDF)
15 февруари 2019 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Многу често кога треба да донесеме одлука треба да одбереме една од две или повеќе понудени можности без да бидеме сигурни за последиците од нашиот направен избор. Но, дали начинот на кој човекот одлучува може да се измоделира? Одговорот лежи во неколку теории за одлучување, почнувајќи од критериумот на очекувана вредност, теоријата на очекувана корисност, теоријата на перспектива и теоријата на кумулативна перспектива. Труд објавен во Математички омнибус 5 (2019). |
|
Примена на алгебарските хиперструктури во природните науки (PDF)
8 февруари 2019 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Кај хиперструктурите, наместо со обични алгебарски операции, се работи со таканаречени хипероперации, т.е. пресликувања од директниот производ на дадено множество H во непразни подмножества на тоа множество. Хиперструктурите се применуваат во математичките области како геометрија, комбинаторика, веројатност, критографија, но и во природните науки,во генетиката, физиката на елементарни честички и хемијата. Труд објавен во Математички омнибус 5 (2019). |
|
Интересни примени на теоремата на Стоун-Туки, Дирихлеовиот прицип на кутии и теоремата за стабилност (PDF)
27 јануари 2019 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Колку и да изгледа така, но математиката во суштина и не е толку апстрактна наука, математичките теореми колку и да звучат апстрактно и далечно, тие може да имаат сосема реални и понекогаш невообичаени интерпретации. Така математичките теореми може да ги сретнете кај сендвичот со шунка и кашкавал, кога ќе одите на забава или при организирање на екскурзија. Труд објавен во Математички омнибус 5 (2019). |
|
Окамовото сечило низ перспективата на Бејзовата статистика (PDF)
29 август 2018 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) „Ентитетите не треба да се размножуваат без потреба“ е позната изрека на франсискански монах, теолог и филозоф, Вилјам од Окам, чие модерно толкување е дека помеѓу повеќе хипотези треба да ѝ дадеме предност на онаа која е наједноставна. Може да се покаже дека овој принцип е последица на веќе познати тврдења од Бејзовата статистика. Труд објавен во Математички омнибус 3 (2018). |
|
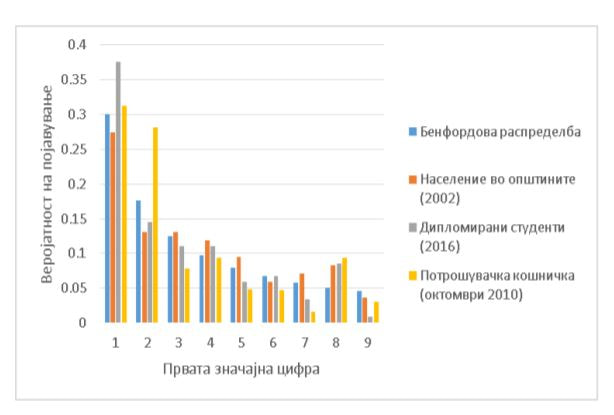
Законот на Бенфорд за првата значајна цифра (PDF)
29 август 2018 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Еден пример за универзалноста на математиката е токму законот на Бенфорд кој тврди дека првата значајна цифра кај броевите кои „потекнуваат од природата“ има логоритамска распределба. Токму овој „критерум за природност“ е искористен за откривање на финансиски измами, за дизајнирање на поефикасни компјутери, и воопшто за проверка на автентичноста и веродостојноста на влезните податоци и излезните резултати при работата со податоци во економијата, инженерството, медицината, психологијата итн. Труд објавен во Математички омнибус 3 (2018). |
|
Моделирање на Конвејовата ијра „Живот“ (PDF)
29 август 2018 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Играта „Живот“ е создадена од Џон Хортон Конвеј во доцните 60-ти години на 20-тиот век и таа се состои од поставување на пулови на бесконечна решетка и нивно придвижување според одредени правила. Таа е симулациона игра којашто може да создаде необични шеми со прекрасен изглед, а одредени нејзини почетни распореди може да се измоделираат во вид на задачи на математичко програмирање. Труд објавен во Математички омнибус 3 (2018). |
|
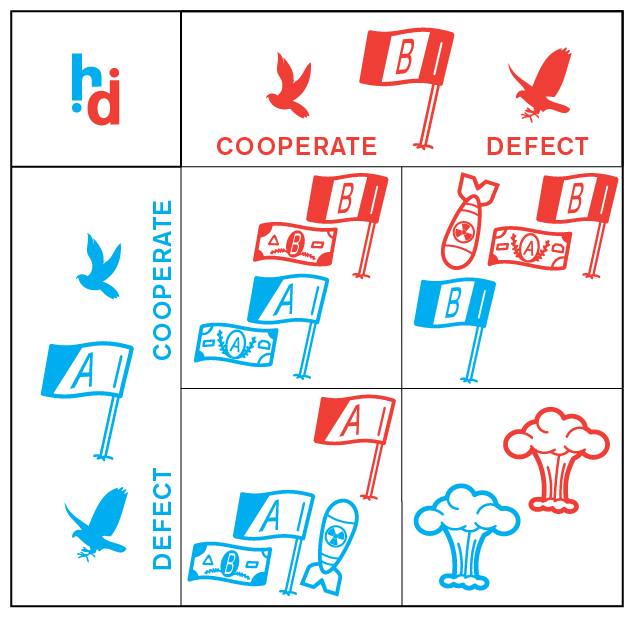
Затвореничка дилема: контекст, предизвици, варијации (PDF)
29 август 2018 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Затвореничката дилема е една од наедноставните 2х2 игри, која како никоја друга игра има добиено интезивно внимание и академска посветеност. Соодветниот одлучувачки парадокс кој таа го носи во себе, довел до многубројни надградби и варијации со широка примена во економијата, психологијата, спортот, заштита на околината, во меѓународната политика итн. Труд објавен во Математички омнибус 3 (2018). |
|
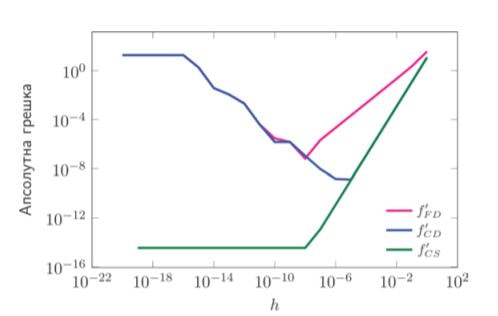
Нумеричка апроксимација на извод на функција од реална променлива со помош на имагинарен чекор (PDF)
29 август 2018 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Труд објавен во Математички омнибус 3 (2018). |
|
Зошто чиграта се движи по кружна траенторија? (PDF)
29 август 2018 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Труд објавен во Математички омнибус 3 (2018). |
|
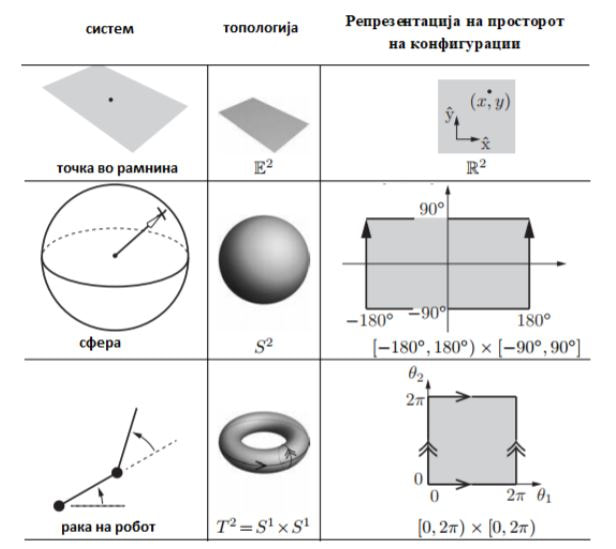
Простор на конфигурации на тополошки простор и негова примена во роботиката (PDF)
29 август 2018 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Труд објавен во Математички омнибус 3 (2018). |
|
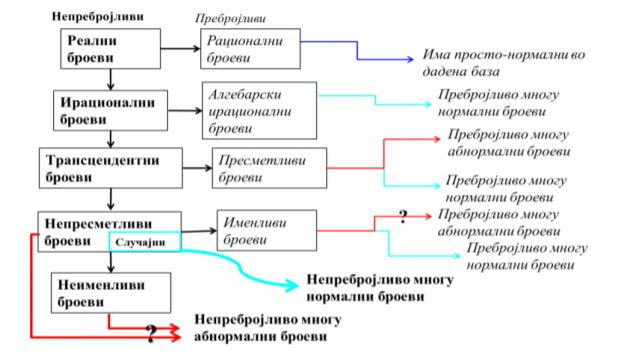
За нормалните и абнормалните реални броеви (PDF)
29 август 2018 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Труд објавен во Математички омнибус 3 (2018). |
|
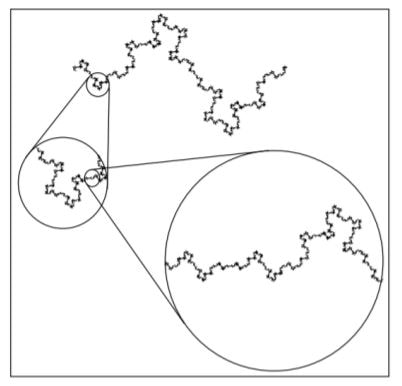
Фрактали: дефиниција, конструкција, својства и примена (PDF)
29 август 2018 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Труд објавен во Математички омнибус 3 (2018). |
|
Моќта и немоќта на очигледното во математиката (PDF)
29 август 2018 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Труд објавен во Математички омнибус 3 (2018). |
|
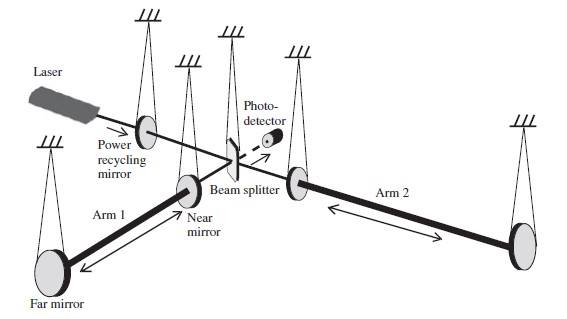
Гравитационите бранови како потврда на општата теорија на релативност (PDF)
23 септември 2017 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) За Ајншајновата теорија со која се предвидува постоење на бранувања на простор-времето кои се простираат како бранови и сокрешната емпириска потврда на таа теорија. Труд објавен во Математички омнибус 1 (2017). |
|
Љубовта како динамички систем (PDF)
23 септември 2017 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Анализа на нелинеарната динамика кога се појавува во една љубовна врска и соодветно предвидување на текот на љубовта. Труд објавен во Математички омнибус 1 (2017). |
|
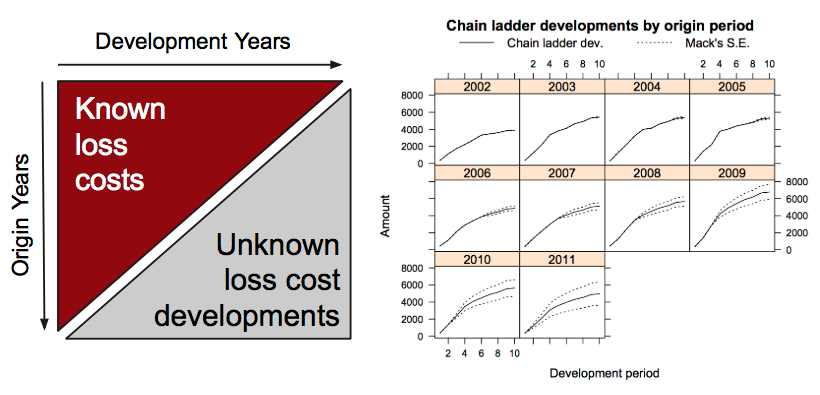
Предвидување на резервите за исплата на штетите при неживотно осигурување (PDF)
23 септември 2017 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Методот на триаголници за развој применет при предвидување на резервите на осигурителните компании за исплата на штетите. Труд објавен во Математички омнибус 1 (2017). |
|
Случајните процеси во неживотното осигурување (PDF)
23 септември 2017 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Моделирање на неизвесните процеси при решавање на проблемите кои вклучуваат ризик и несигурност на полето на осигурувањето и предвидување на вкупниот број на настанати штети. Труд објавен во Математички омнибус 1 (2017). |
|
Компресирање дигитални слики со примена на SVD разложување на матрици (PDF)
23 септември 2017 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Примена на резултати од линеарна алгебра за намалување на меморискиот капацитет на дигиталните слики и анализа на презентираната техниката. Труд објавен во Математички омнибус 1 (2017). |
|
Некои алгоритми за решавање на задачата на патувачкиот трговец (PDF)
23 септември 2017 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Едноставна формулација, широка примена, но тешка за решавање, задачата на патувачкиот трговец одсекогаш претставувала предизвик за решавање, иако за неа не постои начин да се предвиди колку долго би ја решавале, без да пробаме да ја решиме (NP-тешка задача). Труд објавен во Математички омнибус 1 (2017). |
|
Математиката на социјалните мрежи (PDF)
23 септември 2017 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Моделирање на социјалната поврзаност и некои посебни особености на социјалните мрежи. Труд објавен во Математички омнибус 1 (2017). |
|
Игри во економија, политика, војна: Колку сме навистина сериозни? (PDF)
23 септември 2017 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Поимите на натпревар, конфликт, соработка, наведување, убедување на другите да го прифатат нашето гледиште или прифаќање на туѓото, формирање на сојузи, на верувања, добивање и губење, се дел од вообичаената меѓучовечка интеракција, но и дел од математичка теорија која се занимава со игрите. Впрочем, се чини дека човекот сиот свој живот го поминува – играјќи. Труд објавен во Математички омнибус 1 (2017). |
|
Примена на топологијата во атмосферските науки за предвидување на атмосферски појави преку препознавање на облици (PDF)
23 септември 2017 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Како математиката може да помогне за предвидување на ураган, тајфун, тропска бура и слични атмосферски појави. Труд објавен во Математички омнибус 1 (2017). |
|
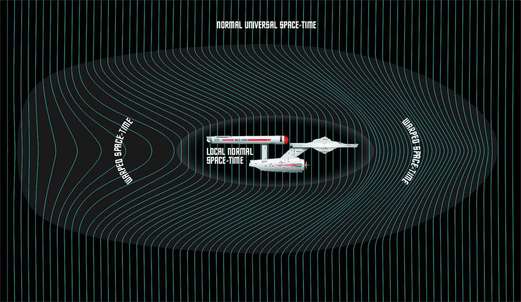
Математиката на иднината - патување со натсветлински брзини (PDF)
23 септември 2017 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) За принципот на работа на ворп-погонот на Алкубиере којшто овозможува движење со брзини поголеми од брзината на светлината. Труд објавен во Математички омнибус 1 (2017). |
|
Математички модел на францускиот парадокс (PDF)
23 септември 2017 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Зошто французите имаат релативно мала веројатност да заболат од срцеви коронарно-артериски заболувања, иако исхраната им се состои од храна богата со заситени масти? Труд објавен во Математички омнибус 1 (2017). |
|
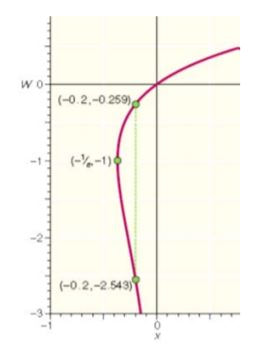
Ламбертова функција - график, пресметки и примена (PDF)
23 септември 2017 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) За математичката функција која дава затворен облик на решенијата на повторувачките појави во природните, општествените и инженерските науки. Труд објавен во Математички омнибус 1 (2017). |
|
Големата теорема на Ферма (PDF)
23 септември 2017 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Осврт на една од најфамозните теореми за човештвото, животот и залагањата на Ферма, обидите за докажување на теоремата и големото откритие на Ендру Вајлс. Труд објавен во Математички омнибус 1 (2017). |
|
Шеми за распоредување на простите броеви (PDF)
23 септември 2017 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Простите броеви ги фасцинираат математичарите од најстари времиња. Тие, навидум се појавуваат случајно, но и не толку случајно. Труд објавен во Математички омнибус 1 (2017). |