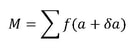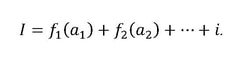СТАТИИ ЗА НАСТАВАТА ПО МАТЕМАТИКАСе залагаме за зголемување на свеста за местото и улогата на математиката во науките, технологијата, наставата, природата и културата.
|
МАТЕМАТИКАТА И ПРАВОТО
Потрагата по вистината и нејзиното докажување е заеднички предизвик за математиката и правото Во математиката, основните поими и аксиоми се темел на изведените тврдења и секоја друга вистина е во согласност со другите, добиена по пат на логичко заклучување. Дали уредниот и сеопфтен доказ кој математичарите сакаат да го прочитаат за да бидат убедени во кажувањето на теоремите е завршниот говор на правните случаи кон којшто целат адвокатите?
Ќе разгледаме неколку примери во кои математиката, во елементарна или во посложена форма, му помага на правото.
1. Проценти
Ќе разгледаме неколку примери во кои математиката, во елементарна или во посложена форма, му помага на правото.
1. Проценти
|
При основањето фирма или трговско друштво, уделот што го има секој од содружниците е соодветниот процент од сопственоста. Операциите со проценти се користат во процедурата за пренос на удел или продажба на дел од фирмата. Да разгледаме еден пример.
Двајца партнери основале фирма со основна главнина од 10000 евра. Ако првиот вложил 7000 евра, а вториот 3000 евра, нивниот удел во фирмата е 70% и 30%, соодветно. |
По неколку години, фирмата остварила напредок и цела нејзината вредност изнесува 1 милион евра. Сега, паричната вредност на уделот од првиот партнер изнесува 700 000 евра. Да претпоставиме дека тој сака да продаде 10% од својот дел од фирмата на трето лице. Тогаш, книговодствената вредност на тој дел изнесува 10% од 700 000 евра, т.е. 70 000 евра. Да забележиме дека, третиот сопственик сега поседува 10% од 70% од фирмата, т.е. 1/10 x 70/100 = 7/100 од фирмата, т.е. 7% од фирмата.
Слично е регулиран уделот кој го имаат инвеститорите во стартап компаниите. Ова значи дека вредноста на инвестираната сума се менува пропорционално со растот на компанијата, па затоа поисплатливо е инвестирањето во добри бизнис идеи, отколку штедењето во банка.
|
2. Анализа на случај
Методите на логичко заклучување – анализа, синтеза, дедукција, аналогија, важат и во правото. Секој правен случај којшто личи на други случаи, а истовремено е и уникатен, адвокатите го анализираат онака како што математичарите решаваат задача. Дадената ситуација се разделува на составни компоненти коишто се истражуваат, а потоа спојуваат, за да се комплетира целокупната слика. Тоа потсетува на изведување математички доказ. |
За да се пронајде соодветниот член во законот и правилно да се протолкува во потребниот контекст, природно е користењето на логичките операции и на операциите со множества (и=пресек, или=унија, или-или=симетрична разлика), а тие можат да се применат и на интервали, особено кај членови од законот коишто се поврзани со услови и временски рокови.
3. Математички модели
Математичките формули служат за јасни и концизни проверки и резултати кои може да помогнат и при правни одлуки. Еден таков пример е во определувањето дали некој пронајдок е патент или не.
Генералните услови коишто кандидатот за патент треба да ги исполнува се:
I. Да биде патентибилен – содржина која може да биде заштитена со патент,
II. Да биде целосно или барем делумно нова содржина,
III. Да не е очигледна последица на нешто познато,
IV. Да биде нешто корисно (да има индустриска примена).
Математичките формули служат за јасни и концизни проверки и резултати кои може да помогнат и при правни одлуки. Еден таков пример е во определувањето дали некој пронајдок е патент или не.
Генералните услови коишто кандидатот за патент треба да ги исполнува се:
I. Да биде патентибилен – содржина која може да биде заштитена со патент,
II. Да биде целосно или барем делумно нова содржина,
III. Да не е очигледна последица на нешто познато,
IV. Да биде нешто корисно (да има индустриска примена).
Во 1013 година, Harold E. Potts предложил математички начин за проценување на иновацијата во продуктите. Имено, тој секоја идеја чијшто „технички ефект“ треба да боде проценет, ја запишувал како функција I = f(x). Под поимот функција подразбираме законитост според којашто еден процес зависи од еден или од повеќе фактори, коишто ги викаме аргументи или независни променливи. Со a,b,... се означуваат познатите параметри, а со x,y,z,... се означуваат новите променливи. Така, на пример, идеите од облик f(a) или f(b) не се иновации. Исто така не се иновации и линеарните комбинации од вакви функции. Линеарна комбинација од функции е функција која е добиена како збир од вакви „познати“ функции, производ од познат параметар (б) и ваква функција или, пак, комбинација од овие две операции. Она што би било иновација е од облик I = M + i, каде што
а i е ефектот на иновативност. Со други зборови, иновацијата може да ги користи претходно познатите пронајдоци, материјали и методи, но да воведе нешто ново што ќе биде револуционерно во таа област. Во овој модел, иновациите се поделени во категории на следниов начин:
i) Комбинација – иновација добиена со комбинирање на постоечки пронајдоци и нешто ново:
ii) Постигнување екстремна вредност на функција за конкретна вредност на некоја променлива – ова е иновација во којашто се открил минимален или максимален ефект од некој претходно познат процес. На пример, процесот да го означиме со М = f (a, b, c), каде што а, b, c се променливите од кои зависи тој процес. Ако сме нашле конкретна вредност c_1 за променливата c за којашто се остварува екстремен исход од тој процес, тогаш тоа значи дека изводот на функцијата f по променливата c, пресметан во c_1 е еднаков на нула или не постои.
Еден ваков пример е светилката на Едисон. Едисон не ја измислил електричната светилка, туку ја подобрил функционалноста на постоечката со користење на карбонско влакно. Вака, светилката била многу поиздржлива и затоа ваквите светилки биле многу комерцијално распространети.
iii) Иновација е нов начин на користење на некој материјал или ресурс. Ако а е тој ресурс кој претходно се користел на f (a) начин, а сега е понудена употреба на g (a) начин, тогаш g е нова функција.
Пример за ваков патент е случајот на Penn v. Bibby, каде што е предложена употреба на дрво како материјал за лежиште на пропелерите од брод. Дотогаш дрвото се користело за „водени тркала“, но овој начин на употреба бил нов.
iv) Иновација е и користење на различен материјал или ресурс во познат процес. За разлика од iii), овде се менува аргументот, а не функцијата, т.е. иновацијата е од облик f (x).
v) Состав од функции – ова е функција која е добиена како функција од друга функција. Ако f (a) е она што е познато, а сега е понудено негово користење во нов процес F, тогаш обликот на иновацијата е F(f (a)).
Користена литература:
[1] https://archive.org/details/paper-doi-10_1038_091187c0/page/n1/mode/2up
[2] https://www.aleksov.mk/mk/konvertibilen-zaem/
[3] Report of patent, design, and trade mark cases decided by courts of law in the United Kingdom: Vol. III., No. 12. Friday, July 2, 1886.
Автор: Гордана Николовска, наставник по математика во СУГС„Георги Димитров“ и уредувач на информативни содржини за Aдвокатска канцеларија Алексов
Објавено на ПОИМ: 21.8.2020 година
Начин на цитирање на статијата:
Г. Николовска, Математиката и правото, Портал ПОИМ на Институтот за математика, ПМФ, Скопје, 22 август 2020,
[1] https://archive.org/details/paper-doi-10_1038_091187c0/page/n1/mode/2up
[2] https://www.aleksov.mk/mk/konvertibilen-zaem/
[3] Report of patent, design, and trade mark cases decided by courts of law in the United Kingdom: Vol. III., No. 12. Friday, July 2, 1886.
Автор: Гордана Николовска, наставник по математика во СУГС„Георги Димитров“ и уредувач на информативни содржини за Aдвокатска канцеларија Алексов
Објавено на ПОИМ: 21.8.2020 година
Начин на цитирање на статијата:
Г. Николовска, Математиката и правото, Портал ПОИМ на Институтот за математика, ПМФ, Скопје, 22 август 2020,
Download (PDF)
Авторизираните статии објавени на Порталот подлежат на законска заштита. Се забранува користење на статиите без наведување на авторот или изворот.