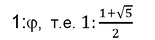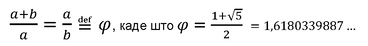СТАТИИ ОД МЕСЕЦОТ НА НАУКАТА​

Се залагаме за зголемување на свеста за местото и улогата на математиката во науките, технологијата, наставата, природата и културата.

Златни фигури

Златни фигури се многуаголници кај кои должините на страните или дијагоналите се во златен сооднос
или околу 1:1,618. Во математиката, две величини се во златен сооднос ако соодносот помеѓу двете величини е еднаков на збирот на тие две вредности, наспроти величината со поголема вредност. Алгебарски, за а и b и a>b>0 тоа може да се запише вака:  : 
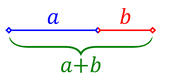
Злaтниот сооднос се нарекува и златен пресек. Златниот пресек (φ) е прикажан како отсечка поделена на два дела a и b, така што, односот на должината на отсечката a+b и поголемата страна a е еднаков на односот на поголемата страна a и помалата страна b, т.е.
ЗЛАТЕН ПРАВОАГОЛНИК
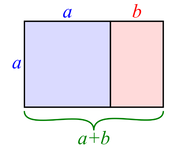
​Златниот правоаголник е правоаголник со должина на страните во златен сооднос 1:φ. Кога златниот правоаголник со подолга страна a и пократка страна b е поставен до квадрат со страна со должина a, формира сличен златен правоаголник со подолга страна a+b и помала страна a. Тоа е илустрирано со соодносот 
                                                                        φ = (a + b) : a =  a : b


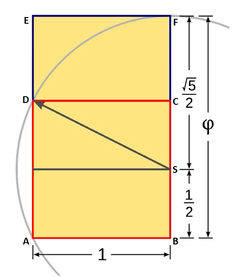
​Златниот правоаголник може да се конструира само со шестар и линијар следејќи ја оваа постапка:  
  • Нацртајте квадрат со должина на страна 1.
  • Повлечете отсечка од средината S на една страна на квадратот, на пример BC, до спротивниот агол, соодветно во примерот ADC.
  • Таа отсечка SD е радиус на лак со центар во S кој ја определува ширината на правоаголникот (должината е 1). Пресекот на тој лак со продолжението на страната BC го дава темето F на златниот правоаголник. 
  • Доврешете го златниот правоаголник, повлекувајќи ги отсечките EF и АЕ, паралелно со страните AB и BC, соодветно. 
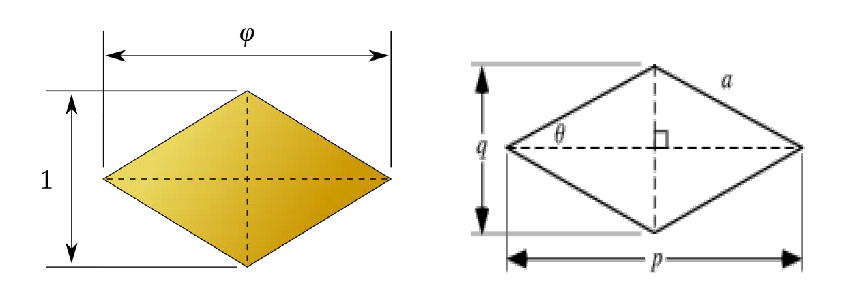
ЗЛАТЕН РОМБ
Златен ромб е фигура кај која дијагоналите се во сооднос p : q = φ. Плоштината на ромбот е ​φ / 2.
ЗЛАТЕН ТРИАГОЛНИК
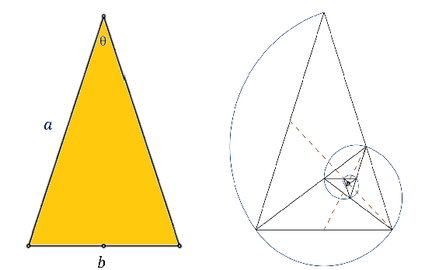
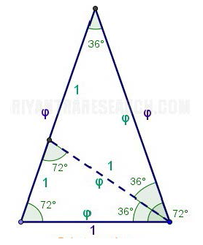
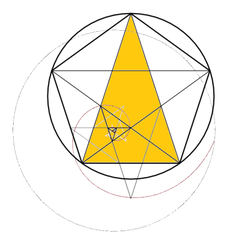
Златен триаголник е рамнокрак триаголник во кој краците се во златен сооднос со основата т.е. a : b = φ. На црежот долу десно се дадени златни триаголници впишани во златна спирала. 
  • Златниот триаголник е единствен триаголник кај кој односот на внатрешните агли е 2:2:1, т.е аглите на основата се 72 степени, а аголот на врвот е 36 степени. 
  • ​Ако кај златниот триаголник повлечеме симетрали на аглите на основата, пресечната точка на симетралите, пресечната точка на една симетрала на аголот со кракот и едно теме кај основата на триаголникот формираат повторно златен триаголник.
  • Оваа постапка можеме да ја продолжиме до бесконечност, при што се формираат бесконечен број златни триаголници чиишто темиња формираат низа точки на златна спирала.
НАОЃАЊЕ НА ЗЛАТНИТЕ ФИГУРИ
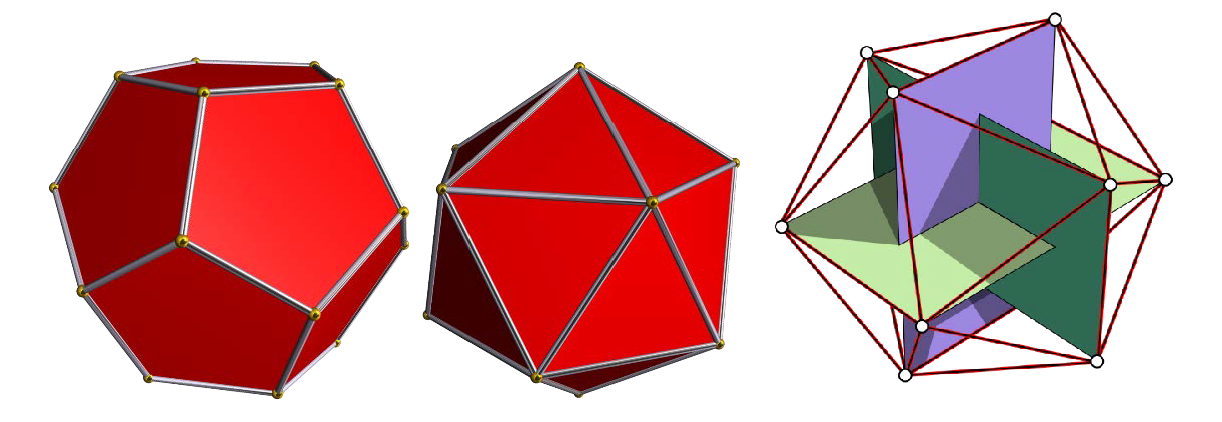
​Златните триаголници и правоаголници се наоѓаат во мрежите на додекаедар и икосаедар.
​Златните триаголници се наоѓаат во правилнот петаголник и кај пентаграмот.
ЗЛАТЕН ПРЕСЕК ВО ПРИРОДАТА
Златниот пресек се јавува во природата: кај распоредот на цветните ливчиња (тоа е идеален распоред при Дарвиновиот процес - секое ливче е распоредено на 0.618034 по завртување - од полно завртување од 360 степени); златниот правоаголник се појавува и кај школката наутилус, се јавува кај човечката рака (конкретно кај прстите), се јавува и кај телата на инсектите, при распоредот на гранките и листовите на дрвјата, кај ДНК структурата, но и при формирањето урагани и галаксии ([5]). 
Користена литература:
[1] Златен правоаголник - Википедија, https://mk.wikipedia.org/wiki/Златен_правоаголник
[2] Golden triangle (mathematics - Wikiwand, https://www.wikiwand.com/en/Golden_triangle_(mathematics)
[3] Златен пресек - Википедија, https://mk.wikipedia.org/wiki/Златен_пресек
[4] Golden fhombus - Wikipedia, https://en.wikipedia.org/wiki/Golden_rhombus
[5] 15 Uncanny Examples of the Golden Ratio in Nature, https://io9.gizmodo.com/15-uncanny-examples-of-the-golden-ratio-in-nature-5985588

​Автор: 
Ана Гражданлиевска VIII одд., ООУ „Гоце Делчев“ Босилово
Проект презентиран на Ноември – Месец на науката 2019 во категоријата 7-9 одд.

Професор: 
Цвета Спасковска

Објавено на ПОИМ:
30 март 2020 година

Начин на цитирање на статијата:
A. Гражданлиевска, Златни фигури, Портал ПОИМ на Институтот за математика, ПМФ, Скопје, 30 март 2020 год., ​​http://poim-pmf.weebly.com/zlatni-figuri.html
Авторизираните статии објавени на Порталот подлежат на законска заштита. Се забранува користење на статиите без наведување на авторот или изворот.
Copyright © 2015 POIM