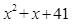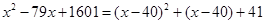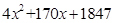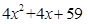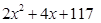Spirala od prosti broevi

НАУЧНО - ПОПУЛАРНИ СТАТИИ

Се залагаме за зголемување на свеста за местото и улогата на математиката во науките, технологијата, наставата, природата и културата.

СПИРАЛА ОД ПРОСТИ БРОЕВИ

(Темата е презентирана и на Првиот семинар „Математика и примени“, 14 декември 2016)
(апстракт), (презентација), (ПОИМ статија), (труд)

Секој природен број поголем од 1, што е делив самo со 1 и сам со себе се вика прост број. Запишани во низа, тоа се броевите: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31,... Наједноставен начин за наоѓање на простите броеви е Ератостеновото сито (Ератостен, 276-194 година пред н.е.). Тоа е едноставен алгоритам којшто се состои во следното. Се запишува низата од природни броеви поголеми или еднакви на 2:

2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, ...

Прво, се пречкртуваат броевите во низата што се поголеми од 2 и се деливи со 2 (тоа се: 4, 6, 8, 12, ...), т.е. секој втор број. Потоа, од преостанатите броеви, го наоѓаме најмалиот број што е поголем од 2, т.е. бројот 3 и ги пречкртуваме сите броеви поголеми од 3 што се деливи со 3 (тоа се: 6, 9, 12, 15, 18,...). Ако во низата се испишани n природни броеви, постапката ја продолжуваме натаму сé до најголемиот природен број што е помал или еднаков на n/2.

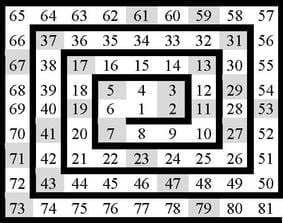
До денес, не постои формула за одредување на простите броеви. Ниту една комбинација на алгебарски операции не го дава, на пример, стотиот прост број. Сепак, постојат шеми коишто даваат барем некакво чувство за ред меѓу простите броеви. Еден посебно интересен пристап за разгледување на простите броеви е Уламовата спирала. Називот доаѓа од презимето на полско-американскиот математичар Станислав Улам (1909-1984).

Спиралата се конструира на следниов начин: се почува од 1. Потоа, до него од десната страна се пишува 2, над 2 се пишува 3, до 3 одлево се пишува 4 (така 4 доаѓа над 1), па лево од 4 се пишува 5, итн., како на цртежот прикажан подолу, спротивно од стрелките на часовникот се пишуваат сите останати природни броеви. Со сиво се обележани полињата на простите броеви.

Во врска со конструкцијата на оваа спирала постои една анегдота. Во 1963 година, присуствувајќи на нечие долго и здодевно излагање на научна конференција, Улам почнал да ги пишува природните броеви во спирала, онака како што ги испишавме на цртежот, и почнал да ги заокружува простите броеви. Изненадено забележал дека простите броеви се редат по прави линии или, како што рекол, „имаат тенденција на неслучајно појавување“. По враќањето во лабораторијата во Лос Аламос, сакал да ја види оваа шема за повеќе броеви. Искористувајќи магнетна лента што ги забележувала првите 90 милиони прости броеви, тој и неговите соработници Мајрон Л. Стајн (Myron L. Stein) и Марк Б. Велс (Mark B. Wells), го програмирале лабораторискиот компјутер Maniac II за да ги прикаже простите броеви во спирала на 65000 последователни природни броеви, како светлечки точки во туба на осцилоскоп поврзана со компјутерот. Направиле фотографија и добиле изненадувачки образец (шара), која ги прикажувала простите броеви не само во дијагонални, туку и во хоризонтални и вертикални прави (слика долу лево). Овие прави не се појавуваат кога станува збор за спирала од прости броеви на случајно одбрани природни броеви (слика долу десно).

Овие прави, односно полуправи, кои почнуваат од некој број и се или вертикални или хоризонтални или имаат коефициент на правец 1 или -1, навестуваат формули за простите броеви. Денес е познато дека тие најчесто можат да се опишат со помош на квадратни триноми во кои првиот член е 4x^2. До тој заклучок се стигнува преку табелата од разлики што се формира од почетната низа. На пример, една дијагонална низа ги вклучува простите броеви 5, 19, 41, 71 и 109. Ако на x му доделиме вредности од 0 до 4, ќе ги добиеме броевите 5, 19, 41, 71 и 109 кои се прости, но за x=5 се добива бројот 155, кој очигледно не е прост. Табелата од разлики на оваа низа е:

Како што можеме да видиме од табелата, вторите ралики се исти, па ова ни кажува дека почетната низа може да се опише со помош на полином од втор степен. Полуправата на која ѝ припаѓаат овие броеви може да се опише со алгебарскиот израз (познат како Ојлеров полином):

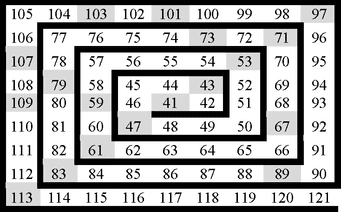
Една спирала може да започне и од некој друг број што не е 1. Да земеме, на пример, шемата да започнува со бројот 41 (види го следниот цртеж). По дијагоналата на оваа спирала се добива низа од 40 прости броеви без прекин. Тие можат да се добијат со помош на формулата што е дадена погоре, што е всушност, најпознатата формула за генерирање прости броеви. Интересно е дека од првите 2398 броеви генерирани со оваа формула точно половината се прости броеви. Проверувајќи ги броевите помали од 10 милиони, Улам и неговите соработници утврдиле дека односoт меѓу простите и сложените броеви е 0,475.

Може да се добијат 80 последователни прости броеви со трансформирање на Ојлеровата формула до формулата

Постојат и други формули што се богати со прости броеви. На пример, за броевите од облик

односот меѓу простите и сложените броеви е 0,466, додека за оние од облик

односот е 0,437. Постојат и квадратни триноми што ретко даваат прости броеви. На пример, изразот

води до прост број во само 5% од случаите.

Улам предложил неколку проблеми за натамошно истражување. На пример:

Постојат ли прави (полуправи) со бесконечно многу прости броеви?
Дали распределбата на прости броеви во секој квадрант е иста?

Уламовата спирала не е многу испитувана. На пример, сè уште не е јасна причината за дијагоналното, вертикалното и хоризонталното разместување на простите броеви. Сепак, таа е значајна зашто покажува постоење на јасен образец кој постои меѓу простите броеви. Тој, пак, може да овозможи откривање на нови полиноми што ќе генерираат повеќе прости броеви од претходно најдените. Тие можеби ќе водат до подобро разбирање на многу интерсни хипотези, како што е, на пример, Голдбаховата хипотеза (за неа можеш повеќе да прочиташ во претходна статија објавена на ПОИМ) или хипотези во врска со простите броеви.

Една занимливост во врска со оваа спирала. Познатиот писател на научна фантастика Артур Кларк, во својот роман „Градот и ѕвездите“ (во оригинал: The City and the Stars) објавен во 1956 година, ја опишал оваа спирала. Настаните во делото се случуваат 1 000 000 000 години во иднината, во градот Дијаспар. Земјата е толку стара, што океаните ги нема, а човештвото скоро исчезнато.

Извадок од делото: „Џесерак седеше неподвижно во вртлогот од броеви. Првите 1000 прости броеви... Тој не беше математичар, иако понекогаш сакаше да верува дека е. Сè што можеше да стори е да бара врски и правила меѓу бесконечната низа од прости броеви што поталентирани луѓе би можеле да ги преточат во општи закони. Можеше да најде како се однесуваат некои броеви, но не можеше да објасни зошто. Му беше задоволство да го пробива својот пат низ аритметичката џунгла и некогаш откриваше чуда што повешти истржувачи ги пропуштиле. Тој ја состави матрицата од сите можни природни броеви, а компјутерот започна да ги ниже простите броеви по површината, како перли што можат да се распоредат на пресеците на една решетка.“ (превод на авторот од англиски).

Задачи за вежбање.
1. Направи спирала која почнува од 17.
а) Најди колку прости броеви последователно можат да се добијат со помош на изразот 4x^2+2x+17.
б) Најди колку прости броеви последователно можат да се добијат со помош на изразот x^2+x+17.
2. Обиди се да најдеш алгебарски израз кој ги опишува простите броеви во низата 7, 23, 47, 79, ...
(Одговор: 4x^2+4x-1).

Извори:
[1] A visual analysis of prime number distribution
[2] Prime spiral, WolframMathWorld
[3] http://scienceblogs.com/goodmath/2010/06/22/the-surprises-never-eend-the-u/

Автор:
Весна Целакоска-Јорданова, Институт за математика, Природно-математички факултет, Скопје

Објавено на ПОИМ:
5 јануари 2017

Начин на цитирање на статијата:
В. Целакоска-Јорданова, Спирала од прости броеви, Портал ПОИМ на Институтот за математика, ПМФ, Скопје, 5 јануари 2017, http://poim-pmf.weebly.com/spirala-od-prosti-broevi.html

Dowload (PDF)

Авторизираните статии објавени на Порталот подлежат на законска заштита. Се забранува користење на статиите без наведување на авторот или изворот.