|
СТАТИИ ОД МЕСЕЦОТ НА НАУКАТАСе залагаме за зголемување на свеста за местото и улогата на математиката во науките, технологијата, наставата, природата и културата.
|
|
ПРАВИЛНИ ПОЛИЕДРИ - ЗОШТО ПЕТ?
Полиедар (или рабесто тело) е фигура ограничена со површини коишто се составени само од многуаголници. Многуаголниците што ја образуваат површината (т.е. „границата“) на полиедарот се викаат ѕидови, нивните страни се викаат рабови, а нивните темиња се темиња на полиедарот. Во секое теме на еден полиедар се сретнуваат барем три негови рабови, а секој раб е страна на два и само на два негови ѕидови. Конвексен полиедар е полиедар којшто се наоѓа на иста страна од рамнината на кој било негов ѕид. За еден конвексен полиедар велиме дека е правилен ако сите негови ѕидови се правилни многуаголници. Постојат само пет правилни полиедри уште познати како Платонови тела. Кои се правилните полиедри и зошто ги има само пет?
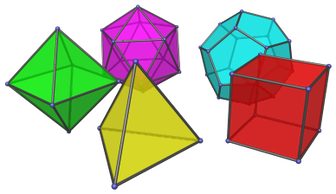
Петте правилни полиедри се:
Петте правилни полиедри се:
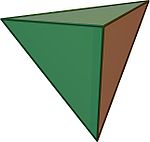
- Правилен тетраедар – чии ѕидови се четири рамнострани триаголници.
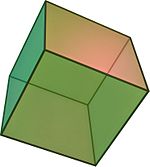
- Правилен хексаедар (коцка) – чии ѕидови се шест квадрати.
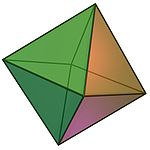
- Правилен октаедар – чии ѕидови се осум рамнострани триаголници.
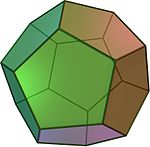
- Правилен додекаедар – чии ѕидови се дванаесет правилни петаголници
- Правилен икосаедар – чии ѕидови се дваесет рамнострани триаголници.
|
Правилен тетраедар
Правилниот тетраедар е полиедар составен од четири рамнострани триаголници, од кои три се среќаваат во секое теме. Тетраедарот е вид на пирамида.Тетраедарот има: 4 ѕидови, 4 темиња и 6 рабови. |
|
|
Правилен хексаедар (Коцка)
Хексаедар е секое тело составено од шест ѕидови. Правилен хексаедар (коцка) е полиедар составен од шест квадрати, од кои три се среќаваат во секое теме. Правилниот хексаедар има: 6 ѕидови, 8 темиња и 12 рабови. |
|
|
Правилен октаедар
Правилниот октаедар е полиедар составен од осум рамнострани триаголници, од кои четири се среќаваат во секое теме. Октаедарот има 8 ѕидови, 6 темиња и 12 рабови. |
|
|
Правилен додекаедар
Додекаедар е тело составено од дванаесет ѕидови. Правилниот додекаедар е составен од дванаесет правилни петаголници, од кои три се среќаваат во секое теме. Додекаедарот има 12 ѕидови, 20 темиња и 30 рабови. |
|
|
Правилен икосаедар
Правилниот икосаедар е составен од дваесет рамнострани триаголници, од кои пет се среќаваат во секое теме. Икосаедарот е правилен полиедар со најголем број ѕидови. Икосаедарот има: 12 ѕидови, 12 темиња и 30 рабови |
|
Доказ дека постојат само пет правилни полиедри
Постојат повеќе докази за докажување дека постојат само пет правилни полиедри. Еден од нив е со помош на големината на аглите кои се среќаваат во секое теме. Наједноставната причина зошто има само пет правилни полиедри е следнава:
Во секое теме мора да се среќаваат најмалку 3 ѕидови (или повеќе). Кога ќе ги собереме аглите на тие ѕидови резултатот треба да биде помал од 360°. Бидејќи, ако резултатот е еднаков на 360° тогаш фигуратата е рамнина. Ѕидовите на правилен полиедар се идентични правилни многуаголници, па добиваме:
Формулата на Ојлер
За секој правилен полиедар важи: Резултатот од бројот на ѕидови плус бројот на темиња минус бројот на рабови
секогаш е еднаков на 2. Односно Ојлеровата теорема гласи:
F + V – E = 2
F = број на ѕидови
V = број на темиња
E = број на рабови
Да ја провериме нејзината точност за правилните полиедри.
Со помош на Ојлеровата теорема, може на друг начин да се покаќе дека има точно пет правилни полиедри. Доказот може да се најде во [2].
Постојат повеќе докази за докажување дека постојат само пет правилни полиедри. Еден од нив е со помош на големината на аглите кои се среќаваат во секое теме. Наједноставната причина зошто има само пет правилни полиедри е следнава:
Во секое теме мора да се среќаваат најмалку 3 ѕидови (или повеќе). Кога ќе ги собереме аглите на тие ѕидови резултатот треба да биде помал од 360°. Бидејќи, ако резултатот е еднаков на 360° тогаш фигуратата е рамнина. Ѕидовите на правилен полиедар се идентични правилни многуаголници, па добиваме:
- Правилен триаголник има агол од 60°, следува:
3 Триаголници (3 × 60° = 180°) – тетраедар
4 Триаголници (4 × 60° = 240°) – октаедар
5 Триаголници (5 × 60° = 300°) – икосаедар
6 Триаголници (6 × 60° = 360°) – рамнина - Правилен квадрат има агли од 90°, следува:
3 Квадрати (3 × 90° = 270°) – хексаедар т.е. коцка
4 Квадрати (4 × 90° = 360°) –рамнина - Правилен петаголник има агли од 108°, следува:
3 Петаголници (3 × 108° = 324°) – додекаедар
4 Петаголници (4 × 108° = 432°) – преголеми агли - Правилен шестаголник има агли од 120°, но 3 × 120° = 360° т.е. добиваме рамнина.
Формулата на Ојлер
За секој правилен полиедар важи: Резултатот од бројот на ѕидови плус бројот на темиња минус бројот на рабови
секогаш е еднаков на 2. Односно Ојлеровата теорема гласи:
F + V – E = 2
F = број на ѕидови
V = број на темиња
E = број на рабови
Да ја провериме нејзината точност за правилните полиедри.
- Тетраедар: 4 + 4 – 6 = 8 – 6 = 2
- Хексаедар: 6 + 8 – 12 = 14 – 12 = 2
- Октаедар: 8 + 6 – 12 = 14 – 12 = 2
- Додекаедар: 12 + 20 – 30 = 32 – 30 = 2
- Икосаедар: 20 +12 – 30 = 32 – 30 = 2
Со помош на Ојлеровата теорема, може на друг начин да се покаќе дека има точно пет правилни полиедри. Доказот може да се најде во [2].
Користена литература:
[1] Numberphile, 5 Platonic Solids, https://www.youtube.com/watch?v=gVzu1_12FUc
[2] Math is Fun, Platonic Solids - Why Five?, https://www.mathsisfun.com/geometry/platonic-solids-why-five.html
[3] Н. Целакоски, В. Бакева, Б. Миладиновиќ, Ј. Стефановски, Математика за втора година средно стручно образование за сите струки, МОН на РМ, 2010.
Автор:
Дамјан Зимбаков IX одд., ООУ Гоце Делчев, Босилово
Награден проект со трета награда на Ноември – Месец на науката 2019 во категорија 7-9 одд.
Професор:
Цвета Спасковска
Објавено на ПОИМ:
21 јануари 2020 година
Начин на цитирање на статијата:
Д. Зимбаков, Правилни полиедри - зошто пет?, Портал ПОИМ на Институтот за математика, ПМФ, Скопје, 21 јануари 2020 год., http://poim-pmf.weebly.com/pravilni-poliedri-zosto-pet.html
Авторизираните статии објавени на Порталот подлежат на законска заштита. Се забранува користење на статиите без наведување на авторот или изворот.
