НАУЧНО - ПОПУЛАРНИ СТАТИИСе залагаме за зголемување на свеста за местото и улогата на математиката во науките, технологијата, наставата, природата и културата.
|
НА ОПШТО ЗАДОВОЛСТВО: НОВ ТРЕНД ВО СТАТИСТИЧКИТЕ АНАЛИЗИ - ТЕСТОВИ ЗА ЕКВИВАЛЕНЦИЈА
(Оваа статија првично е објавена на порталот Наука за сите.)

Една од најважните карактеристики на добрата наука е нејзината непристрасност. Меѓутоа, константната потрага по разлики и супериорни резултати во однос на веќе постоечките, ја прави науката пристрасна и го оневозможува нејзиниот нормален развој.
Тестовите за еквиваленција се производи на статистичката теорија на заклучување кои интезивно се развиваат во последните години и кои овозможуваат подобро разбирање на функционирањето на реалниот свет, преку анализа на сличноста, а не на разликите ([1]). Во продолжение ќе се обидеме да ги објасниме овие тестови кои имаат моќ да ја отстранат пристрасноста на научните резултати, да го намалат бројот, па и да ги елиминираат неточно протолкуваните резултати и со тоа да предизвикаат експанзија на резултати од научните истражувања, „вадејќи ги од фиока“ досегашните „негативни резултати“.
При едно научно истражување основано на експерименти, единките на кои се однесува истражувањето на случаен начин се делат во две (а некогаш и повеќе) групи. Едната група е контролна, а другата е експериментална. На единките од експерименталната група се применува одредена интервенција (во медицинските истражувања тоа е нова терапија или нов лек, во инженерските истражувања може да биде нов метод итн.). Традиционално најчест облик на истражувачка хипотеза која се поставува е дека интервенцијата предизвикала разлика, а соодветната статистичка хипотеза која се тестира е хипотезата за непостоење на разлика. Доколку исходот од тестирањето е статистички значаен, статистичката хипотеза се отфрла и се потврдува истражувачката хипотеза, односно се потврдува дека интервенцијата предизвикала статистички значајна разлика на системот. Но, што се случува ако резултатот од тестирањето не е статистички значаен? Дали тоа значи дека интервенцијата е без влијание, нема ефект, дека е бескорисна? Еве едноставен пример од секојдневието. Вршиме тестирање на батерии со помош на батериска лампа. Ги ставаме батериите во лампата, ја вклучуваме лампата и ако таа свети заклучуваме дека батериите се добри. Ова е аналогно на изнаоѓање на статистички значајна разлика (по ставањето на батериите, лампата свети кога ќе се вклучи). Но, што ако не засвети лампата? Во овој случај никако не може да заклучиме дека батериите не се добри. Можно е батериската лампа да е расипана, можно е контактот со батериите да е слаб, можно е сијаличката да е прегорена или пак да не работи прекинувачот за вклучување или пак можеби неправилно сме ги ставиле батериите. Ова е аналогно на непостоење на статистички значајна разлика, односно не можеме да заклучиме дека постои разлика т.е. дека батериите се добри, што не значи дека не се добри. Заклучокот е: сите можности остануваат ([2]). Но, тоа што најчесто се случува при научните истражувања кога статистички значајна разлика не е најдена е за жал неточно толкување дека нема разлика, односно дека новата терапија нема ефект, па следствено научниот резултат е непосакуван и научните списанија не сакаат да го објават. Необјавен научен резултат, значи непризнаена терапија, па таа не може да се примени во пракса. Од друга страна, интезивниот развој на секое поле од науката значително ги има покачено стандардите, па изнаоѓање на нова терапија, нов лек или нов метод кој е супериорен во однос на веќе постоечките е сѐ потешко. А и неможноста да се открие статистички значајна разлика, може да биде показател и на недостаток на статистичката моќ на тестот да открие вистински ефект ([3]).
Пионерскиот обид на Ширман од 1987 година ([4]) и неговиот првопредложен статистички тест за еквиваленција TOST (two-one sided test), со кој наместо разлика се тестира еквиваленција, воведува нов начин на толкување на резултатите од експериментирањата. Од тогаш започнува развојот на статистичките тестови за еквиваленција кои овозможуваат прифаќање на нови терапии, лекови, методи со подобри секундарни карактеристики – помалку несакани последици, поевтини или поедноставни за користење, декларирајќи статистички значајна еквивалентност или пак отсуство на инфериорност. Развојот на овие тестови се должи и на неетичноста на користењето на плацебо ефектот при примена на супериорна терапија. Терминот еквивалентни не се користи во строга смисла, туку посочува на тоа дека ефектите се толку блиски, што не би можело да се каже која од двете терапии е супериорна или инфериорна. Овој концепт формално подразбира дефинирање на константа наречена маргина на еквивалентност δ со која се одредува опсегот на вредности за кои ефектите се „доволно блиски“ за да ги сметаме за еквивалентни. Во пракса, маргината на еквивалентност е максималната прифатлива разлика на примарните ефекти која сме подготвени да ја прифатиме за да ги добиеме секундарните придобивки од новата терапија. Дефинирањето на маргината на еквивалентност е најкритичниот момент при формирањето на тестот за еквивалентност. При мала вредост на маргината тешко се воспоставува статистички значајна еквивалентност, додека пак големи вредности на маргината може да го доведат во прашање кредибилитетот на истражувањето.
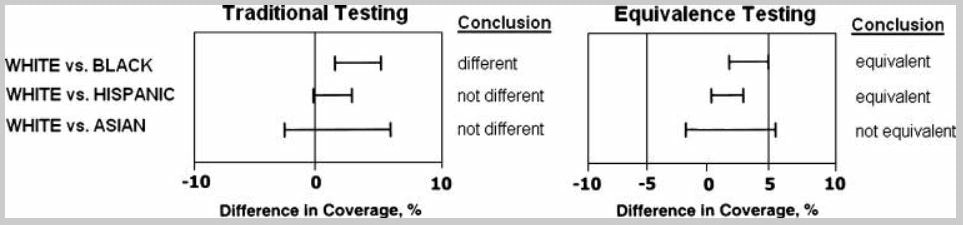
Да забележиме дека отсуството на статистички значајна разлика при користење на традиционалниот тест за разлика, не повлекува постоење на еквивалентност, од две причини, првата е дека станува збор за заклучоци од различни статистички тестови, а втората е непостоењето на маргина на еквивалентност што го прави концептот за еквивалентност бесмислен. Истражувањето на Баркер ([5]) за покриеност со вакцинација кај децата од различни етнички групи (црнци, шпанци и азијци) во споредба со истата кај белите деца (во улога на контролна група), убаво ја илустрира различната примена на овие два теста. Користејќи ниво на значајност α=0,05 за двата теста и маргина на еквивалентност δ од максимално дозволена 5 процентна разлика за TOST тестот, споредбата е направена со помош на 95% интервали на доверба добиени од првиот тест и 90% интервали на доверба добиени од вториот тест. Доколку 95% интервал на доверба од тестот за разлика не ја обфаќа нулата, велиме дека статистички значајна разлика е најдена, а ако 90% интервал на доверба од TOST тестот за еквиваленција е внатре во интервалот (-δ, δ) одреден со маргината на еквивалентност δ, велиме дека е откриена статистички значајна еквивалентност. Тестирана е покриеноста со седум вакцини, а анализата на покриеноста со MMR вакцината е прикажана на Слика 1. Според добиените резултати, традиционалниот тест за разлика има најдено статистички значајна разлика меѓу покриеноста со MMR вакцината кај црните во споредба со белите деца, но и TOST тестот има најдено статистички значајна еквивалентност на покриеноста со MMR вакцината кај овие две групи. Од друга страна, традиционалниот тест за разлика нема најдено статистички значајна разлика меѓу покриеноста со MMR вакцината кај шпанците во споредба со белите деца, додека TOST тестот има најдено статистички значајна еквивалентност. При споредба на покриеноста со MMR вакцината кај азијците во споредба со белите деца, и двата теста немаат најдено ниту статистички значајна разлика, ниту еквивалентност.
Тестовите за еквиваленција се производи на статистичката теорија на заклучување кои интезивно се развиваат во последните години и кои овозможуваат подобро разбирање на функционирањето на реалниот свет, преку анализа на сличноста, а не на разликите ([1]). Во продолжение ќе се обидеме да ги објасниме овие тестови кои имаат моќ да ја отстранат пристрасноста на научните резултати, да го намалат бројот, па и да ги елиминираат неточно протолкуваните резултати и со тоа да предизвикаат експанзија на резултати од научните истражувања, „вадејќи ги од фиока“ досегашните „негативни резултати“.
При едно научно истражување основано на експерименти, единките на кои се однесува истражувањето на случаен начин се делат во две (а некогаш и повеќе) групи. Едната група е контролна, а другата е експериментална. На единките од експерименталната група се применува одредена интервенција (во медицинските истражувања тоа е нова терапија или нов лек, во инженерските истражувања може да биде нов метод итн.). Традиционално најчест облик на истражувачка хипотеза која се поставува е дека интервенцијата предизвикала разлика, а соодветната статистичка хипотеза која се тестира е хипотезата за непостоење на разлика. Доколку исходот од тестирањето е статистички значаен, статистичката хипотеза се отфрла и се потврдува истражувачката хипотеза, односно се потврдува дека интервенцијата предизвикала статистички значајна разлика на системот. Но, што се случува ако резултатот од тестирањето не е статистички значаен? Дали тоа значи дека интервенцијата е без влијание, нема ефект, дека е бескорисна? Еве едноставен пример од секојдневието. Вршиме тестирање на батерии со помош на батериска лампа. Ги ставаме батериите во лампата, ја вклучуваме лампата и ако таа свети заклучуваме дека батериите се добри. Ова е аналогно на изнаоѓање на статистички значајна разлика (по ставањето на батериите, лампата свети кога ќе се вклучи). Но, што ако не засвети лампата? Во овој случај никако не може да заклучиме дека батериите не се добри. Можно е батериската лампа да е расипана, можно е контактот со батериите да е слаб, можно е сијаличката да е прегорена или пак да не работи прекинувачот за вклучување или пак можеби неправилно сме ги ставиле батериите. Ова е аналогно на непостоење на статистички значајна разлика, односно не можеме да заклучиме дека постои разлика т.е. дека батериите се добри, што не значи дека не се добри. Заклучокот е: сите можности остануваат ([2]). Но, тоа што најчесто се случува при научните истражувања кога статистички значајна разлика не е најдена е за жал неточно толкување дека нема разлика, односно дека новата терапија нема ефект, па следствено научниот резултат е непосакуван и научните списанија не сакаат да го објават. Необјавен научен резултат, значи непризнаена терапија, па таа не може да се примени во пракса. Од друга страна, интезивниот развој на секое поле од науката значително ги има покачено стандардите, па изнаоѓање на нова терапија, нов лек или нов метод кој е супериорен во однос на веќе постоечките е сѐ потешко. А и неможноста да се открие статистички значајна разлика, може да биде показател и на недостаток на статистичката моќ на тестот да открие вистински ефект ([3]).
Пионерскиот обид на Ширман од 1987 година ([4]) и неговиот првопредложен статистички тест за еквиваленција TOST (two-one sided test), со кој наместо разлика се тестира еквиваленција, воведува нов начин на толкување на резултатите од експериментирањата. Од тогаш започнува развојот на статистичките тестови за еквиваленција кои овозможуваат прифаќање на нови терапии, лекови, методи со подобри секундарни карактеристики – помалку несакани последици, поевтини или поедноставни за користење, декларирајќи статистички значајна еквивалентност или пак отсуство на инфериорност. Развојот на овие тестови се должи и на неетичноста на користењето на плацебо ефектот при примена на супериорна терапија. Терминот еквивалентни не се користи во строга смисла, туку посочува на тоа дека ефектите се толку блиски, што не би можело да се каже која од двете терапии е супериорна или инфериорна. Овој концепт формално подразбира дефинирање на константа наречена маргина на еквивалентност δ со која се одредува опсегот на вредности за кои ефектите се „доволно блиски“ за да ги сметаме за еквивалентни. Во пракса, маргината на еквивалентност е максималната прифатлива разлика на примарните ефекти која сме подготвени да ја прифатиме за да ги добиеме секундарните придобивки од новата терапија. Дефинирањето на маргината на еквивалентност е најкритичниот момент при формирањето на тестот за еквивалентност. При мала вредост на маргината тешко се воспоставува статистички значајна еквивалентност, додека пак големи вредности на маргината може да го доведат во прашање кредибилитетот на истражувањето.
Да забележиме дека отсуството на статистички значајна разлика при користење на традиционалниот тест за разлика, не повлекува постоење на еквивалентност, од две причини, првата е дека станува збор за заклучоци од различни статистички тестови, а втората е непостоењето на маргина на еквивалентност што го прави концептот за еквивалентност бесмислен. Истражувањето на Баркер ([5]) за покриеност со вакцинација кај децата од различни етнички групи (црнци, шпанци и азијци) во споредба со истата кај белите деца (во улога на контролна група), убаво ја илустрира различната примена на овие два теста. Користејќи ниво на значајност α=0,05 за двата теста и маргина на еквивалентност δ од максимално дозволена 5 процентна разлика за TOST тестот, споредбата е направена со помош на 95% интервали на доверба добиени од првиот тест и 90% интервали на доверба добиени од вториот тест. Доколку 95% интервал на доверба од тестот за разлика не ја обфаќа нулата, велиме дека статистички значајна разлика е најдена, а ако 90% интервал на доверба од TOST тестот за еквиваленција е внатре во интервалот (-δ, δ) одреден со маргината на еквивалентност δ, велиме дека е откриена статистички значајна еквивалентност. Тестирана е покриеноста со седум вакцини, а анализата на покриеноста со MMR вакцината е прикажана на Слика 1. Според добиените резултати, традиционалниот тест за разлика има најдено статистички значајна разлика меѓу покриеноста со MMR вакцината кај црните во споредба со белите деца, но и TOST тестот има најдено статистички значајна еквивалентност на покриеноста со MMR вакцината кај овие две групи. Од друга страна, традиционалниот тест за разлика нема најдено статистички значајна разлика меѓу покриеноста со MMR вакцината кај шпанците во споредба со белите деца, додека TOST тестот има најдено статистички значајна еквивалентност. При споредба на покриеноста со MMR вакцината кај азијците во споредба со белите деца, и двата теста немаат најдено ниту статистички значајна разлика, ниту еквивалентност.
Слика 1. Резултати добиени со традиционалниот тест за разлики и тестот за еквивалентност (TOST) со маргина δ=5% за споредбата на покриеност со MMR вакцината кај белите деца и децата од различни етнички групи (црнци, шпанци и азијци). Отсуството на статистички значајна разлика, може, но и не мора да значи постоење на еквивалентност. ([1])
Заради непристрасноста на науката, сосема природно се наметнува оддалечувањето од тестовите за разлика и сѐ поголема примена на тестирање на сличноста. Иако првопредложениот тест за еквиваленција е од пред околу три децении, заради спориот процес на разбирање на една теорија, што е предуслов за нејзина имплементација, како и нејзиниот постојан развој, придобивките од примената на тестовите за еквиваленција до првин ќе ги гледаме.
Поважни термини и ознаки:
Статистички значаен – резултатот е статистички значаен ако p-вредноста е помала од нивото на значајност α. Повеќе за статистичкото заклучување при тестирање на статистички хипотези може да прочитате во статијата „Статистичко заклучување - врската меѓу теоријата и експериментот“.
δ (делта) – маргина на еквивалентност т.е. дозволената максимална разлика меѓу старата и новата терапија за да ги сметаме терапиите за еквивалентни.
Интервал на доверба – интервал со кој се оценува вредноста на некој непознат параметар, така 95% интервал на доверба означува дека постојат 95% шанси да тој интервал ја содржи вистинската вредност на оценуваниот параметар.
Извори:
[1] E. Walker, A. S. Nowacki, Understanding Equivalence and Noninferiority Testing, J Gen Intern Med. 2011 Feb; 26(2): 192–96, https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3019319/
[2] What it means when “no significant differences were found” | PurposeResearch.com,
http://purposeresearch.com/wdprs/2012/04/what-it-means-when-no-significant-differences-were-found/
[3] D. Lakens, Equivalence Tests: A Practical Primer for t Tests, Correlations, and Meta-Analyses, Soc Psychol Personal Sci. 2017 May; 8(4):355-362, https://journals.sagepub.com/doi/pdf/10.1177/1948550617697177
[4] D. J. Schuirmann, A comparison of the two one-sided tests procedure and the power approach for assessing the equivalence of average bioavailability, Journal of Pharmacokinetics and Biopharmaceutics 15 (1987), 657–680.
[5] Barker LE, Luman ET, McCauley MM, Chu SY. Accessing equivalence: an alternative to the use of difference tests for measuring disparities in vaccination coverage. Am J Epidemiol. 2002;156:1056–1061.
Автор:
Ирена Стојковска, Институт за математика, Природно-математички факултет, Скопје
Објавено на ПОИМ:
21 март 2020
Начин на цитирање на статијата:
И. Стојковска, На општо задоволство: Нов тренд во статистичките анализи - тестови за еквиваленција, Портал ПОИМ на Институтот за математика, ПМФ, Скопје, хх мај 2019, http://poim-pmf.weebly.com/nov-trend-vo-statistickite-analizi-testovi-za-ekvivalencija.html
Download (PDF)
Авторизираните статии објавени на Порталот подлежат на законска заштита. Се забранува користење на статиите без наведување на авторот или изворот.