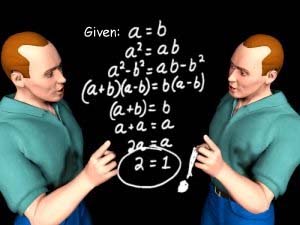3 / 4
|
Улогата, примената и важноста на туторството во образованието на 21 век (PDF)
3 декември 2021 во МАТЕМАТИЧКИ ОМНИБУС (НАСТАВА) Ќе зборуваме за туторството во рамките на формалното образование, коешто е присутно од предучилишната возраст до високото образование. Иако скоро секој образован возрасен човек може да му помогне на ученик од пониските одделенија на основното образование во вежбање читање и говор, броење или основна математика, со голема доза на стрпливост при објаснувањето, сепак, постојат области каде што се потребни посебни стручни познавања, искуство и континуирана надградба на туторот за ефективна работа. Активностите во воспитно-образовниот процес, треба да бидат такви што пред сѐ ќе ги создадат потребните предуслови ученикот да се развие во отворена, самостојна, креативна и карактерна личност, во согласност со неговите развојни потреби и интереси, a училиштето да стане место за социјализација на учениците и привлечна средина за учење. Во дидактичкo-методските техники за оваа намена, на високо позиционирано место сигурно ќе се најде соученичкото туторство, од кое резултатите се повеќе од очигледни. Труд објавен во Математички омнибус 10 (2021). |
|
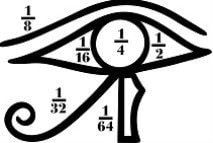
Египетски дропки (PDF)
4 ноември 2021 во МАТЕМАТИЧКИ ОМНИБУС (НАСТАВА) Сте се запрашале ли како Египќаните ги запишувале броевите? А, како пак ги запишувале дропките? Од друга страна, навидум две далечни прашања: дали збирот на две различни дропки со броител 1 и именител позитивен цел број, (кои ќе ги нарекуваме единични дропки) е секогаш единична дропка? Дали е можно секоја единична дропка да ја претставиме во вид на збир од две единични дропки? Каква е врската помеѓу првиот пар прашања и вториот пар прашања? Нашите сознанија за египетската математика се должат во голема мера на два египетски папируса. Едниот е Рајндовиот папирус, а вториот е Moсковскиот папирус. Ќе се осврнеме на Рајндовиот папирус, на алгоритмот на Фибоначи, на бесконечни претставувања и на примената во наставата. Труд објавен во Математички омнибус 10 (2021). |
|
(Не)Возможна ослободителна стратегија
3 ноември 2021 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Математичките загатки отсекогаш привлекувале големо внимание кај секој од нас. Многу често на прв поглед тие изгледаат нерешливи, конфузни и многу комплицирани. Многу често имаме случаи во кои нашата цел не е решавање на загатката, туку разбирање на решението на загатката. Исто така, не се ретки случаите во кои врз база на даденото решение на една загатка, се обидуваме да најдеме нејзино поелегантно решение. Една таква загатка е и загатката позната под името 100 затвореници, која за прв пат била дадена во 2003 година од страна на данскиот компјутерски научник Питер Бро Милтерсен. Како што кажува и самото име на оваа загатка, станува збор за затвореници чија крајна цел е да добијат ослободителна пресуда, односно да ја победат управата на затворот во играта која се игра под одредени правила. Овој проблем е поставен во многу различни верзии, но секоја од нив ја има истата цел. Во продолжение ќе наведеме две познати верзии на овој проблем. Прво ќе ја наведеме првичната формулација на проблемот, а потоа верзијата во која најчесто се среќава овој проблем, т.е. формулацијата како загатка. Труд објавен во Математички омнибус 9 (2021). |
|
Фибоначиевите броеви, теоријата на Елиот и тргувањето со хартии од вредност
25 октомври 2021 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Познато е дека Фибоначиевите броеви се појавуваат во математиката, посебно во геометријата при изучувањето на златниот пресек, како и кај разни „златни“ фигури, потоа кај Паскаловиот триаголник, но се појавуваат и на некои многу необични места: во природата, во архитектурата, во музичките форми и во економијата, посебно кај финансиските пазари. Финансиските пазари можат да се опишат како бикови или мечки. Биковите (анг. Bull markets) имаат растечка вредност на акциите и стабилна економија, додека кај мечките (анг. Bear markets) вредноста на акциите опаѓа и економијата е во рецесија. Интересно е тоа што ваквите пазари често сами себе се засилуваат поради тоа што исто така ги претставуваат мислите и очекувањата на инвеститорите. Да видиме како сето ова има врска со Фибоначиевите броеви. Елиот забележал дека пазарите мечки се состојат од 2 импулсивни бранови и 1 корективен бран, притоа формирајќи вкупно 3 бранови. Исто така, пазар бик се состои од 3 импулсивни, па 2 корективни бранови, со што се добиваат вкупно 5 бранови. Целосен пазарен циклус би бил комбинација од сите овие движења, односно би се состоел од 8 бранови... Труд објавен во Математички омнибус 9 (2021). |
|
Идентитетот на троен производ на Јакоби
21 октомври 2021 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Во овој труд се презентира едноставен елементарен доказ на идентитетот на троен производ на Карл Густав Јакоби (1804-1851), кој претставува централен резултат во теоријата на елиптични функции. За соодветни вредности на 𝑞 и 𝑧, се добиваат класични идентитети познати од аналтичката теорија на броеви. Доказот е според презентацијата во книгата Квантна анализа (Quantum calculus) на Виктор Кац, која се заснова на теоријата на 𝑞 − редови. Ги даваме дефинициите на 𝑞 −дифернцијали и 𝑞 − биномни коефициенти и ги презентираме нивните основни својства. Од овие теореми на 𝑞 −анализа се изведуваат класичните биномни формули на Гаус и Хајне. Од нив, преку прост процес на определување гранична вредност, ќе се добијат познатите идентитети на Ојлер за 𝑞 − редови со бесконечно многу суманди. Труд објавен во Математички омнибус 9 (2021). |
|
Пандемиски игри и стратегии (PDF)
30 септември 2021 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Светот е исправен пред предизвиците на првата сериозна пандемија во вистински глобално поврзан свет. Најдени во една состојба на неизвесност, со многу непознати и неодговорени прашања, поединци, групи и глобални субјекти се обидуваат да ги најдат потребните одговори и да ги применат неопходните мерки. Не е тешко да разбереме дека преземените дејства подразбираат комплексна организација и координација на неколку нивоа. Државите, областите и регионите се налик на сврзани садови и ако некој од нив ја загуби контролата над ситуацијата, опасноста ќе се пренесе на други места. Така, богатите и развиени земји сфаќаат дека индивидуалните напори не се доволни и дека една навидум стабилна состојба може бргу да се влоши ако се појават сериозни епидемии во соседството, во неразвиени земји или области, или пак во случај на интензивна сообраќајна размена со ризични подрачја. Ова подразбира дека е потребна соработка (кооперативност) и не само координација за решавање на настанатите проблеми. Среде една, наизглед хаотична ситуација, и науката се обидува да помогне и да одговори на дел од прашањата. Но тоа не е воопшто лесно, земајќи предвид дека сериозните пандемии се ретки настани и едноставно нема доволно податоци од кои ќе се извлечат статистички значајни заклучоци. Труд објавен во Математички омнибус 9 (2021). |
|
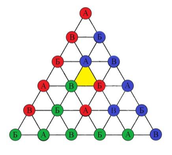
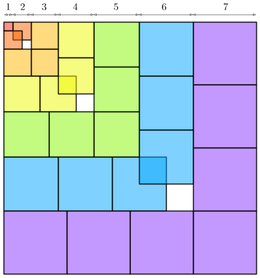
Што е заедничко за мешање чај во шолја, боење темиња во триаголник и фер поделба на трошоци за станарина? (PDF)
29 септември 2021 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Колку добро може да измешаме чај во една шолја? Дали со таканаречено идеално мешање само во круг и без протресување на шолјата може да ја измешаме течноста толку добро, што по нејзиното сталожување сите молекули ќе бидат разместени во положба различна од почетната? Одговорот на ова прашање е негативен. Ако честичките чај во чашата ги сметаме за точки, тогаш (со занемарлива грешка) по секое мешање барем една молекула ќе се врати во почетната положба од којашто почнала да се движи. Овој заклучок му се припишува на холандскиот математичар Брауер (L. E. J. Brouwer). Тој ја формулирал и докажал познатата Tеорема на Брауер за неподвижна точка, од којашто директно следува заклучокот. Оваа теоремата заради едноставноста, и покрај тополошката природа, наоѓа примена во многу различни, па дури и неочекувани области, како што се економијата и теоријата на игри. Дел од заслугата за тоа имаат разните дополнувања на оваа теорема, како и тврдењата еквивалентни на неа. Интересен еквивалент на теоремата на Брауер од аспект на комбинаториката е Шпернеровата лема. Труд објавен во Математички омнибус 9 (2021). |
|
Декомпозиција на матрица на сингуларни вредности, анализа на нејзината временска и просторна сложеност и примена при компресија на слики (PDF)
6 септември 2021 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Идејата зад декомпозицијата на матрица на сингуларни вредности лежи во обопштувањето на спектралната декомпозиција или уште позната како факторизација со сопствени вредности којашто се изведува кај квадратните матрици. Декомпозицијата на матрица на сингуларни вредности има прилично долга историја, со тоа што првпат овој метод бил разгледуван од страна на математичарите во доцниот XIX век. Но, важните примени на оваа техника почекале сѐ додека пресметковната моќ на компјутерите не станала достапна во втората половина на XX век, кога биле развиени различни алгоритми за нејзина ефикасна имплементација. Во овој труд e претставена практичната примена на декомпозицијата на сингуларни вредности при компресија на дигитални слики, односно намалување на меморискиот капацитет којшто е потребен за нивно чување. Секако, треба да сме свесни дека SVD (Singular Value Decomposition) претставува компромис меѓу посакуваниот степен на компресија кој сакаме да го постигнеме и задржувањето на прифатлив квалитет на сликата, која нема да отстапува многу од оригиналот. Исто така, се соочивме со предизвици при преминот од теорија во пракса, при што ги искористивме знаењата од линеарна алгебра за да ја намалиме временската сложеност на овој алгоритам. На крајот, беше покажано дека со мала модификација на постапката, истиот метод може да се употреби за компресија и на црно-бели и на слики во боја. Труд објавен во Математички омнибус 9 (2021). |
|
Критериуми за избор и начини на комбинирање дигитални и аналогни ресурси во наставата по математика (PDF)
28 јуни 2021 во МАТЕМАТИЧКИ ОМНИБУС (НАСТАВА) Како и другите традиционални алатки кои се карактеристични за наставата по математика, на пример линијар и шестар, така и дигиталните технологии имаат значајна улога во нејзината реализација. Валидноста за примена на иновативни дигитални технологии во наставата по математика не се состои во замена или во исфрлање на традиционалните алатки, туку напротив, во нивно дополнување и отворање на нови можности за учениците. Сепак, бројноста и разновидноста на дигиталните алатки кои се слободно достапни на интернет може да предизвика збунетост или потешкотии при нивниот правилен избор. Кои дигитални алатки имаат доволно квалитет, во што точно се состои нивниот квалитет, како да се комбинираат неколку алатки за време на еден наставен час, итн. се само дел од прашањата кои заслужуваат научно-истражувачко внимание и темелен пристап. Труд објавен во Математички омнибус 10 (2021). |
|
Одлучувањето на младата популација во доменот на личните финансии: повеќекритериумски пристап (PDF)
30 јуни 2021 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Како едно од најбрзо растечките полиња на дисциплината операциони истражувања, повеќекритериумското одлучување се однесува на донесување одлука во услови на голем број критериуми кои можат да бидат меѓусебно конфликтни. Повеќекритериумското одлучување забележува огромна примена во последните неколку децении, во донесувањето одлуки во секојдневниот живот, но и во голем број други области: бизнис, образование, политика, медицина, животна средина, енергетика, спорт и др. Во процесот на одлучување во доменот на личните финансии постојат конфликтни критериуми при избирање на соодветната финансиска опција, особено кога се има предвид односот ризик – принос. Идеалната комбинација би била остварување на високи приноси, истовремено минимизирајќи ги ризиците, иако, во реалноста, средствата што имaат потенцијал да остварат високи приноси, обично носат и високи ризици. При одлучувањето во ситуации од секојдневниот живот, луѓето вообичаено донесуваат одлуки врз основа на интуиција. Од друга страна, за посложени проблеми, особено за оние што вклучуваат финансиска компонента, важно е проблемот да се структурира и да се вклучат повеќе критериуми во анализата. Труд објавен во Математички омнибус 9 (2021). |
|
Користење на матрична факторизација во системи за препорачување (PDF)
29 јуни 2021 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Под систем за препорачување се подразбира систем кој тежи да ја предвиди оцената или преферирањето на одреден објект од страна на специфичен корисник. Последните години ваков тип системи се неизбежен дел од платформите кои се трудат да го погодат вкусот на своите корисници и да им ги понудат оние производи или содржини кои ним најмногу би им се допаднале. Најпознат пример за ваков систем е платформата Нетфликс (Netflix) која врши селекција на филмови и серии кои би им се допаднале на нивните корисници. Ваквите системи добија најголема популарност кога оваа компанија го објави познатиот натпревар “The Netflix Prize”, во кој понудија еден милион долари на оној кој ќе го подобри постоечкиот систем за препораки за 10%. Во овој труд е анализирано решението кое победи на натпреварот, кое се базира на факторизација на матрици, односно запишување на матрицата од веќе дадени оцени, како производ од две други матрици. Труд објавен во Математички омнибус 9 (2021). |
|
Некои недостатоци во учебниците по математика за основно образование по адаптираната наставна програма од 2015 и 2016 година за темата броеви (PDF)
26 јуни 2021 во МАТЕМАТИЧКИ ОМНИБУС (НАСТАВА) За еден ученик да ја засака математиката и да ја работи во понатамошното образование, потребно е да има добар темел кој се гради во основното образование. Во градењето на овој темел, покрај талентот на поединицот огромна улога имаат наставникот и учебникот. Наставникот како стручен кадар има задача соодветната наставна материја прецизно да ја пренесе на наједноставен и прифатлив начин на учениците. Но, бидејќи секој ученик различно го прима пренесувањето од наставникот, многу е важно и учебникот да биде добар, концизен, јасен и секако адаптиран на нивото на самите ученици. Како резултат на недостатоци во некои од учебниците, се појавуваат одредени дилеми и збунетост кај голем дел од учениците, па дури и кај оние кои се талентирани за математика. Кај дел од нив, тие се провлекуваат и во понатамошното нивно образование. Труд објавен во Математички омнибус 10 (2021). |
|
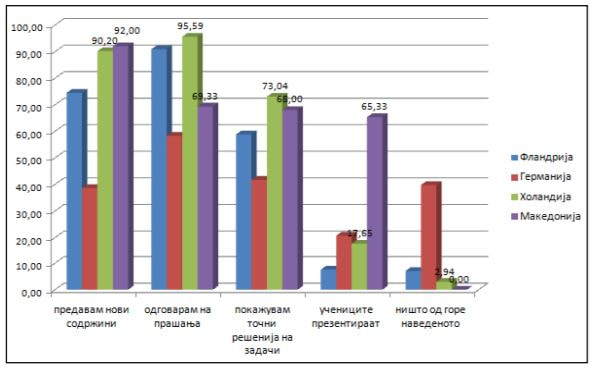
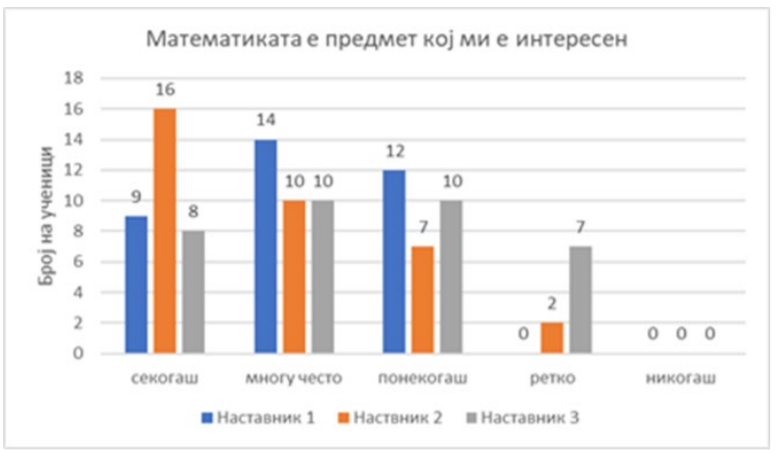
Kористење на дигитални алатки во наставата по математика пред и за време на кризата со пандемија (PDF)
4 јуни 2021 во МАТЕМАТИЧКИ ОМНИБУС (НАСТАВА) Математичко образование кое е динамично и адаптибилно на реалните животни ситуации може да ги промовира вредноста и значењето на математиката во општеството. Овој труд има цел да ги прикаже добиените резултати од спроведено емпириско истражување кое се однесува на предметната настава со учење на далечина по математика во основните училишта во Македонија пред и за време на кризата со пандемијата во 2020 година. Истражувањето нуди реална слика за наставните практики при користење на дигитални алатки од страна на наставниците по математика во земјата како би можело да се овозможи понатамошно планирање и усовршување според нивните потреби. Понатаму, направена е и споредба со резултати од слични научни истражувања надвор од земјата, во конкретниов случај со Сојузна Република Германија и Кралството Холандија. Труд објавен во Математички омнибус 10 (2021). |
|
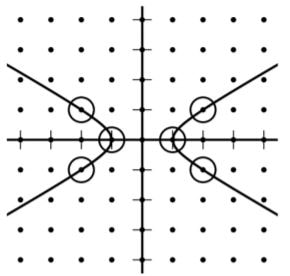
Модел на онлајн наставен час променет во настава по математика во основно образование (PDF)
3 јуни 2021 во МАТЕМАТИЧКИ ОМНИБУС (НАСТАВА) Целта на овој труд е да прикаже модел за реализација на наставен час со активности во три дела (активности пред часот-асинхрони, активности за време на часот-синхрони и активности по часот-асинхрони) со користење интерактивни дигитални ресурси, кој е базиран на чекорите во математичкиот процес за решавање проблеми според рамката на PISA21 (Programme for International Student Assessment). Прикажаниот модел се однесува на цели од наставната програма за IX одделение од темата Алгебра и решавање проблеми, а очекуваниот исход е учениците да ја „откријат“ Пиковата теорема. Труд објавен во Математички омнибус 10 (2021). |
|
Предностите и предизвиците на наставата по математика од далечина во услови на пандемија (PDF)
2 јуни 2021 во МАТЕМАТИЧКИ ОМНИБУС (НАСТАВА) Како во многу земји, така и кај нас борбата против КОВИД-19 ja попречи редовната настава во училиштата и нормалното вообичаено живеење воопшто. За да се унапреди самот процес на online поучување, со цел постигнување повисоки резултати, трајни и применливи знаења, го спроведовме ова истражување воопштено, а потоа и конкретно за математиката како наставен предмет, којашто игра клучна улога во развојот на критичкото мислење на учениците и нивниот понатамошен професионален развој. Целта на истражувањето е да се изведат заклучоци за квалитетот на реализацијата на online наставата, како и да се добијат насоки за нејзино унапредување. Труд објавен во Математички омнибус 10 (2021). |
|
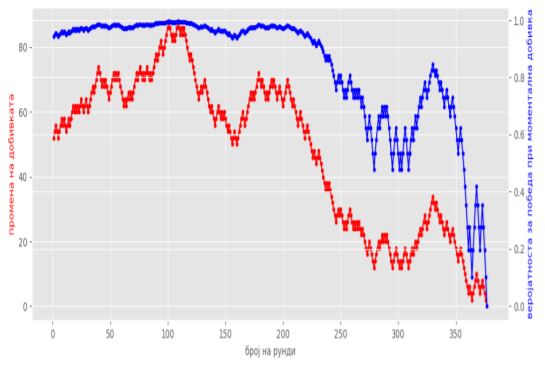
Бриеровиот скор и предвидувачките турнири (PDF)
6 декември 2020 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Неизвесноста на идните настани и желбата да се знае што ќе се случи, кај секого буди интерес за предвидување. Интересот е помасовен, ако исходите од тие настани имаат глобално значење. „Колку случаи на заболени од COVID-19 ќе бидат регистрирани до 1 април 2021 година?“ е само едно од прашањата од глобален интерес во моментот на издавањето на овој труд. Слични актуелни прашања за настани во блиска иднина се поставуваат на предвидувачките турнири на кои индивидуалци или тимови се обидуваат да дадат веројатносна проценка за нивна реализација. Победник на предвидувачкиот турнир е тимот кој има најголема предвидувачка способност, која пак се мери со помош на Бриеровиот скор. Труд објавен во Математички омнибус 7 (2020). |
|
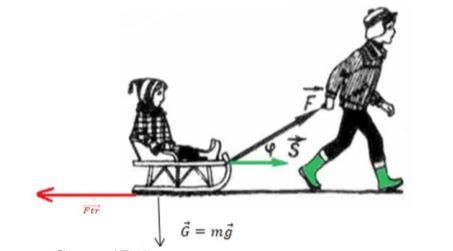
Математичка физика или физичка математика на часовите по физика и математика во средното образование (PDF)
6 ноември 2020 во МАТЕМАТИЧКИ ОМНИБУС (НАСТАВА) Неизбежен е фактот дека знаењето на математика е еден од важните предуслови при решавањето на задачи во природните науки, па и во тој контекст на решавање на задачи по физика. Од друга страна, пак, математиката е нејасен, неразбирлив дијалект, без конкретно значење на x и y во повеќе релации и формули. Тој „неразбирлив дијалект“ понекогаш е пречка за поголем број ученици. Така, од нешто што е релативно едноставно („лесно“) во физиката, со непознавање на математичкиот апарат, на одредена возраст станува релативно комплицирано („тешко“), односно пречка за разбирање на одредени содржини. Труд објавен во Математички омнибус 8 (2020). |
|
Демографските промени низ призмата на математичките модели (PDF)
2 септември 2020 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Уште во 17-тиот век, Џон Гронт (John Graunt, 1620 – 1674), ги поставил основите на демографијата како наука, истражувајќи ги неделните статистики на смртни случаи и крштевања во Лондон. Во 18-тиот век, оваа навидум општествена дисциплина, ја покажува својата интердисциплинарност, дел од научниот свет ја препознава како феномен со статистички правилности. Влечејќи информации од економијата, социологијата, статистиката, медицината, биологијата, антропологијата и историјата, демографијата станува основа за планирањето и општествен развој. Нашата идеја овде е да укажеме на важноста и примената на математичките модели без кои проекциите на населението и анализата на индексните стапки на смртност, новородени, фертилитет, миграција не би биле возможни. Труд објавен во Математички омнибус 7 (2020). |
|
Математиката и правото
21 август 2020 СТАТИИ ЗА НАСТАВАТА ПО МАТЕМАТИКА Потрагата по вистината и нејзиното докажување е заеднички предизвик за математиката и правото. Во математиката, основните поими и аксиоми се темел на изведените тврдења. Секоја друга вистина е во согласност со другите, добиена по пат на логичко заклучување. Дали уредниот и сеопфтен доказ кој математичарите сакаат да го прочитаат за да бидат убедени во кажувањето на теоремите е завршниот говор на правните случаи кон којшто целат адвокатите? Download (PDF) |
|
Феноменот „Пропаст на коцкарот“ и случајното талкање (PDF)
20 август 2020 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Во последната деценија, коцкањето стана една од најпосакуваните „занимации“ ширум светот. Дел од луѓето кои се искусни во практикување на таа активност, вложуваат пари со надеж дека ќе добијат многу повеќе. Постојат и такви кои „пробуваат само еднаш“, а со самото тоа, свесно или несвесно, се доведуваат до работ да изгубат сè, т.е. до таканаречената пропаст на коцкарот. Во овој труд се презентирани генералните заклучоци добиени за коцкарот кој се обидел со постојано вложување (обложување) да освои максимални € N без да доживее коцкарска пропаст. Дали може да успее? Колкава е веројатноста да успее? И кое е очекуваното времетраење на една коцкарска игра до постигнување на посакуваната добивка или до коцкарската пропаст? Труд објавен во Математички омнибус 7 (2020). |
|
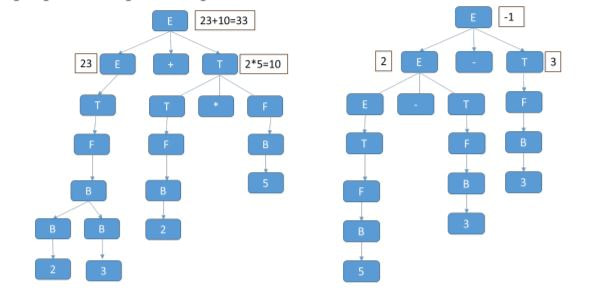
Формални граматики и нивна примена во дизајн на програмски јазици (PDF)
4 август 2020 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Формалните граматики несомнено претставуваат револуционен изум кој довел до развој на компјутерските науки, посебно развојот на програмските јазици како средство за комуникација помеѓу човекот и машината. Овој труд ја прикажува логичката страна, односно математичкиот концепт, за конструкција на една таква граматика. Разработката е направена преку илустрација на градењето на една од најосновните граматики, граматиката за формирање на правилни математички изрази, која е подмножество на секоја граматика за програмски јазик. Труд објавен во Математички омнибус 7 (2020). |
|
Игрите Еренфојт-Фрајсе: за логичките искази и строгите докази (PDF)
14 јули 2020 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Теоријата на игри е полна со длабоки загатки, кои се извор на чести несогласувања околу предложените решенија. Логичкиот пристап при решавање на ови проблеми се чини најсоодветен бидејќи се однесува директно на размислувањето, знаењето и спротиставеноста, како и поради неговата функција во утврдување на валидноста на аргументите. Игрите Еренфојт – Фрајсе се меѓу малкуте методи кои може да се применат кај конечните структури, а со тоа и во многубројни проблеми од компјутерската наука. Нивната примена е погодна и транспарентна кај релациони структури со унарни и бинарни релации, како што се графовите, линеарните и делумните подредувања, кои доминираат во многу области од компјутерската наука. Овие игри може да бидат интересни и за љубителите на креативни, но ригорозни математички докази. Труд објавен во Математички омнибус 7 (2020). |
|
Стандарди за оценување низ призма на задачи за алгебарски дропки (PDF)
29 мај 2020 во МАТЕМАТИЧКИ ОМНИБУС (НАСТАВА) Кога станува збор за наставата по математика, наставните цели треба да бидат така формулирани, што лесно ќе може да се измери дали една наставна цел е или не е исполнета. Oбразовните стандарди даваат одговор на прашањето: До кое ниво, основно или напредно, ученикот мора да има усвоени знаења, развиени вештини и ставови за успешно да го заврши образовниот процес во рамки на своето формално образование? Целта на ова истражување е да се разгледаат стандардите и критериумите на оценување преку споредба на решавањето на ист тест во две различни училишта. Труд објавен во Математички омнибус 8 (2020). |
|
Математички хепенинг „Ден на бројот ПИ“ (PDF)
25 мај 2020 во МАТЕМАТИЧКИ ОМНИБУС (НАСТАВА) Знаеме дека кај учениците постои страв од математиката, верување дека математикатa е тешка, непотребна и несовладлива за повеќето ученици и привилегија за само некои ученици кои можат да ја научат. Добар дел од родителите го споделуваат тој став со своите деца, со што тие губат интерес за предметот. Затоа еден од најголемите предизвици за наставниците по математика е кај учениците да ја разбудат желбата за учење математика и љубовта кон математиката. Труд објавен во Математички омнибус 8 (2020). |
|
Професионалниот развој и работното искуство на наставникот како фактори за успешно реализирана настава (PDF)
24 мај 2020 во МАТЕМАТИЧКИ ОМНИБУС (НАСТАВА) Еден од клучните фактори за квалитет на наставниот процес, поконкретно на квалитетната настава е самиот предавач – наставникот. Наставникот треба да е добар пример на своите ученици, од кои очекуваме да го следат, оценат, па дури потсвесно да го ископираат предложениот модел. За да се унапреди самот процес на поучување, со цел постигнување повисоки резултати, трајни и применливи знаења, наставникот треба да е и самиот „ученик“ во целиот свој професионален животен пат, односно треба да има континуиран професионален развој. Труд објавен во Математички омнибус 8 (2020). |
|
Математика за економисти - трајни недостатоци, конфузии и енигми (PDF)
22 мај 2020 во МАТЕМАТИЧКИ ОМНИБУС (НАСТАВА) Прецизноста во математичките пресметки е мост кој ги поврзува практичните проблеми и правилниот пристап кон тие практични проблеми од нашето секојдневие. Понекогаш, грешките во математичките пресметки при решавање на некој практичен проблем може дури и да се занемарат, доколку последиците од нив не се впечатливи. Но, она што не смее да отсуствува, а практично, е и механизам да се справиме со грешките при решавањето задачи е толкувањето. Труд објавен во Математички омнибус 8 (2020). |
|
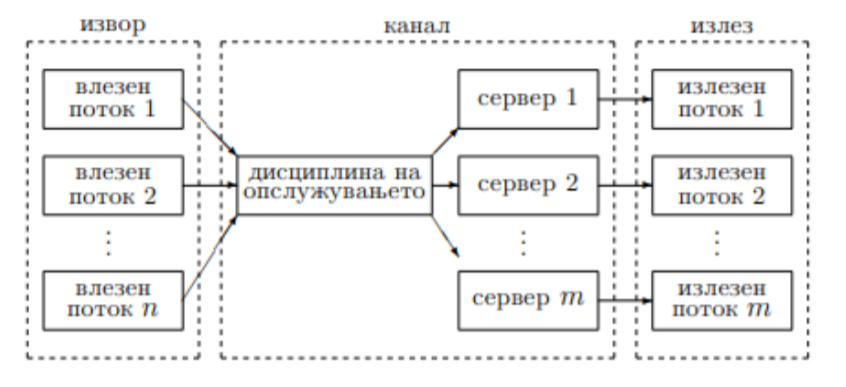
Техники за генерирање случајни променливи во системи за масовно опслужување од типот M/M/n (PDF)
30 април 2020 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Теоријата на масовно опслужување е област во која се конструирани математички модели со чија помош може да се регулираат масовните појави од секојдневието. Имено, оваа област ни нуди можност да се справиме со редиците на чекање кои настануваат во банките, продавниците, бензинските пумпи, но и во централите до кои пристигнуваат некакви сигнали, итн. Едни од поедноставните модели на масовно опслужување се оние со Пoасонов влезен поток и експоненцијално време на опслужување. Со техниките за генерирање на случајните променливи од овие системи се обезбедува подобро разбирање на системите. Труд објавен во Математички омнибус 7 (2020). |
|
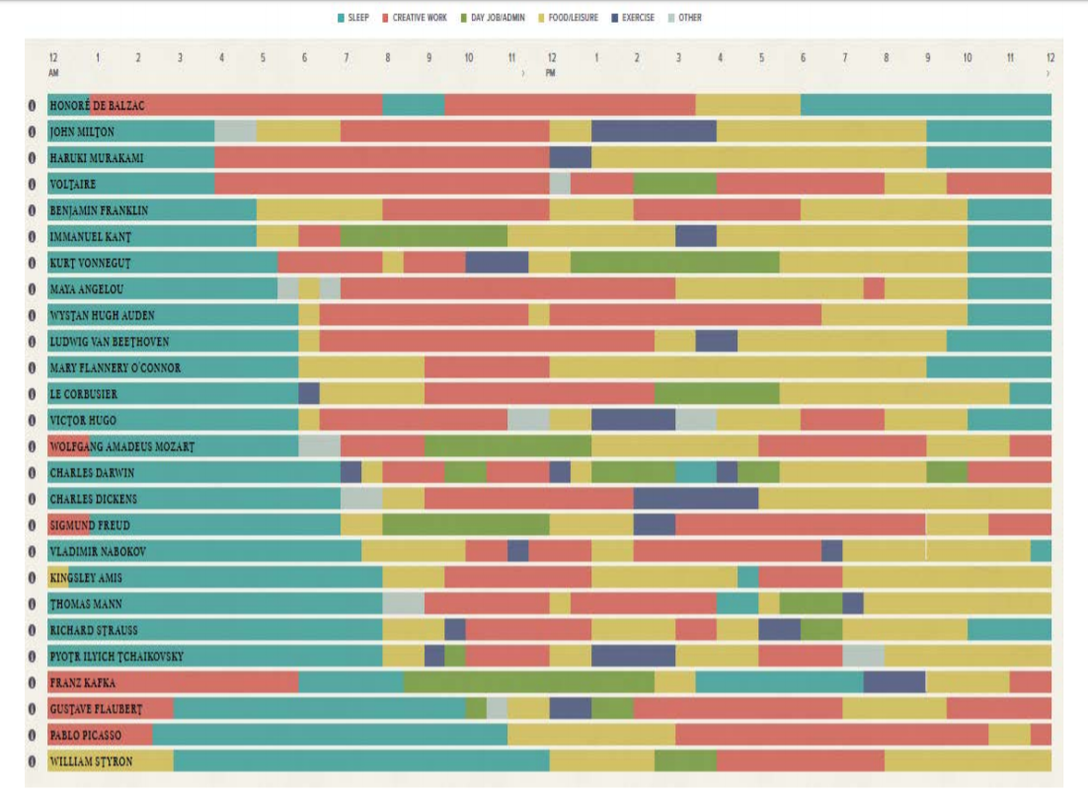
Визуализација на податоци (PDF)
27 април 2020 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) „Визуализацијата ви дава одговори на прашања на кои не сте ни помислиле.“ – Бен Шнеидерман. Постојат многу различни дијаграми за визуализација на податоци, во основна и напредна верзија, нивни варијанти и комбинации, уредени во зависност од тоа што сакаме да потенцираме пред публиката. Визуализацијата е добра, кога е едукативна, дава реално значење на податоците, дава нова перспектива на веќе разгледуван проблем, ја предизвикува имагинацијата и љубопитноста на луѓето. Но, таа исто така може да биде и лоша, да ги искривува информациите и да го одвлекува вниманието од проблемот кој се разгледува. Труд објавен во Математички омнибус 7 (2020). |
|
Нерутински проблеми во наставата по математика во основно образование (PDF)
27 април 2020 во МАТЕМАТИЧКИ ОМНИБУС (НАСТАВА) Една од основните цели на современата настава по математика е да ги оспособи учениците самостојно да решаваат проблеми применувајќи ги стекнатите знаења од предметната област. Наспроти рутинските проблеми чие решавање бара вештини како што се помнењене и разбирање и при тоа се користат веќе познати процедури, нерутинските проблеми бараат вештини како анализа, синтеза и креирање, постапката за нивно решавање не е однапред позната и нудат можност за креативно и иновативно изразување. Труд објавен во Математички омнибус 8 (2020). |
|
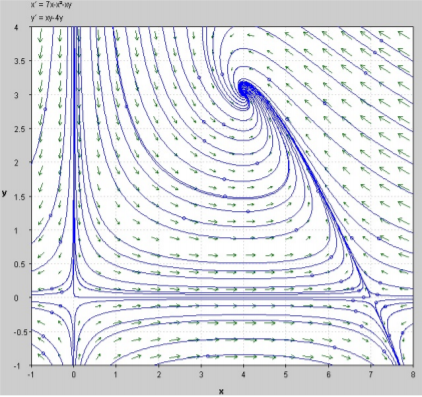
Примена на диференцијални равенки во биологија (PDF)
24 април 2020 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Разгледени се два различни биолошки модели кои се изразуваат преку нелинеарни системи од диференцијални равенки. Тие обично се поедноставни во идеални услови. Од друга страна, во природните процеси тешко може да се предвидат сите надворешни фактори, но сепак овие модели дават доволна индикација дека еколошките модели како и многу други природни појави се стремат кон стабилност. Труд објавен во Математички омнибус 7 (2020). |
|
Златен пресек
20 април 2020 во СТАТИИ ОД МЕСЕЦОТ НА НАУКАТА Пропорција е однос меѓу две величини. Пропорцијата е скриена, но секогаш присутна во композицијата на секое ликовно или архитектонско дело и е еден од одличните чинители на неговата хармонија. Едно од најстарите правила на складноста е пропорцијата наречена златен пресек. Златен пресек е поделба на една отсечка на два дела на тој начин што целата должина спрема големиот дел се однесува исто како поголемиот дел спрема помалиот. Проект презентиран на Ноември - Месец на науката 2019 во категоријата VII-IX одд. |
|
Квадратна фрактална снегулка и квадратна фрактална површина на Кох
06 април 2020 во СТАТИИ ОД МЕСЕЦОТ НА НАУКАТА Голем број тела во природата, како на пример: планините, облаците, дрвјата и слично, се сложени и „неправилни“. Голем број природни тела заради својата сложеност тешко можеле да се претстават математички, сѐ до 1960 год. кога математичарот Benoit Mandelbrot пронашол начин и сложените форми да се проучуваат на систематски начин. Неговото решение се фракталите. Од големиот број фрактали ги избравме геометриските фрактали – квадратна фрактална снегулка на Кох и квадратна фрактална површина на Кох, ги анализиравме нивните страни, плоштини и периметри во секој од чекорите на конструкција. Проект презентиран на Ноември - Месец на науката 2019 во категоријата VII-IX одд. |
|
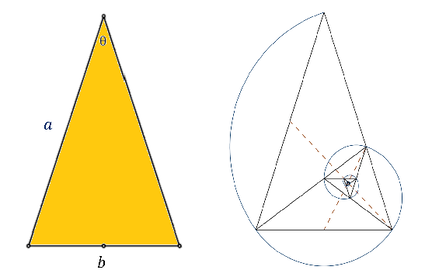
Златни фигури
30 март 2020 во СТАТИИ ОД МЕСЕЦОТ НА НАУКАТА Златни фигури се многуаголници кај кои должините на страните или дијагоналите се во златен сооднос кој приближно изнесува 1:1,618. Златниот правоаголник, ромб и триаголник имаат и други интересни својства. Златните фигури може да се најдат и во мрежите на геометриските тела и кај некои геометриски слики. Проект презентиран на Ноември - Месец на науката 2019 во категоријата VII-IX одд. |
|
Моаре (Moiré) интерферентни геометриски шаблони
23 март 2020 во СТАТИИ ОД МЕСЕЦОТ НА НАУКАТА Зошто шаблоните ги привлекуваат нашите очи? Тие даваат чувство на подреденост и се основа на многу предвидувања. За математиката интересни се геометриските шаблони. Моаре интерферентните шаблони се добиваат кога шаблон со транспарентни празнини се поклопува со ист (или сличен) шаблон. Со ротација на шаблоните се добиваат атрактивни дизајни. Проект презентиран на Ноември - Месец на науката 2019 во категоријата VII-IX одд. |
|
Неколку стратегии за мотивирање на учениците за учење математика (PDF)
22 март 2020 во МАТЕМАТИЧКИ ОМНИБУС (НАСТАВА) Мотивацијата на ученикот за учење ја гради и развива наставникот со своето однесување на наставниот час, со кое дава свое обележје на процесот на реализација на наставната материја. Наставникот може да ја зголеми внатрешната мотивација на ученикот, да ја поттикне неговата жед за знаења и учење. Ученикот треба да учи затоа што тоа го исполнува и радува, а не затоа што тоа некој го очекува од него. Изнаоѓањето на начини за мотивирање на учениците е движечка сила, длабоко вметната во емоционалниот и социјалниот дел од личноста на секој успешен наставник. Труд објавен во Математички омнибус 8 (2020). |
|
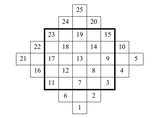
Магични квадрати (PDF)
21 март 2020 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) За историјата на магичните квадрати, нивните општи својства, некои методи за конструирање на магични квадрати, геомагични квадрати, примена на магичните квадрати во наставата по математика и неколку сѐ уште нерешени проблеми за магичните квадрати. Труд објавен во Математички омнибус 7 (2020). |
|
На општо задоволство: Нов тренд во статистичките анализи - тестови за еквиваленција
21 март 2020 во НАУЧНО-ПОПУЛАРНИ СТАТИИ Тестовите за еквиваленција се производи на статистичката теорија на заклучување кои интезивно се развиваат во последните години и кои овозможуваат подобро разбирање на функционирањето на реалниот свет, преку анализа на сличноста, а не на разликите. Овие тестови имаат моќ да ја отстранат пристрасноста на научните резултати, да го намалат бројот, па и да ги елиминираат неточно протолкуваните резултати и со тоа да предизвикаат експанзија на резултати од научните истражувања, „вадејќи ги од фиока“ досегашните „негативни резултати“. Download (PDF) |
|
Пропусти во предзнаењата на студентите и учениците забележани при изучување на предметот математика (PDF)
18 март 2020 во МАТЕМАТИЧКИ ОМНИБУС (НАСТАВА) Надминувањето на проблемите со опаѓање на знаењето по математика и математичките вештини кај учениците и студентите, не е едноставно. Првиот чекор во овој не така лесен процес би требало да биде длабока анализа на потешкотиите на кои наидуваат учениците и студентите, како и пропустите и грешките кои најчесто ги прават при изучување на математиката. Во овој труд се разгледани три вида на грешки при изучување на математиката кои ги прават учениците и студентите: грешки направени од невнимание, грешки во пресметките и концептуални пропусти. Труд објавен во Математички омнибус 8 (2020). |
|
Луда железница и чудни форми од лента
18 март 2020 во СТАТИИ ОД МЕСЕЦОТ НА НАУКАТА Мебиусова лента е површина со една страна и еден раб. Таа може да се добие од парче лента од хартија така што пред да се залепат краевите, на едниот од нив му правиме половина завртување. Има една страна и еден раб, па во тоа е идејата за моделот на Мебиусовата луда железница. Награден проект со втора награда на Ноември - Месец на науката 2019 во категоријата VII-IX год. |
|
Буквите во математичките задачи и формули
4 февруари 2020 во СТАТИИ ОД МЕСЕЦОТ НА НАУКАТА Математиката е дел од нашето секојдневие, а бројките и буквите се основата на нашето образование. Како може да се соединат овие наизглед два сосема спротивни поими (поради тоа што прва асоцијација за буквите се јазиците, а за бројките математиката)? Проект презентиран на Ноември - Месец на науката 2019 во категоријата VII-IX одд. |
|
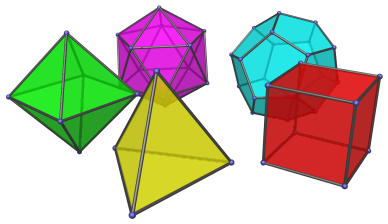
Правилни полиедри - зошто пет?
21 јануари 2020 во СТАТИИ ОД МЕСЕЦОТ НА НАУКАТА Полиедар (или рабесто тело) е фигура ограничена со површини коишто се составени само од многуаголници. За еден конвексен полиедар велиме дека е правилен ако сите негови ѕидови се правилни многуаголници. Постојат само пет правилни полиедри уште познати како Платонови тела. Кои се правилните полиедри и зошто ги има само пет? Награден проект со трета награда на Ноември - Месец на науката 2019 во категоријата VII-IX год. |
|
Визуализација на функции со графичко програмирање
23 декември 2019 во НАУЧНО-ПОПУЛАРНИ СТАТИИ Целта на алатките за визуализациjа на математичките поими е да понудат нов начин на разбирање на тие поими преку интуитивни визуелни прегледи. Во оваа статиjа е обjаснето создавање на едноставна апликациjа за визуализациjа на функции, како и површините добиени со нивна ротациjа околу една оска. Апликацијта користи матрици и својства на операции на матрици со вектори за да се опишат трансформациите во тридимензионален простор - транслација, ротација и скаларно зголемување/намалување. Download (PDF) |
|
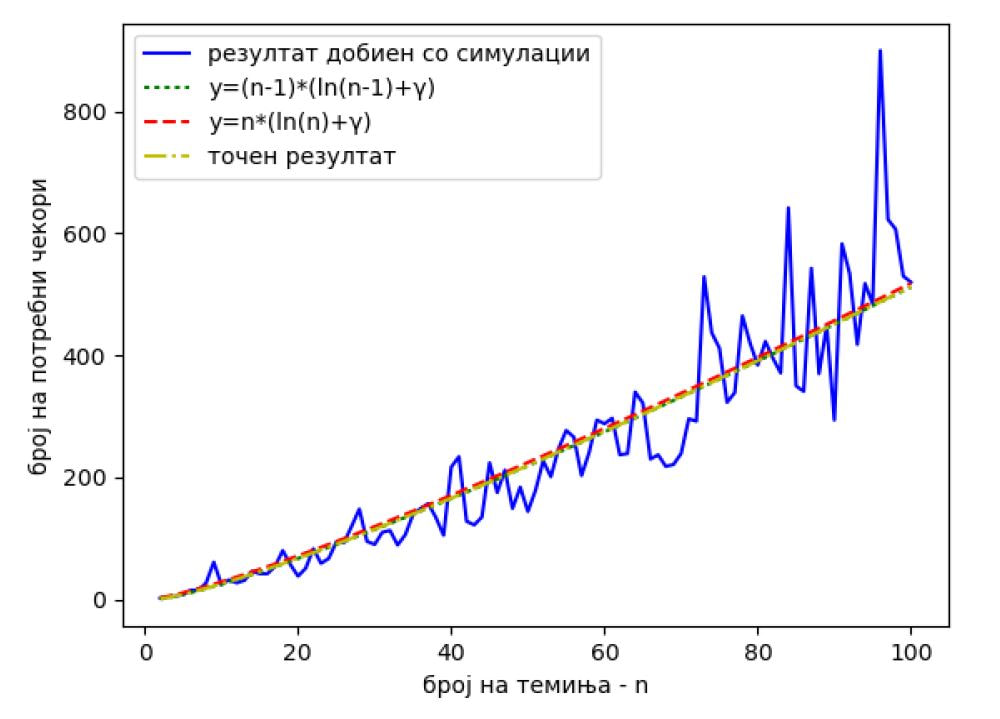
Теорија на графови и задачата на собирање купони (PDF)
11 јуни 2019 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Основната верзија на задачата на собирање купони гласи: Во секоја кутија со житарици има по еден купон кој носи одредена награда, така што постојат r различни видови награди. Еден човек купува по едно пакување од кутијата со житарици, сѐ додека не собере барем по еден награден купон од сите видови награди. Колку кутии со житарици треба да купи човекот? Решението на задачата на собирање купони може да го поистоветиме со очекуваното време за целосно покривање на комплетниот граф. Труд објавен во Математички омнибус 5 (2019). |
|
Докази без зборови
9 јуни 2019 во СТАТИИ ОД МЕСЕЦОТ НА НАУКАТА Доказот без зборови е слика или серија слики кои даваат докази за некое математичко тврдење, т.е. преку набљудување, визуализација и мисловен процес да се сфати и открие пораката на сликата. Изразите „доказ без зборови“ или „визуелен доказ“ ги користиме ако зборуваме за фигура која изразува математички доказ со мало или никакво објаснување. Но, можеме ли доказот без зборови да го сметаме за вистински доказ? Награден експеримент со втора награда на Ноември - Месец на науката 2018 во категоријата I-IV год. |
|
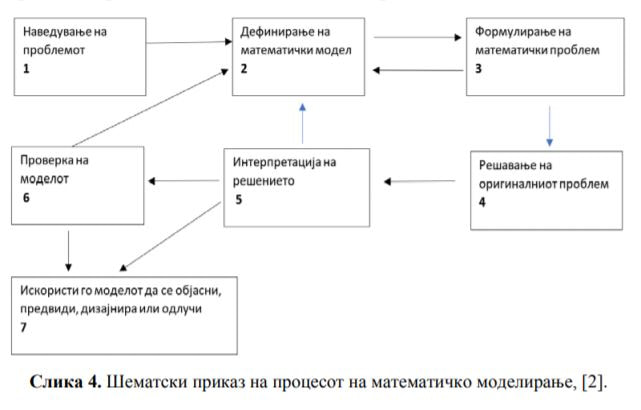
Математичко моделирање и негова примена во наставата по математика (PDF)
7 јуни 2019 во МАТЕМАТИЧКИ ОМНИБУС (НАСТАВА) Математичкото моделирање е процес коj ја користи математиката за да претстави, анализира и да овозможи увид во феномените на реалниот живот. Прашањата за математичко моделирање овозможуваат да истражувате проблеми од секојдневниот живот и со користење на вашите откритија да креирате ново знаење. Сметамe дека штом учениците ќе се стекнат со компетенци за моделирање во училниците, сите останати компетенции ќе следат автоматски. Труд објавен во Математички омнибус 6 (2019). |
|
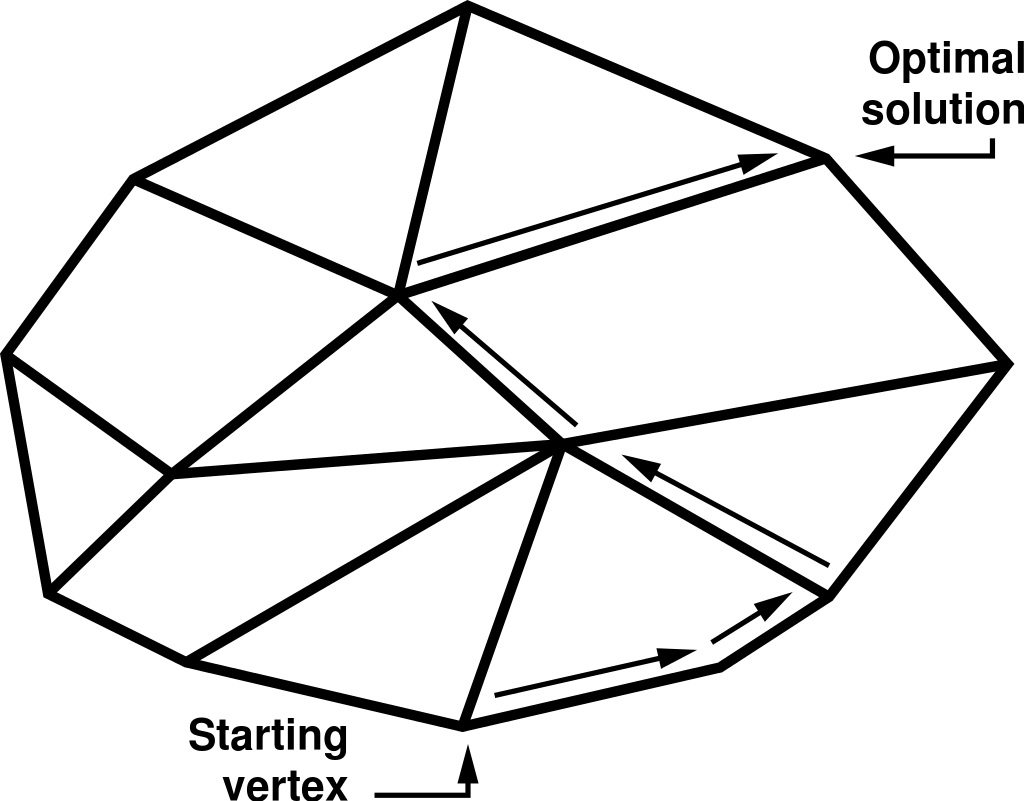
Решавање задачи со симплекс метод во Excel и Mathematica (PDF)
7 јуни 2019 во МАТЕМАТИЧКИ ОМНИБУС (НАСТАВА) Линеарното програмирање е математичко моделирање на практични проблеми со линеарна функција на целта којашто треба да се оптимизира (максимизира или минимизира). Зборот „програмирање“ се однесува на наоѓање на најдобриот (оптимален) план, т.е. одредување на вредности на променливите така што функцијата на целта да добие најдобра (оптимална) вредност при што се задоволени ограничувањата на задачата. Симплекс методот е еден од најпопуларните местоди за решавање на задачи на линерно програмирање. Труд објавен во Математички омнибус 6 (2019). |
|
Шапли-Шубик индекс на моќност - од теорија до секојдневие (PDF)
7 јуни 2019 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Секој од нас се нашол во ситуација да направи избор во одреден момент, односно да се приклучи кон една или друга коалиција, кои застапуваат различни ставови, или поточно кажано се во конфликт. Притоа, важно е определувањето на оптималната стратегија, што може да се изведе со определување на интензитетот на важност на поединецот во групата, односно коалицијата. Труд објавен во Математички омнибус 5 (2019). |
|
Математика во модниот дизајн
6 јуни 2019 во СТАТИИ ОД МЕСЕЦОТ НА НАУКАТА Модните дизајнери употребуваат голем дел од математиката, почнувајќи од наједноставните пресметки и формули, па сѐ до посложени проблеми од аритметика, алгебра, геометрија. Тие се применуваат при дизајнирање фустани со 2Д и 3Д форми, при кроење маици, пантолони и здолништа, при изработка на накит и високи потпетици, при изработка на ткаенини итн. Награден експеримент со прва награда на Ноември - Месец на науката 2018 во категоријата 7-9 одд. |
|
Бинарни квадратни форми (PDF)
5 јуни 2019 во МАТЕМАТИЧКИ ОМНИБУС (НАУКА) Наизглед едноставниот пробем на претставување на прост број како сума од два квадрати бил доволен поттик за формирање на теоријата на Лагранж за редукција на квадратни форми. Оваа теорија не само што целосно ги решава пробелмите на Ферма, туку нуди и алгоритамски пристап кон решавањето на слични проблеми од теоријата на броеви. Труд објавен во Математички омнибус 5 (2019). |
|
Задачи од отворен тип во наставата по математика (PDF)
29 мај 2019 во МАТЕМАТИЧКИ ОМНИБУС (НАСТАВА) За да ги стимулираме учениците да разрешуваат математички проблеми, неопходно е да ги замениме задачите од затворен, со задачи од отворен тип. Односно, неопходно е барањата на наставникот, учениците да: пресметаат, ре-шат, одредат и да применат алгоритам, да ги замениме со барања, учениците да увидат, размислат, поврзат, препознаат математички елементи и да образложат. Труд објавен во Математички омнибус 6 (2019). |